Regression with Sensor Data Containing Incomplete Observations

This paper addresses a regression problem in which output label values are the results of sensing the magnitude of a phenomenon. A low value of such labels can mean either that the actual magnitude of the phenomenon was low or that the sensor made an incomplete observation. This leads to a bias toward lower values in labels and its resultant learning because labels may have lower values due to incomplete observations, even if the actual magnitude of the phenomenon was high. Moreover, because an incomplete observation does not provide any tags indicating incompleteness, we cannot eliminate or impute them. To address this issue, we propose a learning algorithm that explicitly models incomplete observations corrupted with an asymmetric noise that always has a negative value. We show that our algorithm is unbiased as if it were learned from uncorrupted data that does not involve incomplete observations. We demonstrate the advantages of our algorithm through numerical experiments.

Cumulative Stay-time Representation for Electronic Health Records in Medical Event Time Prediction

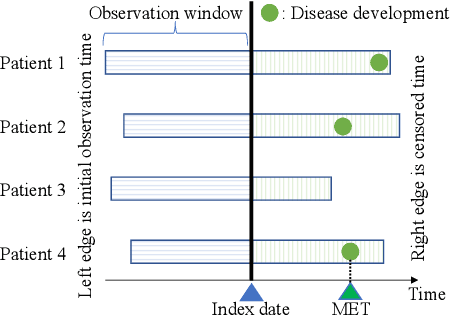
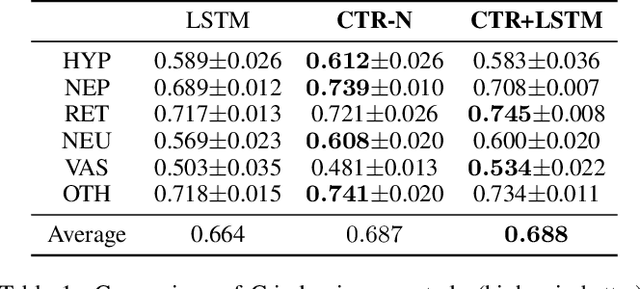
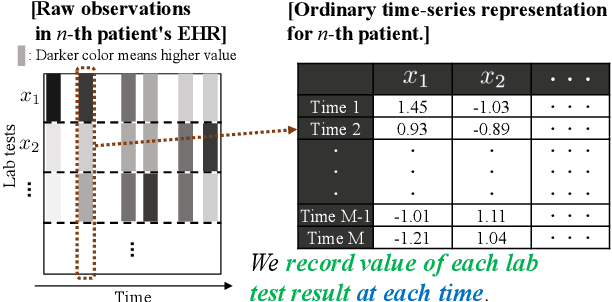
We address the problem of predicting when a disease will develop, i.e., medical event time (MET), from a patient's electronic health record (EHR). The MET of non-communicable diseases like diabetes is highly correlated to cumulative health conditions, more specifically, how much time the patient spent with specific health conditions in the past. The common time-series representation is indirect in extracting such information from EHR because it focuses on detailed dependencies between values in successive observations, not cumulative information. We propose a novel data representation for EHR called cumulative stay-time representation (CTR), which directly models such cumulative health conditions. We derive a trainable construction of CTR based on neural networks that has the flexibility to fit the target data and scalability to handle high-dimensional EHR. Numerical experiments using synthetic and real-world datasets demonstrate that CTR alone achieves a high prediction performance, and it enhances the performance of existing models when combined with them.

Learning to Estimate Driver Drowsiness from Car Acceleration Sensors using Weakly Labeled Data

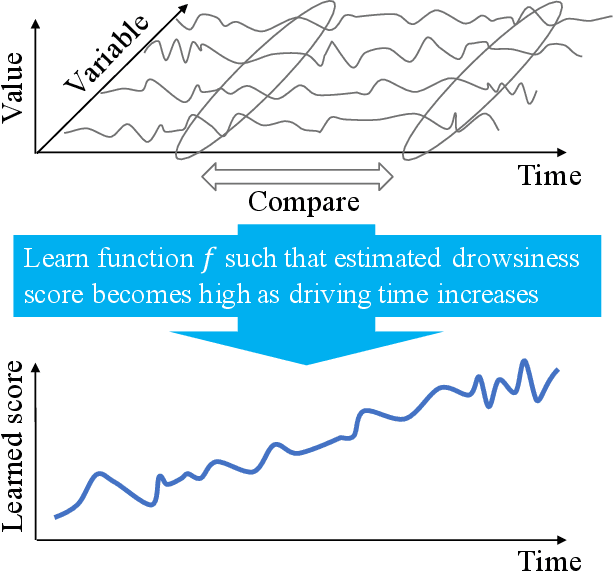
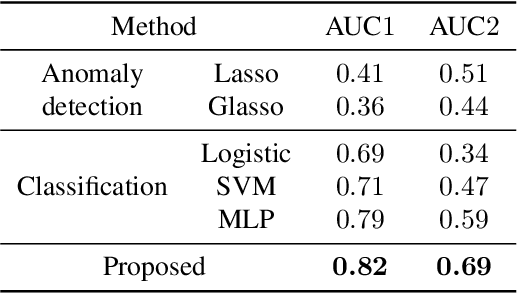
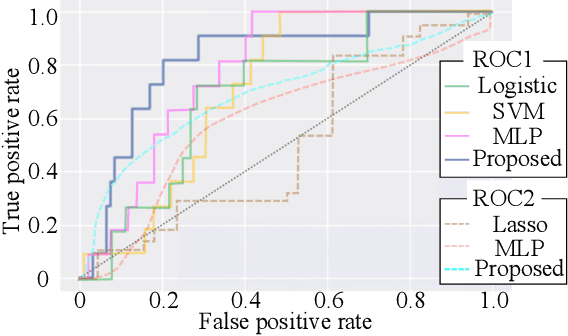
This paper addresses the learning task of estimating driver drowsiness from the signals of car acceleration sensors. Since even drivers themselves cannot perceive their own drowsiness in a timely manner unless they use burdensome invasive sensors, obtaining labeled training data for each timestamp is not a realistic goal. To deal with this difficulty, we formulate the task as a weakly supervised learning. We only need to add labels for each complete trip, not for every timestamp independently. By assuming that some aspects of driver drowsiness increase over time due to tiredness, we formulate an algorithm that can learn from such weakly labeled data. We derive a scalable stochastic optimization method as a way of implementing the algorithm. Numerical experiments on real driving datasets demonstrate the advantages of our algorithm against baseline methods.

Time-Discounting Convolution for Event Sequences with Ambiguous Timestamps

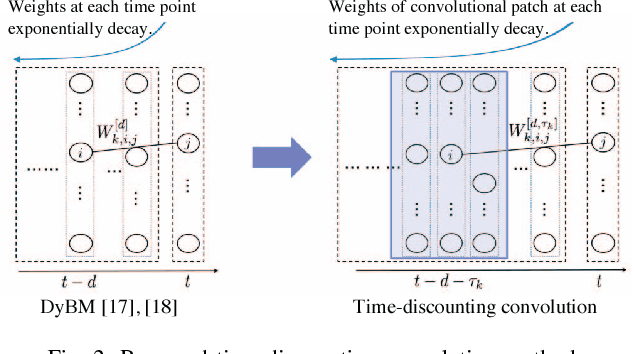
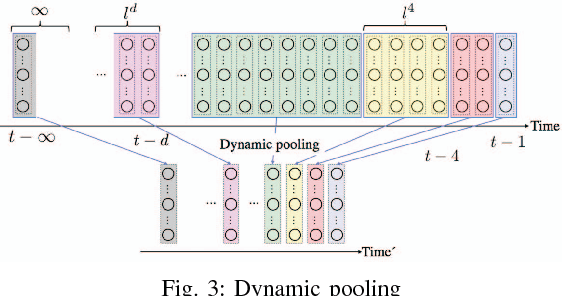
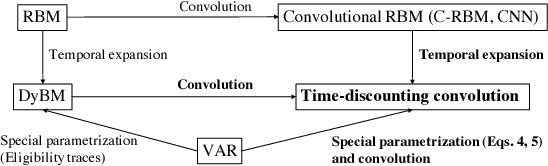
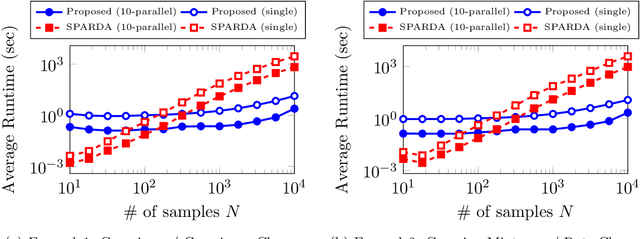
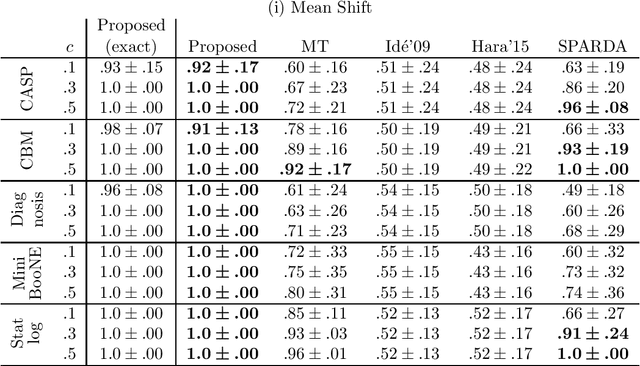
This paper proposes a method for modeling event sequences with ambiguous timestamps, a time-discounting convolution. Unlike in ordinary time series, time intervals are not constant, small time-shifts have no significant effect, and inputting timestamps or time durations into a model is not effective. The criteria that we require for the modeling are providing robustness against time-shifts or timestamps uncertainty as well as maintaining the essential capabilities of time-series models, i.e., forgetting meaningless past information and handling infinite sequences. The proposed method handles them with a convolutional mechanism across time with specific parameterizations, which efficiently represents the event dependencies in a time-shift invariant manner while discounting the effect of past events, and a dynamic pooling mechanism, which provides robustness against the uncertainty in timestamps and enhances the time-discounting capability by dynamically changing the pooling window size. In our learning algorithm, the decaying and dynamic pooling mechanisms play critical roles in handling infinite and variable length sequences. Numerical experiments on real-world event sequences with ambiguous timestamps and ordinary time series demonstrated the advantages of our method.

Consistent Nonparametric Different-Feature Selection via the Sparsest $k$-Subgraph Problem

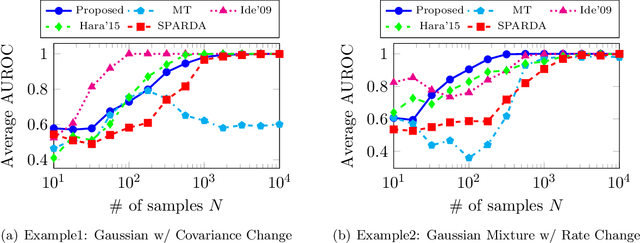
Two-sample feature selection is the problem of finding features that describe a difference between two probability distributions, which is a ubiquitous problem in both scientific and engineering studies. However, existing methods have limited applicability because of their restrictive assumptions on data distributoins or computational difficulty. In this paper, we resolve these difficulties by formulating the problem as a sparsest $k$-subgraph problem. The proposed method is nonparametric and does not assume any specific parametric models on the data distributions. We show that the proposed method is computationally efficient and does not require any extra computation for model selection. Moreover, we prove that the proposed method provides a consistent estimator of features under mild conditions. Our experimental results show that the proposed method outperforms the current method with regard to both accuracy and computation time.

Posterior Mean Super-resolution with a Causal Gaussian Markov Random Field Prior

We propose a Bayesian image super-resolution (SR) method with a causal Gaussian Markov random field (MRF) prior. SR is a technique to estimate a spatially high-resolution image from given multiple low-resolution images. An MRF model with the line process supplies a preferable prior for natural images with edges. We improve the existing image transformation model, the compound MRF model, and its hyperparameter prior model. We also derive the optimal estimator -- not the joint maximum a posteriori (MAP) or marginalized maximum likelihood (ML), but the posterior mean (PM) -- from the objective function of the L2-norm (mean square error) -based peak signal-to-noise ratio (PSNR). Point estimates such as MAP and ML are generally not stable in ill-posed high-dimensional problems because of overfitting, while PM is a stable estimator because all the parameters in the model are evaluated as distributions. The estimator is numerically determined by using variational Bayes. Variational Bayes is a widely used method that approximately determines a complicated posterior distribution, but it is generally hard to use because it needs the conjugate prior. We solve this problem with simple Taylor approximations. Experimental results have shown that the proposed method is more accurate or comparable to existing methods.

Posterior Mean Super-Resolution with a Compound Gaussian Markov Random Field Prior

This manuscript proposes a posterior mean (PM) super-resolution (SR) method with a compound Gaussian Markov random field (MRF) prior. SR is a technique to estimate a spatially high-resolution image from observed multiple low-resolution images. A compound Gaussian MRF model provides a preferable prior for natural images that preserves edges. PM is the optimal estimator for the objective function of peak signal-to-noise ratio (PSNR). This estimator is numerically determined by using variational Bayes (VB). We then solve the conjugate prior problem on VB and the exponential-order calculation cost problem of a compound Gaussian MRF prior with simple Taylor approximations. In experiments, the proposed method roughly overcomes existing methods.