Foundation of Calculating Normalized Maximum Likelihood for Continuous Probability Models

The normalized maximum likelihood (NML) code length is widely used as a model selection criterion based on the minimum description length principle, where the model with the shortest NML code length is selected. A common method to calculate the NML code length is to use the sum (for a discrete model) or integral (for a continuous model) of a function defined by the distribution of the maximum likelihood estimator. While this method has been proven to correctly calculate the NML code length of discrete models, no proof has been provided for continuous cases. Consequently, it has remained unclear whether the method can accurately calculate the NML code length of continuous models. In this paper, we solve this problem affirmatively, proving that the method is also correct for continuous cases. Remarkably, completing the proof for continuous cases is non-trivial in that it cannot be achieved by merely replacing the sums in discrete cases with integrals, as the decomposition trick applied to sums in the discrete model case proof is not applicable to integrals in the continuous model case proof. To overcome this, we introduce a novel decomposition approach based on the coarea formula from geometric measure theory, which is essential to establishing our proof for continuous cases.

Extrinsic Calibration of Multiple LiDARs for a Mobile Robot based on Floor Plane And Object Segmentation

Mobile robots equipped with multiple light detection and ranging (LiDARs) and capable of recognizing their surroundings are increasing due to the minitualization and cost reduction of LiDAR. This paper proposes a target-less extrinsic calibration method of multiple LiDARs with non-overlapping field of view (FoV). The proposed method uses accumulated point clouds of floor plane and objects while in motion. It enables accurate calibration with challenging configuration of LiDARs that directed towards the floor plane, caused by biased feature values. Additionally, the method includes a noise removal module that considers the scanning pattern to address bleeding points, which are noises of significant source of error in point cloud alignment using high-density LiDARs. Evaluations through simulation demonstrate that the proposed method achieved higher accuracy extrinsic calibration with two and four LiDARs than conventional methods, regardless type of objects. Furthermore, the experiments using a real mobile robot has shown that our proposed noise removal module can eliminate noise more precisely than conventional methods, and the estimated extrinsic parameters have successfully created consistent 3D maps.

Tight and fast generalization error bound of graph embedding in metric space

Recent studies have experimentally shown that we can achieve in non-Euclidean metric space effective and efficient graph embedding, which aims to obtain the vertices' representations reflecting the graph's structure in the metric space. Specifically, graph embedding in hyperbolic space has experimentally succeeded in embedding graphs with hierarchical-tree structure, e.g., data in natural languages, social networks, and knowledge bases. However, recent theoretical analyses have shown a much higher upper bound on non-Euclidean graph embedding's generalization error than Euclidean one's, where a high generalization error indicates that the incompleteness and noise in the data can significantly damage learning performance. It implies that the existing bound cannot guarantee the success of graph embedding in non-Euclidean metric space in a practical training data size, which can prevent non-Euclidean graph embedding's application in real problems. This paper provides a novel upper bound of graph embedding's generalization error by evaluating the local Rademacher complexity of the model as a function set of the distances of representation couples. Our bound clarifies that the performance of graph embedding in non-Euclidean metric space, including hyperbolic space, is better than the existing upper bounds suggest. Specifically, our new upper bound is polynomial in the metric space's geometric radius $R$ and can be $O(\frac{1}{S})$ at the fastest, where $S$ is the training data size. Our bound is significantly tighter and faster than the existing one, which can be exponential to $R$ and $O(\frac{1}{\sqrt{S}})$ at the fastest. Specific calculations on example cases show that graph embedding in non-Euclidean metric space can outperform that in Euclidean space with much smaller training data than the existing bound has suggested.

Cumulative Stay-time Representation for Electronic Health Records in Medical Event Time Prediction

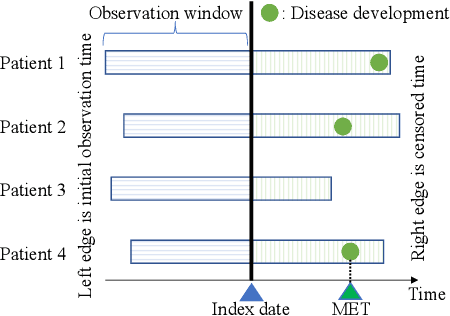
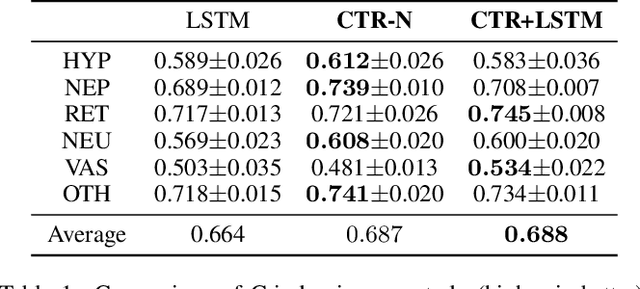
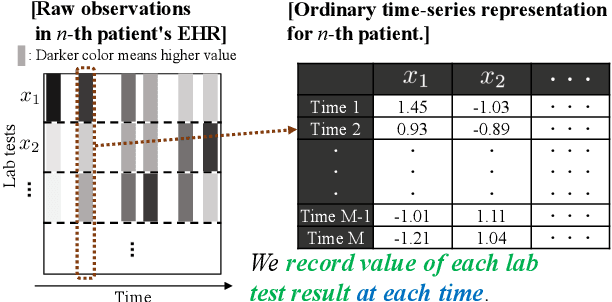
We address the problem of predicting when a disease will develop, i.e., medical event time (MET), from a patient's electronic health record (EHR). The MET of non-communicable diseases like diabetes is highly correlated to cumulative health conditions, more specifically, how much time the patient spent with specific health conditions in the past. The common time-series representation is indirect in extracting such information from EHR because it focuses on detailed dependencies between values in successive observations, not cumulative information. We propose a novel data representation for EHR called cumulative stay-time representation (CTR), which directly models such cumulative health conditions. We derive a trainable construction of CTR based on neural networks that has the flexibility to fit the target data and scalability to handle high-dimensional EHR. Numerical experiments using synthetic and real-world datasets demonstrate that CTR alone achieves a high prediction performance, and it enhances the performance of existing models when combined with them.

Generalization Error Bound for Hyperbolic Ordinal Embedding

Hyperbolic ordinal embedding (HOE) represents entities as points in hyperbolic space so that they agree as well as possible with given constraints in the form of entity i is more similar to entity j than to entity k. It has been experimentally shown that HOE can obtain representations of hierarchical data such as a knowledge base and a citation network effectively, owing to hyperbolic space's exponential growth property. However, its theoretical analysis has been limited to ideal noiseless settings, and its generalization error in compensation for hyperbolic space's exponential representation ability has not been guaranteed. The difficulty is that existing generalization error bound derivations for ordinal embedding based on the Gramian matrix do not work in HOE, since hyperbolic space is not inner-product space. In this paper, through our novel characterization of HOE with decomposed Lorentz Gramian matrices, we provide a generalization error bound of HOE for the first time, which is at most exponential with respect to the embedding space's radius. Our comparison between the bounds of HOE and Euclidean ordinal embedding shows that HOE's generalization error is reasonable as a cost for its exponential representation ability.

Time-Discounting Convolution for Event Sequences with Ambiguous Timestamps

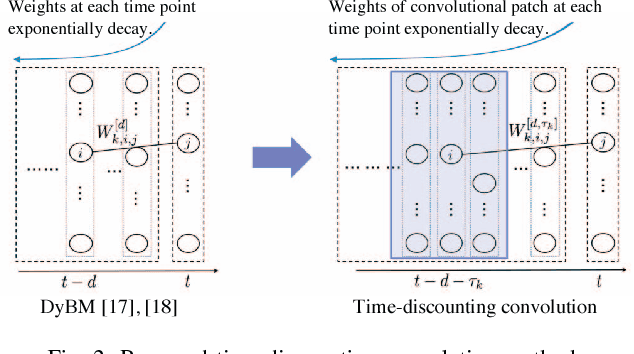
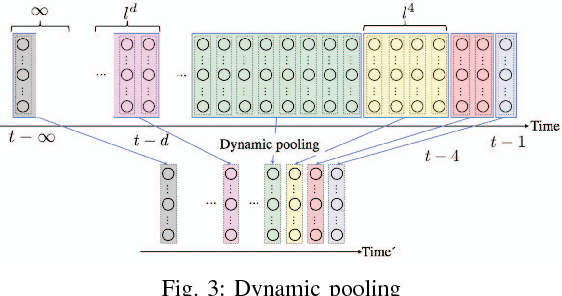
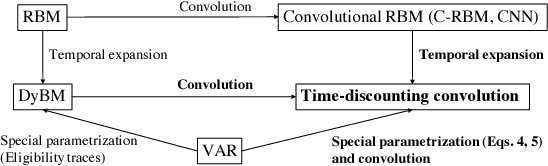
This paper proposes a method for modeling event sequences with ambiguous timestamps, a time-discounting convolution. Unlike in ordinary time series, time intervals are not constant, small time-shifts have no significant effect, and inputting timestamps or time durations into a model is not effective. The criteria that we require for the modeling are providing robustness against time-shifts or timestamps uncertainty as well as maintaining the essential capabilities of time-series models, i.e., forgetting meaningless past information and handling infinite sequences. The proposed method handles them with a convolutional mechanism across time with specific parameterizations, which efficiently represents the event dependencies in a time-shift invariant manner while discounting the effect of past events, and a dynamic pooling mechanism, which provides robustness against the uncertainty in timestamps and enhances the time-discounting capability by dynamically changing the pooling window size. In our learning algorithm, the decaying and dynamic pooling mechanisms play critical roles in handling infinite and variable length sequences. Numerical experiments on real-world event sequences with ambiguous timestamps and ordinary time series demonstrated the advantages of our method.

Stable Geodesic Update on Hyperbolic Space and its Application to Poincare Embeddings

A hyperbolic space has been shown to be more capable of modeling complex networks than a Euclidean space. This paper proposes an explicit update rule along geodesics in a hyperbolic space. The convergence of our algorithm is theoretically guaranteed, and the convergence rate is better than the conventional Euclidean gradient descent algorithm. Moreover, our algorithm avoids the "bias" problem of existing methods using the Riemannian gradient. Experimental results demonstrate the good performance of our algorithm in the \Poincare embeddings of knowledge base data.