BMFM-RNA: An Open Framework for Building and Evaluating Transcriptomic Foundation Models

Transcriptomic foundation models (TFMs) have recently emerged as powerful tools for analyzing gene expression in cells and tissues, supporting key tasks such as cell-type annotation, batch correction, and perturbation prediction. However, the diversity of model implementations and training strategies across recent TFMs, though promising, makes it challenging to isolate the contribution of individual design choices or evaluate their potential synergies. This hinders the field's ability to converge on best practices and limits the reproducibility of insights across studies. We present BMFM-RNA, an open-source, modular software package that unifies diverse TFM pretraining and fine-tuning objectives within a single framework. Leveraging this capability, we introduce a novel training objective, whole cell expression decoder (WCED), which captures global expression patterns using an autoencoder-like CLS bottleneck representation. In this paper, we describe the framework, supported input representations, and training objectives. We evaluated four model checkpoints pretrained on CELLxGENE using combinations of masked language modeling (MLM), WCED and multitask learning. Using the benchmarking capabilities of BMFM-RNA, we show that WCED-based models achieve performance that matches or exceeds state-of-the-art approaches like scGPT across more than a dozen datasets in both zero-shot and fine-tuning tasks. BMFM-RNA, available as part of the biomed-multi-omics project ( https://github.com/BiomedSciAI/biomed-multi-omic ), offers a reproducible foundation for systematic benchmarking and community-driven exploration of optimal TFM training strategies, enabling the development of more effective tools to leverage the latest advances in AI for understanding cell biology.

Cumulative Stay-time Representation for Electronic Health Records in Medical Event Time Prediction

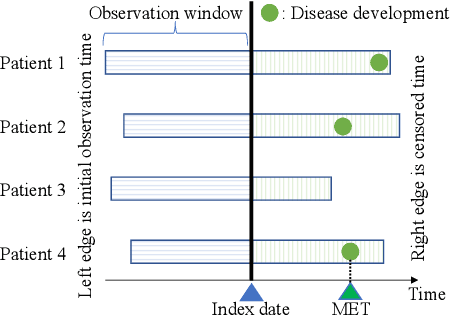
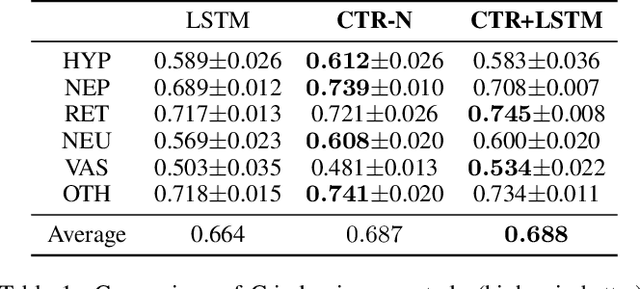
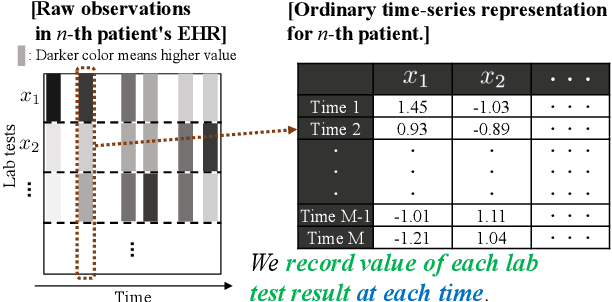
We address the problem of predicting when a disease will develop, i.e., medical event time (MET), from a patient's electronic health record (EHR). The MET of non-communicable diseases like diabetes is highly correlated to cumulative health conditions, more specifically, how much time the patient spent with specific health conditions in the past. The common time-series representation is indirect in extracting such information from EHR because it focuses on detailed dependencies between values in successive observations, not cumulative information. We propose a novel data representation for EHR called cumulative stay-time representation (CTR), which directly models such cumulative health conditions. We derive a trainable construction of CTR based on neural networks that has the flexibility to fit the target data and scalability to handle high-dimensional EHR. Numerical experiments using synthetic and real-world datasets demonstrate that CTR alone achieves a high prediction performance, and it enhances the performance of existing models when combined with them.

Time-Discounting Convolution for Event Sequences with Ambiguous Timestamps

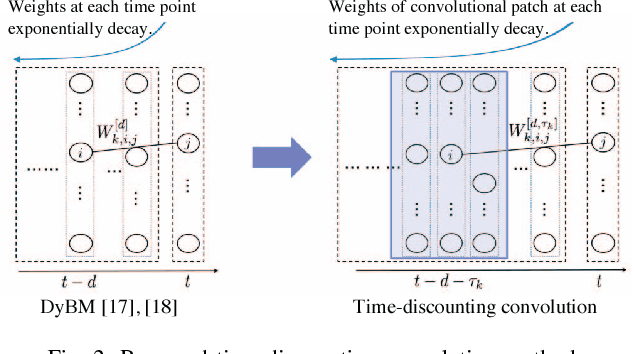
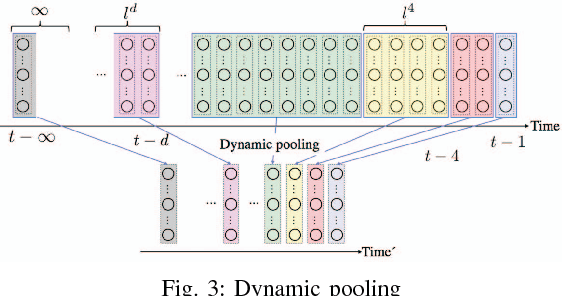
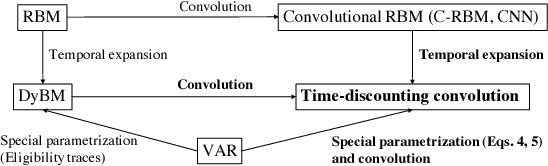
This paper proposes a method for modeling event sequences with ambiguous timestamps, a time-discounting convolution. Unlike in ordinary time series, time intervals are not constant, small time-shifts have no significant effect, and inputting timestamps or time durations into a model is not effective. The criteria that we require for the modeling are providing robustness against time-shifts or timestamps uncertainty as well as maintaining the essential capabilities of time-series models, i.e., forgetting meaningless past information and handling infinite sequences. The proposed method handles them with a convolutional mechanism across time with specific parameterizations, which efficiently represents the event dependencies in a time-shift invariant manner while discounting the effect of past events, and a dynamic pooling mechanism, which provides robustness against the uncertainty in timestamps and enhances the time-discounting capability by dynamically changing the pooling window size. In our learning algorithm, the decaying and dynamic pooling mechanisms play critical roles in handling infinite and variable length sequences. Numerical experiments on real-world event sequences with ambiguous timestamps and ordinary time series demonstrated the advantages of our method.