Mechanism design with multi-armed bandit

A popular approach of automated mechanism design is to formulate a linear program (LP) whose solution gives a mechanism with desired properties. We analytically derive a class of optimal solutions for such an LP that gives mechanisms achieving standard properties of efficiency, incentive compatibility, strong budget balance (SBB), and individual rationality (IR), where SBB and IR are satisfied in expectation. Notably, our solutions are represented by an exponentially smaller number of essential variables than the original variables of LP. Our solutions, however, involve a term whose exact evaluation requires solving a certain optimization problem exponentially many times as the number of players, $N$, grows. We thus evaluate this term by modeling it as the problem of estimating the mean reward of the best arm in multi-armed bandit (MAB), propose a Probably and Approximately Correct estimator, and prove its asymptotic optimality by establishing a lower bound on its sample complexity. This MAB approach reduces the number of times the optimization problem is solved from exponential to $O(N\,\log N)$. Numerical experiments show that the proposed approach finds mechanisms that are guaranteed to achieve desired properties with high probability for environments with up to 128 players, which substantially improves upon the prior work.

Regression with Sensor Data Containing Incomplete Observations

This paper addresses a regression problem in which output label values are the results of sensing the magnitude of a phenomenon. A low value of such labels can mean either that the actual magnitude of the phenomenon was low or that the sensor made an incomplete observation. This leads to a bias toward lower values in labels and its resultant learning because labels may have lower values due to incomplete observations, even if the actual magnitude of the phenomenon was high. Moreover, because an incomplete observation does not provide any tags indicating incompleteness, we cannot eliminate or impute them. To address this issue, we propose a learning algorithm that explicitly models incomplete observations corrupted with an asymmetric noise that always has a negative value. We show that our algorithm is unbiased as if it were learned from uncorrupted data that does not involve incomplete observations. We demonstrate the advantages of our algorithm through numerical experiments.

Online Learning in Supply-Chain Games

We study a repeated game between a supplier and a retailer who want to maximize their respective profits without full knowledge of the problem parameters. After characterizing the uniqueness of the Stackelberg equilibrium of the stage game with complete information, we show that even with partial knowledge of the joint distribution of demand and production costs, natural learning dynamics guarantee convergence of the joint strategy profile of supplier and retailer to the Stackelberg equilibrium of the stage game. We also prove finite-time bounds on the supplier's regret and asymptotic bounds on the retailer's regret, where the specific rates depend on the type of knowledge preliminarily available to the players. In the special case when the supplier is not strategic (vertical integration), we prove optimal finite-time regret bounds on the retailer's regret (or, equivalently, the social welfare) when costs and demand are adversarially generated and the demand is censored.

Biases in In Silico Evaluation of Molecular Optimization Methods and Bias-Reduced Evaluation Methodology

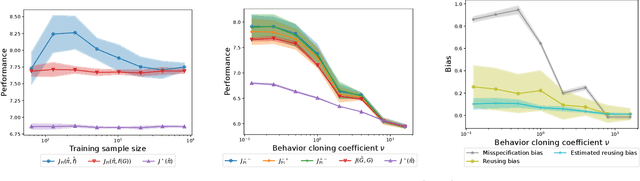
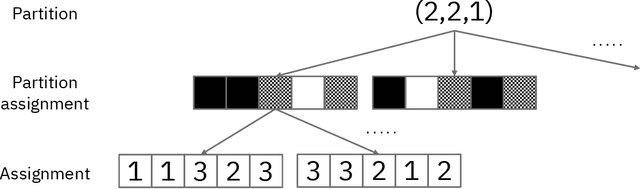
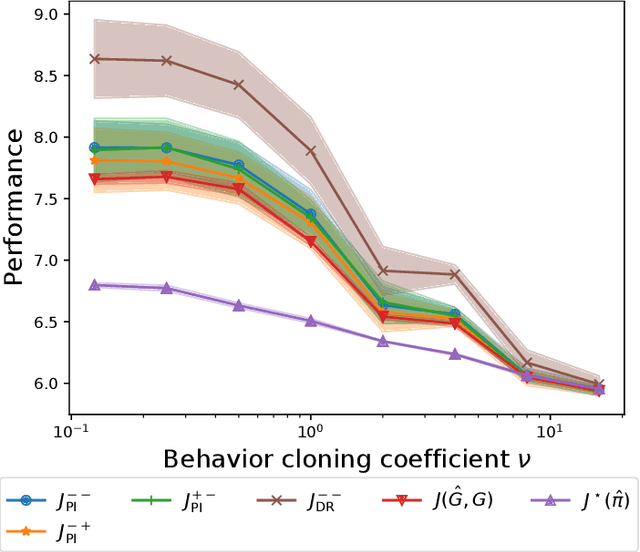
We are interested in in silico evaluation methodology for molecular optimization methods. Given a sample of molecules and their properties of our interest, we wish not only to train an agent that can find molecules optimized with respect to the target property but also to evaluate its performance. A common practice is to train a predictor of the target property on the sample and use it for both training and evaluating the agent. We show that this evaluator potentially suffers from two biases; one is due to misspecification of the predictor and the other to reusing the same sample for training and evaluation. We discuss bias reduction methods for each of the biases comprehensively, and empirically investigate their effectiveness.

Proofs and additional experiments on Second order techniques for learning time-series with structural breaks

We provide complete proofs of the lemmas about the properties of the regularized loss function that is used in the second order techniques for learning time-series with structural breaks in Osogami (2021). In addition, we show experimental results that support the validity of the techniques.

Supplementary material for Uncorrected least-squares temporal difference with lambda-return

Here, we provide a supplementary material for Takayuki Osogami, "Uncorrected least-squares temporal difference with lambda-return," which appears in {\it Proceedings of the 34th AAAI Conference on Artificial Intelligence} (AAAI-20).

Visual analytics for team-based invasion sports with significant events and Markov reward process

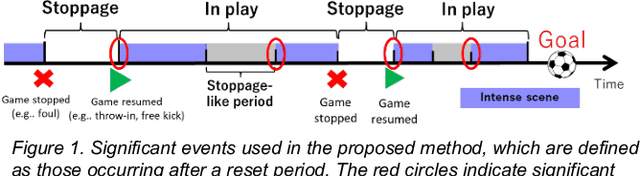
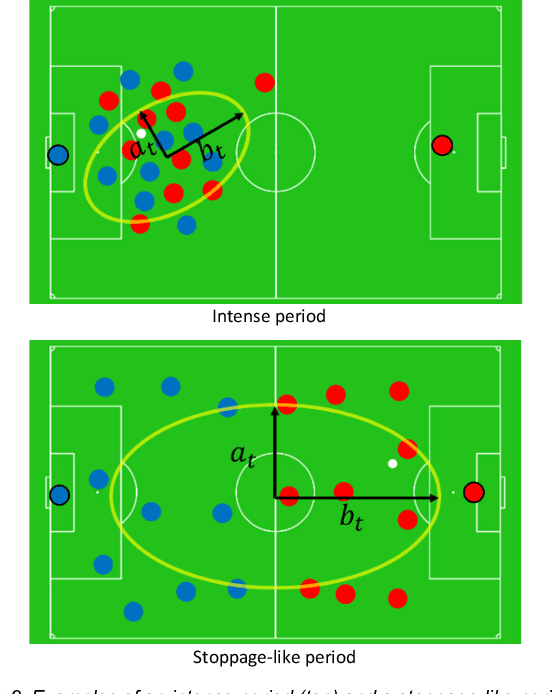
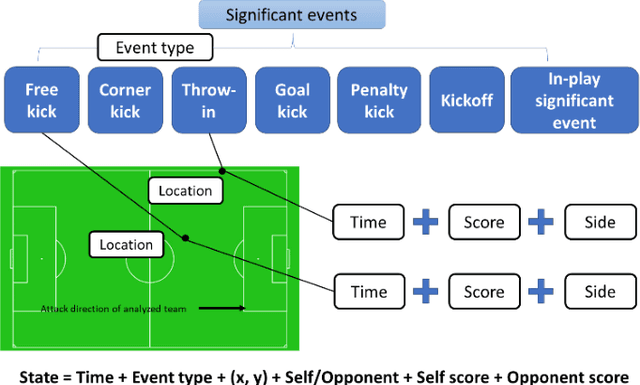
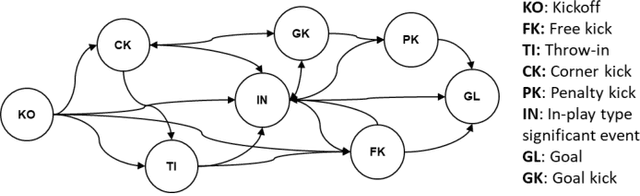
In team-based invasion sports such as soccer and basketball, analytics is important for teams to understand their performance and for audiences to understand matches better. The present work focuses on performing visual analytics to evaluate the value of any kind of event occurring in a sports match with a continuous parameter space. Here, the continuous parameter space involves the time, location, score, and other parameters. Because the spatiotemporal data used in such analytics is a low-level representation and has a very large size, however, traditional analytics may need to discretize the continuous parameter space (e.g., subdivide the playing area) or use a local feature to limit the analysis to specific events (e.g., only shots). These approaches make evaluation impossible for any kind of event with a continuous parameter space. To solve this problem, we consider a whole match as a Markov chain of significant events, so that event values can be estimated with a continuous parameter space by solving the Markov chain with a machine learning model. The significant events are first extracted by considering the time-varying distribution of players to represent the whole match. Then, the extracted events are redefined as different states with the continuous parameter space and built as a Markov chain so that a Markov reward process can be applied. Finally, the Markov reward process is solved by a customized fitted-value iteration algorithm so that the event values with the continuous parameter space can be predicted by a regression model. As a result, the event values can be visually inspected over the whole playing field under arbitrary given conditions. Experimental results with real soccer data show the effectiveness of the proposed system.

Real-time tree search with pessimistic scenarios

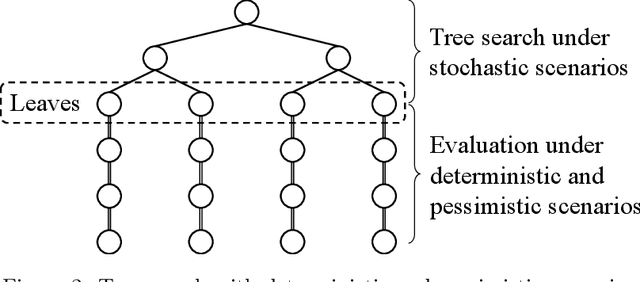
Autonomous agents need to make decisions in a sequential manner, under partially observable environment, and in consideration of how other agents behave. In critical situations, such decisions need to be made in real time for example to avoid collisions and recover to safe conditions. We propose a technique of tree search where a deterministic and pessimistic scenario is used after a specified depth. Because there is no branching with the deterministic scenario, the proposed technique allows us to take into account far ahead in the future in real time. The effectiveness of the proposed technique is demonstrated in Pommerman, a multi-agent environment used in a NeurIPS 2018 competition, where the agents that implement the proposed technique have won the first and third places.

Time-Discounting Convolution for Event Sequences with Ambiguous Timestamps

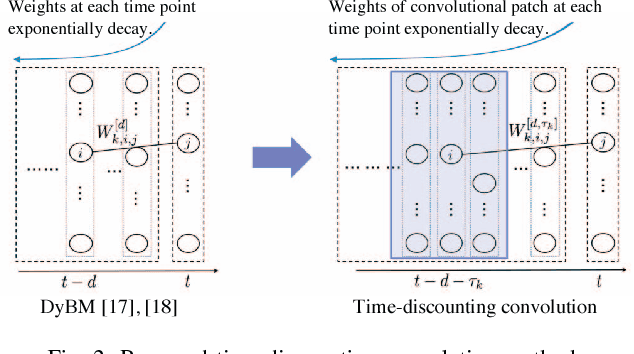
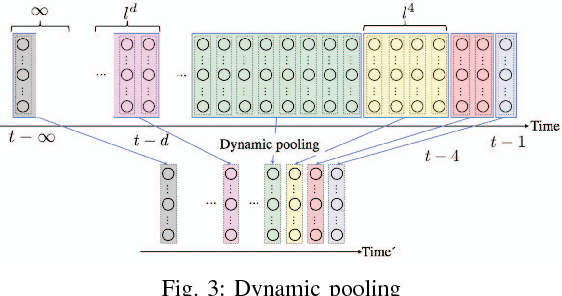
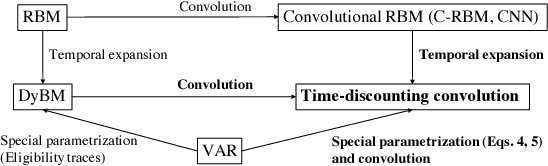
This paper proposes a method for modeling event sequences with ambiguous timestamps, a time-discounting convolution. Unlike in ordinary time series, time intervals are not constant, small time-shifts have no significant effect, and inputting timestamps or time durations into a model is not effective. The criteria that we require for the modeling are providing robustness against time-shifts or timestamps uncertainty as well as maintaining the essential capabilities of time-series models, i.e., forgetting meaningless past information and handling infinite sequences. The proposed method handles them with a convolutional mechanism across time with specific parameterizations, which efficiently represents the event dependencies in a time-shift invariant manner while discounting the effect of past events, and a dynamic pooling mechanism, which provides robustness against the uncertainty in timestamps and enhances the time-discounting capability by dynamically changing the pooling window size. In our learning algorithm, the decaying and dynamic pooling mechanisms play critical roles in handling infinite and variable length sequences. Numerical experiments on real-world event sequences with ambiguous timestamps and ordinary time series demonstrated the advantages of our method.

Dynamic Boltzmann Machines for Second Order Moments and Generalized Gaussian Distributions

Dynamic Boltzmann Machine (DyBM) has been shown highly efficient to predict time-series data. Gaussian DyBM is a DyBM that assumes the predicted data is generated by a Gaussian distribution whose first-order moment (mean) dynamically changes over time but its second-order moment (variance) is fixed. However, in many financial applications, the assumption is quite limiting in two aspects. First, even when the data follows a Gaussian distribution, its variance may change over time. Such variance is also related to important temporal economic indicators such as the market volatility. Second, financial time-series data often requires learning datasets generated by the generalized Gaussian distribution with an additional shape parameter that is important to approximate heavy-tailed distributions. Addressing those aspects, we show how to extend DyBM that results in significant performance improvement in predicting financial time-series data.