Sequence-Aware Inline Measurement Attribution for Good-Bad Wafer Diagnosis

How can we identify problematic upstream processes when a certain type of wafer defect starts appearing at a quality checkpoint? Given the complexity of modern semiconductor manufacturing, which involves thousands of process steps, cross-process root cause analysis for wafer defects has been considered highly challenging. This paper proposes a novel framework called Trajectory Shapley Attribution (TSA), an extension of Shapley values (SV), a widely used attribution algorithm in explainable artificial intelligence research. TSA overcomes key limitations of standard SV, including its disregard for the sequential nature of manufacturing processes and its reliance on an arbitrarily chosen reference point. We applied TSA to a good-bad wafer diagnosis task in experimental front-end-of-line processes at the NY CREATES Albany NanoTech fab, aiming to identify measurement items (serving as proxies for process parameters) most relevant to abnormal defect occurrence.

Wafer Defect Root Cause Analysis with Partial Trajectory Regression

Identifying upstream processes responsible for wafer defects is challenging due to the combinatorial nature of process flows and the inherent variability in processing routes, which arises from factors such as rework operations and random process waiting times. This paper presents a novel framework for wafer defect root cause analysis, called Partial Trajectory Regression (PTR). The proposed framework is carefully designed to address the limitations of conventional vector-based regression models, particularly in handling variable-length processing routes that span a large number of heterogeneous physical processes. To compute the attribution score of each process given a detected high defect density on a specific wafer, we propose a new algorithm that compares two counterfactual outcomes derived from partial process trajectories. This is enabled by new representation learning methods, proc2vec and route2vec. We demonstrate the effectiveness of the proposed framework using real wafer history data from the NY CREATES fab in Albany.

Path Learning with Trajectory Advantage Regression

In this paper, we propose trajectory advantage regression, a method of offline path learning and path attribution based on reinforcement learning. The proposed method can be used to solve path optimization problems while algorithmically only solving a regression problem.

A Provable Approach for End-to-End Safe Reinforcement Learning

A longstanding goal in safe reinforcement learning (RL) is a method to ensure the safety of a policy throughout the entire process, from learning to operation. However, existing safe RL paradigms inherently struggle to achieve this objective. We propose a method, called Provably Lifetime Safe RL (PLS), that integrates offline safe RL with safe policy deployment to address this challenge. Our proposed method learns a policy offline using return-conditioned supervised learning and then deploys the resulting policy while cautiously optimizing a limited set of parameters, known as target returns, using Gaussian processes (GPs). Theoretically, we justify the use of GPs by analyzing the mathematical relationship between target and actual returns. We then prove that PLS finds near-optimal target returns while guaranteeing safety with high probability. Empirically, we demonstrate that PLS outperforms baselines both in safety and reward performance, thereby achieving the longstanding goal to obtain high rewards while ensuring the safety of a policy throughout the lifetime from learning to operation.

Cumulative Stay-time Representation for Electronic Health Records in Medical Event Time Prediction

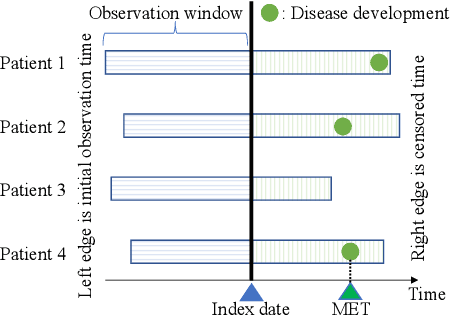
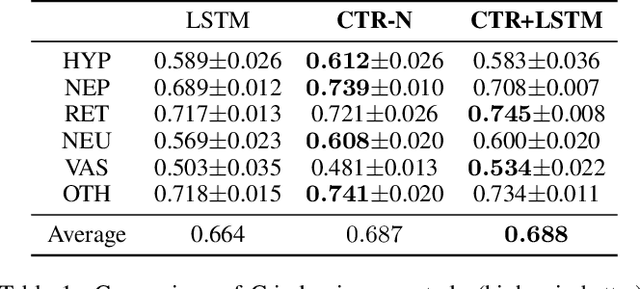
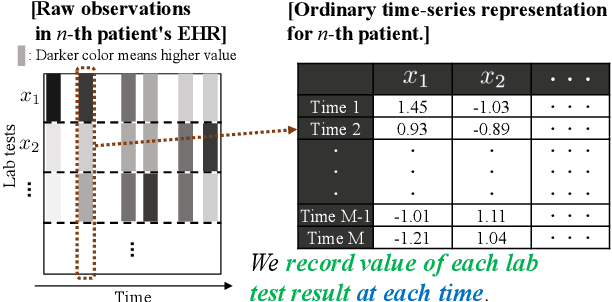
We address the problem of predicting when a disease will develop, i.e., medical event time (MET), from a patient's electronic health record (EHR). The MET of non-communicable diseases like diabetes is highly correlated to cumulative health conditions, more specifically, how much time the patient spent with specific health conditions in the past. The common time-series representation is indirect in extracting such information from EHR because it focuses on detailed dependencies between values in successive observations, not cumulative information. We propose a novel data representation for EHR called cumulative stay-time representation (CTR), which directly models such cumulative health conditions. We derive a trainable construction of CTR based on neural networks that has the flexibility to fit the target data and scalability to handle high-dimensional EHR. Numerical experiments using synthetic and real-world datasets demonstrate that CTR alone achieves a high prediction performance, and it enhances the performance of existing models when combined with them.

Biases in In Silico Evaluation of Molecular Optimization Methods and Bias-Reduced Evaluation Methodology

We are interested in in silico evaluation methodology for molecular optimization methods. Given a sample of molecules and their properties of our interest, we wish not only to train an agent that can find molecules optimized with respect to the target property but also to evaluate its performance. A common practice is to train a predictor of the target property on the sample and use it for both training and evaluating the agent. We show that this evaluator potentially suffers from two biases; one is due to misspecification of the predictor and the other to reusing the same sample for training and evaluation. We discuss bias reduction methods for each of the biases comprehensively, and empirically investigate their effectiveness.

A Theoretical Framework of Almost Hyperparameter-free Hyperparameter Selection Methods for Offline Policy Evaluation

We are concerned with the problem of hyperparameter selection of offline policy evaluation (OPE). OPE is a key component of offline reinforcement learning, which is a core technology for data-driven decision optimization without environment simulators. However, the current state-of-the-art OPE methods are not hyperparameter-free, which undermines their utility in real-life applications. We address this issue by introducing a new approximate hyperparameter selection (AHS) framework for OPE, which defines a notion of optimality (called selection criteria) in a quantitative and interpretable manner without hyperparameters. We then derive four AHS methods each of which has different characteristics such as convergence rate and time complexity. Finally, we verify effectiveness and limitation of these methods with a preliminary experiment.

PAC-Bayesian Transportation Bound

We present a new generalization error bound, the \emph{PAC-Bayesian transportation bound}, unifying the PAC-Bayesian analysis and the generic chaining method in view of the optimal transportation. The proposed bound is the first PAC-Bayesian framework that characterizes the cost of de-randomization of stochastic predictors facing any Lipschitz loss functions. As an example, we give an upper bound on the de-randomization cost of spectrally normalized neural networks~(NNs) to evaluate how much randomness contributes to the generalization of NNs.

Adaptive Minimax Regret against Smooth Logarithmic Losses over High-Dimensional $\ell_1$-Balls via Envelope Complexity

We develop a new theoretical framework, the \emph{envelope complexity}, to analyze the minimax regret with logarithmic loss functions and derive a Bayesian predictor that adaptively achieves the minimax regret over high-dimensional $\ell_1$-balls within a factor of two. The prior is newly derived for achieving the minimax regret and called the \emph{spike-and-tails~(ST) prior} as it looks like. The resulting regret bound is so simple that it is completely determined with the smoothness of the loss function and the radius of the balls except with logarithmic factors, and it has a generalized form of existing regret/risk bounds. In the preliminary experiment, we confirm that the ST prior outperforms the conventional minimax-regret prior under non-high-dimensional asymptotics.

High-dimensional Penalty Selection via Minimum Description Length Principle

We tackle the problem of penalty selection of regularization on the basis of the minimum description length (MDL) principle. In particular, we consider that the design space of the penalty function is high-dimensional. In this situation, the luckiness-normalized-maximum-likelihood(LNML)-minimization approach is favorable, because LNML quantifies the goodness of regularized models with any forms of penalty functions in view of the minimum description length principle, and guides us to a good penalty function through the high-dimensional space. However, the minimization of LNML entails two major challenges: 1) the computation of the normalizing factor of LNML and 2) its minimization in high-dimensional spaces. In this paper, we present a novel regularization selection method (MDL-RS), in which a tight upper bound of LNML (uLNML) is minimized with local convergence guarantee. Our main contribution is the derivation of uLNML, which is a uniform-gap upper bound of LNML in an analytic expression. This solves the above challenges in an approximate manner because it allows us to accurately approximate LNML and then efficiently minimize it. The experimental results show that MDL-RS improves the generalization performance of regularized estimates specifically when the model has redundant parameters.