LOA: Logical Optimal Actions for Text-based Interaction Games

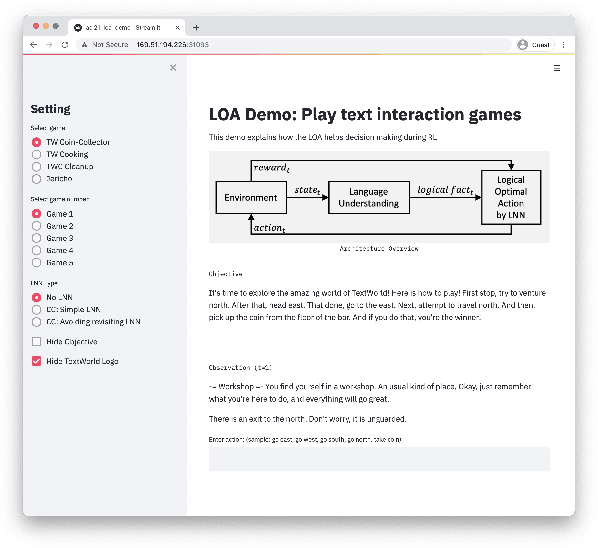
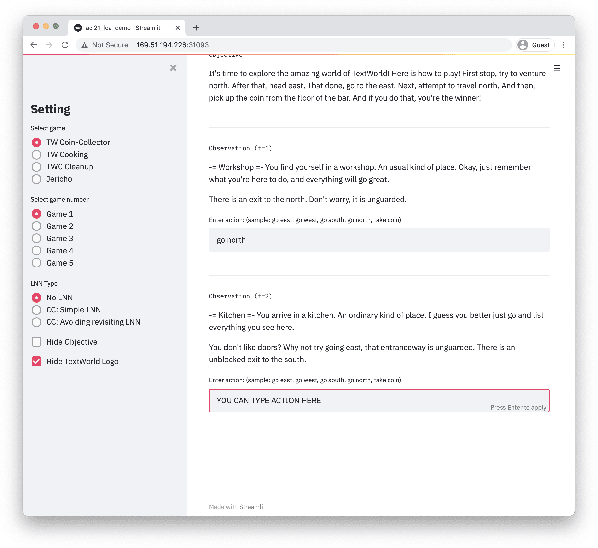
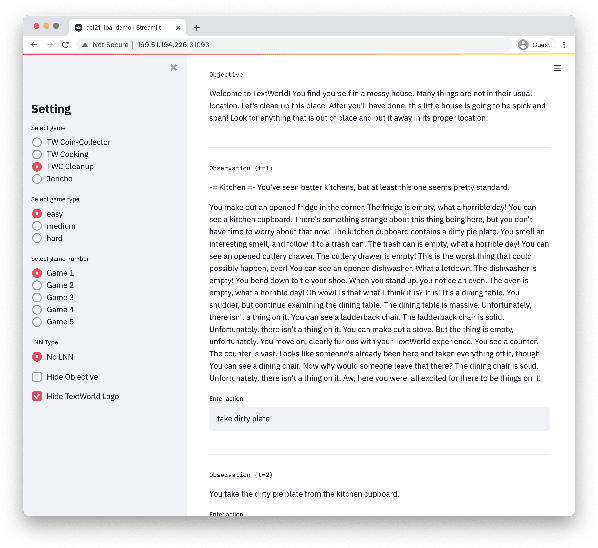
We present Logical Optimal Actions (LOA), an action decision architecture of reinforcement learning applications with a neuro-symbolic framework which is a combination of neural network and symbolic knowledge acquisition approach for natural language interaction games. The demonstration for LOA experiments consists of a web-based interactive platform for text-based games and visualization for acquired knowledge for improving interpretability for trained rules. This demonstration also provides a comparison module with other neuro-symbolic approaches as well as non-symbolic state-of-the-art agent models on the same text-based games. Our LOA also provides open-sourced implementation in Python for the reinforcement learning environment to facilitate an experiment for studying neuro-symbolic agents. Code: https://github.com/ibm/loa

Neuro-Symbolic Reinforcement Learning with First-Order Logic

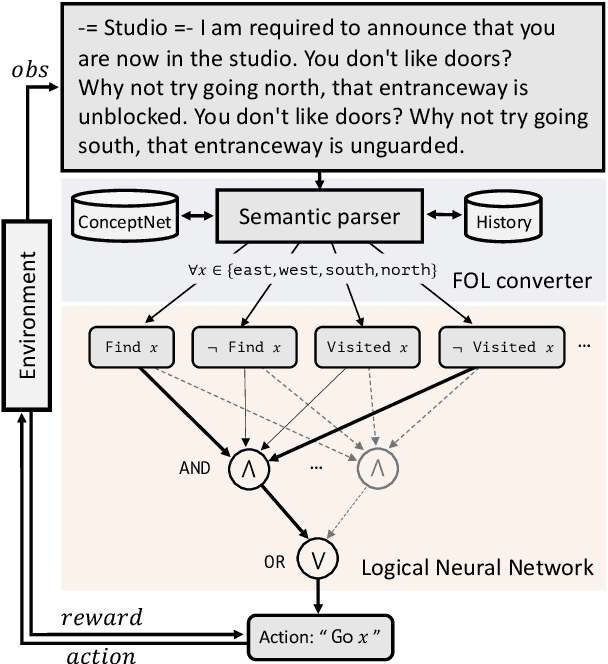
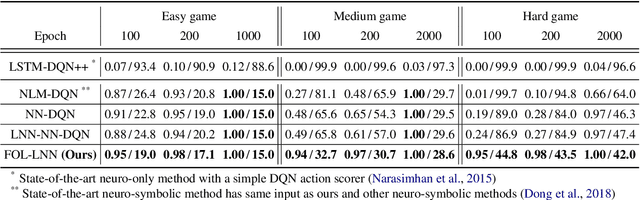
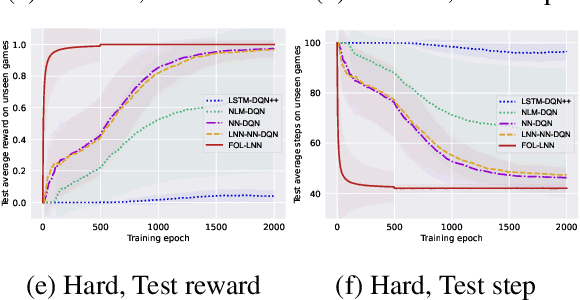
Deep reinforcement learning (RL) methods often require many trials before convergence, and no direct interpretability of trained policies is provided. In order to achieve fast convergence and interpretability for the policy in RL, we propose a novel RL method for text-based games with a recent neuro-symbolic framework called Logical Neural Network, which can learn symbolic and interpretable rules in their differentiable network. The method is first to extract first-order logical facts from text observation and external word meaning network (ConceptNet), then train a policy in the network with directly interpretable logical operators. Our experimental results show RL training with the proposed method converges significantly faster than other state-of-the-art neuro-symbolic methods in a TextWorld benchmark.

Time-Discounting Convolution for Event Sequences with Ambiguous Timestamps

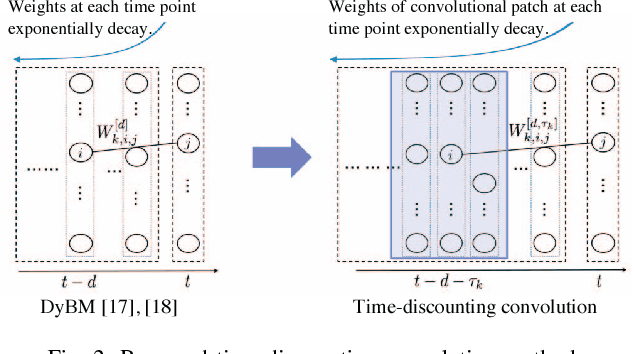
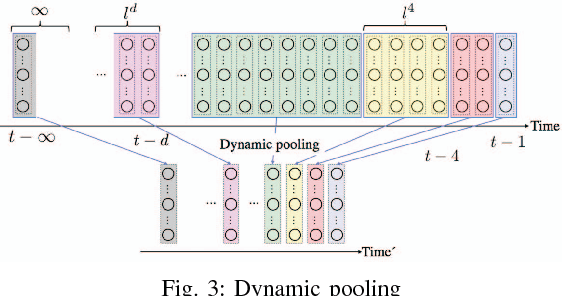
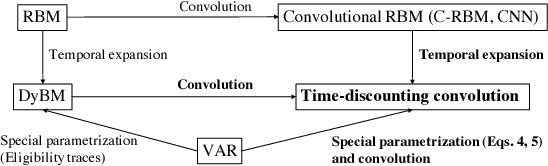
This paper proposes a method for modeling event sequences with ambiguous timestamps, a time-discounting convolution. Unlike in ordinary time series, time intervals are not constant, small time-shifts have no significant effect, and inputting timestamps or time durations into a model is not effective. The criteria that we require for the modeling are providing robustness against time-shifts or timestamps uncertainty as well as maintaining the essential capabilities of time-series models, i.e., forgetting meaningless past information and handling infinite sequences. The proposed method handles them with a convolutional mechanism across time with specific parameterizations, which efficiently represents the event dependencies in a time-shift invariant manner while discounting the effect of past events, and a dynamic pooling mechanism, which provides robustness against the uncertainty in timestamps and enhances the time-discounting capability by dynamically changing the pooling window size. In our learning algorithm, the decaying and dynamic pooling mechanisms play critical roles in handling infinite and variable length sequences. Numerical experiments on real-world event sequences with ambiguous timestamps and ordinary time series demonstrated the advantages of our method.