Proper Scoring Rules for Survival Analysis

Survival analysis is the problem of estimating probability distributions for future event times, which can be seen as a problem in uncertainty quantification. Although there are fundamental theories on strictly proper scoring rules for uncertainty quantification, little is known about those for survival analysis. In this paper, we investigate extensions of four major strictly proper scoring rules for survival analysis and we prove that these extensions are proper under certain conditions, which arise from the discretization of the estimation of probability distributions. We also compare the estimation performances of these extended scoring rules by using real datasets, and the extensions of the logarithmic score and the Brier score performed the best.

Sampler for Composition Ratio by Markov Chain Monte Carlo

Invention involves combination, or more precisely, ratios of composition. According to Thomas Edison, "Genius is one percent inspiration and 99 percent perspiration" is an example. In many situations, researchers and inventors already have a variety of data and manage to create something new by using it, but the key problem is how to select and combine knowledge. In this paper, we propose a new Markov chain Monte Carlo (MCMC) algorithm to generate composition ratios, nonnegative-integer-valued vectors with two properties: (i) the sum of the elements of each vector is constant, and (ii) only a small number of elements is nonzero. These constraints make it difficult for existing MCMC algorithms to sample composition ratios. The key points of our approach are (1) designing an appropriate target distribution by using a condition on the number of nonzero elements, and (2) changing values only between a certain pair of elements in each iteration. Through an experiment on creating a new cocktail, we show that the combination of the proposed method with supervised learning can solve a creative problem.

Consistent Nonparametric Different-Feature Selection via the Sparsest $k$-Subgraph Problem

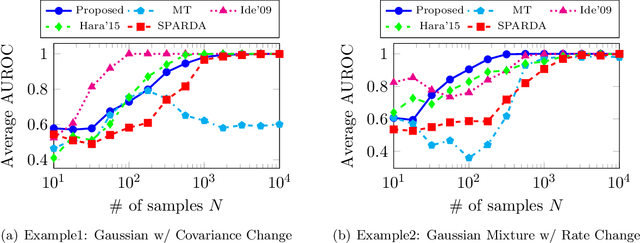
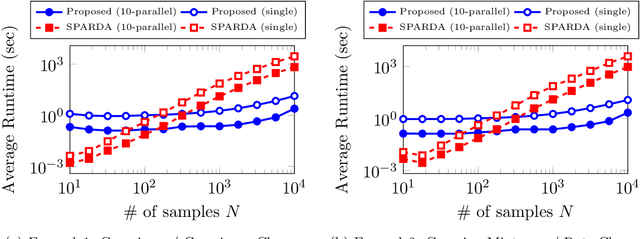
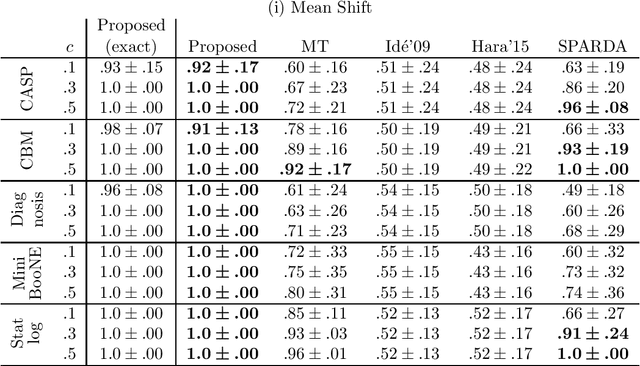
Two-sample feature selection is the problem of finding features that describe a difference between two probability distributions, which is a ubiquitous problem in both scientific and engineering studies. However, existing methods have limited applicability because of their restrictive assumptions on data distributoins or computational difficulty. In this paper, we resolve these difficulties by formulating the problem as a sparsest $k$-subgraph problem. The proposed method is nonparametric and does not assume any specific parametric models on the data distributions. We show that the proposed method is computationally efficient and does not require any extra computation for model selection. Moreover, we prove that the proposed method provides a consistent estimator of features under mild conditions. Our experimental results show that the proposed method outperforms the current method with regard to both accuracy and computation time.