Spacing Test for Fused Lasso

This study addresses the unresolved problem of selecting the regularization parameter in the fused lasso. In particular, we extend the framework of the Spacing Test proposed by Tibshirani et al. to the fused lasso, providing a theoretical foundation for post-selection inference by characterizing the selection event as a polyhedral constraint. Based on the analysis of the solution path of the fused lasso using a LARS-type algorithm, we derive exact conditional $p$-values for the selected change-points. Our method broadens the applicability of the Spacing Test from the standard lasso to fused penalty structures. Furthermore, through numerical experiments comparing the proposed method with sequential versions of AIC and BIC as well as cross-validation, we demonstrate that the proposed approach properly controls the type I error while achieving high detection power. This work offers a theoretically sound and computationally practical solution for parameter selection and post-selection inference in structured signal estimation problems. Keywords: Fused Lasso, Regularization parameter selection, Spacing Test for Lasso, Selective inference, Change-point detection

An Efficient Procedure for Computing Bayesian Network Structure Learning

We propose a globally optimal Bayesian network structure discovery algorithm based on a progressively leveled scoring approach. Bayesian network structure discovery is a fundamental yet NP-hard problem in the field of probabilistic graphical models, and as the number of variables increases, memory usage grows exponentially. The simple and effective method proposed by Silander and Myllym\"aki has been widely applied in this field, as it incrementally calculates local scores to achieve global optimality. However, existing methods that utilize disk storage, while capable of handling networks with a larger number of variables, introduce issues such as latency, fragmentation, and additional overhead associated with disk I/O operations. To avoid these problems, we explore how to further enhance computational efficiency and reduce peak memory usage using only memory. We introduce an efficient hierarchical computation method that requires only a single traversal of all local structures, retaining only the data and information necessary for the current computation, thereby improving efficiency and significantly reducing memory requirements. Experimental results indicate that our method, when using only memory, not only reduces peak memory usage but also improves computational efficiency compared to existing methods, demonstrating good scalability for handling larger networks and exhibiting stable experimental results. Ultimately, we successfully achieved the processing of a Bayesian network with 28 variables using only memory.

Learning under Singularity: An Information Criterion improving WBIC and sBIC

We introduce a novel Information Criterion (IC), termed Learning under Singularity (LS), designed to enhance the functionality of the Widely Applicable Bayes Information Criterion (WBIC) and the Singular Bayesian Information Criterion (sBIC). LS is effective without regularity constraints and demonstrates stability. Watanabe defined a statistical model or a learning machine as regular if the mapping from a parameter to a probability distribution is one-to-one and its Fisher information matrix is positive definite. In contrast, models not meeting these conditions are termed singular. Over the past decade, several information criteria for singular cases have been proposed, including WBIC and sBIC. WBIC is applicable in non-regular scenarios but faces challenges with large sample sizes and redundant estimation of known learning coefficients. Conversely, sBIC is limited in its broader application due to its dependence on maximum likelihood estimates. LS addresses these limitations by enhancing the utility of both WBIC and sBIC. It incorporates the empirical loss from the Widely Applicable Information Criterion (WAIC) to represent the goodness of fit to the statistical model, along with a penalty term similar to that of sBIC. This approach offers a flexible and robust method for model selection, free from regularity constraints.

Generalization of LiNGAM that allows confounding

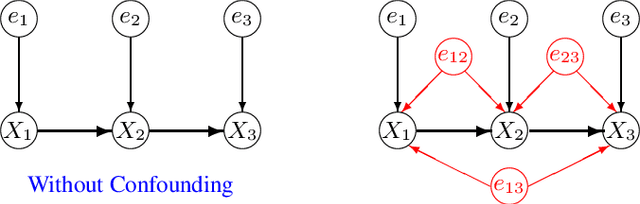
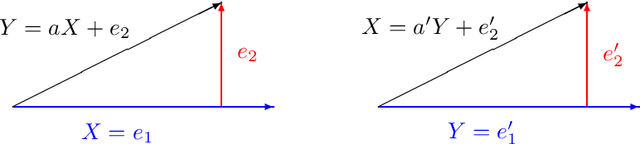
LiNGAM determines the variable order from cause to effect using additive noise models, but it faces challenges with confounding. Previous methods maintained LiNGAM's fundamental structure while trying to identify and address variables affected by confounding. As a result, these methods required significant computational resources regardless of the presence of confounding, and they did not ensure the detection of all confounding types. In contrast, this paper enhances LiNGAM by introducing LiNGAM-MMI, a method that quantifies the magnitude of confounding using KL divergence and arranges the variables to minimize its impact. This method efficiently achieves a globally optimal variable order through the shortest path problem formulation. LiNGAM-MMI processes data as efficiently as traditional LiNGAM in scenarios without confounding while effectively addressing confounding situations. Our experimental results suggest that LiNGAM-MMI more accurately determines the correct variable order, both in the presence and absence of confounding.

Functional Linear Non-Gaussian Acyclic Model for Causal Discovery

In causal discovery, non-Gaussianity has been used to characterize the complete configuration of a Linear Non-Gaussian Acyclic Model (LiNGAM), encompassing both the causal ordering of variables and their respective connection strengths. However, LiNGAM can only deal with the finite-dimensional case. To expand this concept, we extend the notion of variables to encompass vectors and even functions, leading to the Functional Linear Non-Gaussian Acyclic Model (Func-LiNGAM). Our motivation stems from the desire to identify causal relationships in brain-effective connectivity tasks involving, for example, fMRI and EEG datasets. We demonstrate why the original LiNGAM fails to handle these inherently infinite-dimensional datasets and explain the availability of functional data analysis from both empirical and theoretical perspectives. {We establish theoretical guarantees of the identifiability of the causal relationship among non-Gaussian random vectors and even random functions in infinite-dimensional Hilbert spaces.} To address the issue of sparsity in discrete time points within intrinsic infinite-dimensional functional data, we propose optimizing the coordinates of the vectors using functional principal component analysis. Experimental results on synthetic data verify the ability of the proposed framework to identify causal relationships among multivariate functions using the observed samples. For real data, we focus on analyzing the brain connectivity patterns derived from fMRI data.

Dropout Drops Double Descent

In this paper, we find and analyze that we can easily drop the double descent by only adding one dropout layer before the fully-connected linear layer. The surprising double-descent phenomenon has drawn public attention in recent years, making the prediction error rise and drop as we increase either sample or model size. The current paper shows that it is possible to alleviate these phenomena by using optimal dropout in the linear regression model and the nonlinear random feature regression, both theoretically and empirically. % ${y}=X{\beta}^0+{\epsilon}$ with $X\in\mathbb{R}^{n\times p}$. We obtain the optimal dropout hyperparameter by estimating the ground truth ${\beta}^0$ with generalized ridge typed estimator $\hat{{\beta}}=(X^TX+\alpha\cdot\mathrm{diag}(X^TX))^{-1}X^T{y}$. Moreover, we empirically show that optimal dropout can achieve a monotonic test error curve in nonlinear neural networks using Fashion-MNIST and CIFAR-10. Our results suggest considering dropout for risk curve scaling when meeting the peak phenomenon. In addition, we figure out why previous deep learning models do not encounter double-descent scenarios -- because we already apply a usual regularization approach like the dropout in our models. To our best knowledge, this paper is the first to analyze the relationship between dropout and double descent.

Causal Order Identification to Address Confounding: Binary Variables

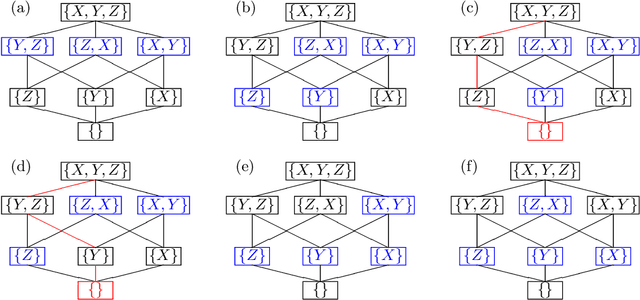
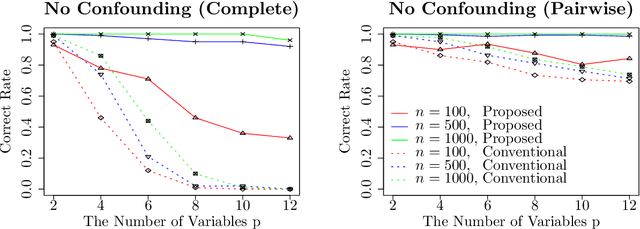
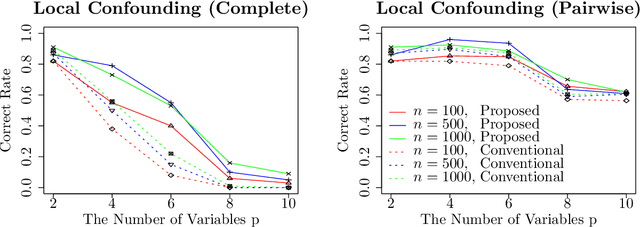
This paper considers an extension of the linear non-Gaussian acyclic model (LiNGAM) that determines the causal order among variables from a dataset when the variables are expressed by a set of linear equations, including noise. In particular, we assume that the variables are binary. The existing LiNGAM assumes that no confounding is present, which is restrictive in practice. Based on the concept of independent component analysis (ICA), this paper proposes an extended framework in which the mutual information among the noises is minimized. Another significant contribution is to reduce the realization of the shortest path problem. The distance between each pair of nodes expresses an associated mutual information value, and the path with the minimum sum (KL divergence) is sought. Although $p!$ mutual information values should be compared, this paper dramatically reduces the computation when no confounding is present. The proposed algorithm finds the globally optimal solution, while the existing locally greedily seek the order based on hypothesis testing. We use the best estimator in the sense of Bayes/MDL that correctly detects independence for mutual information estimation. Experiments using artificial and actual data show that the proposed version of LiNGAM achieves significantly better performance, particularly when confounding is present.

Efficient proximal gradient algorithms for joint graphical lasso

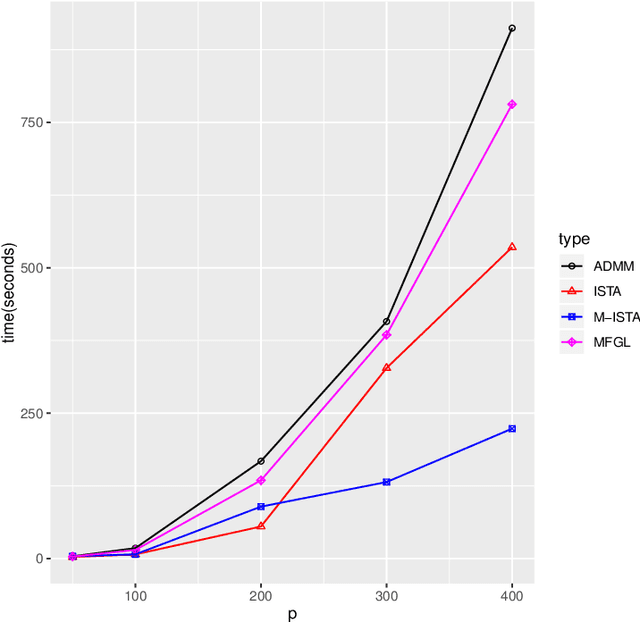
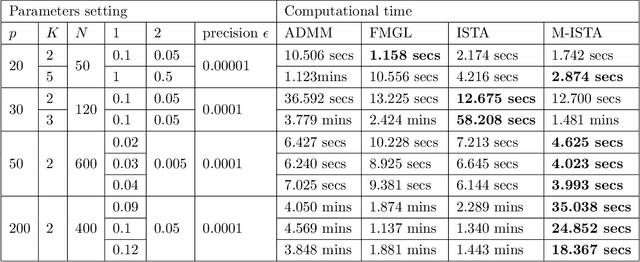
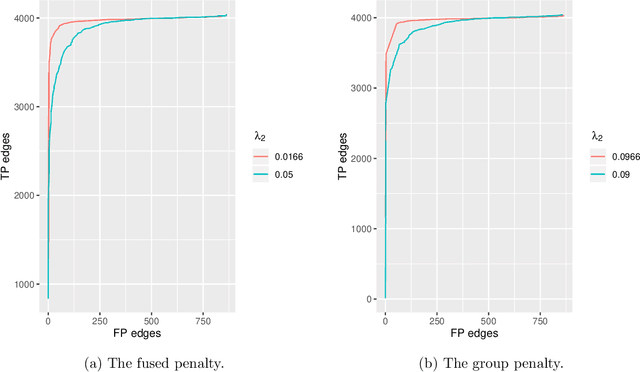
We consider learning an undirected graphical model from sparse data. While several efficient algorithms have been proposed for graphical lasso (GL), the alternating direction method of multipliers (ADMM) is the main approach taken concerning for joint graphical lasso (JGL). We propose proximal gradient procedures with and without a backtracking option for the JGL. These procedures are first-order and relatively simple, and the subproblems are solved efficiently in closed form. We further show the boundedness for the solution of the JGL problem and the iterations in the algorithms. The numerical results indicate that the proposed algorithms can achieve high accuracy and precision, and their efficiency is competitive with state-of-the-art algorithms.

Converting ADMM to a Proximal Gradient for Convex Optimization Problems

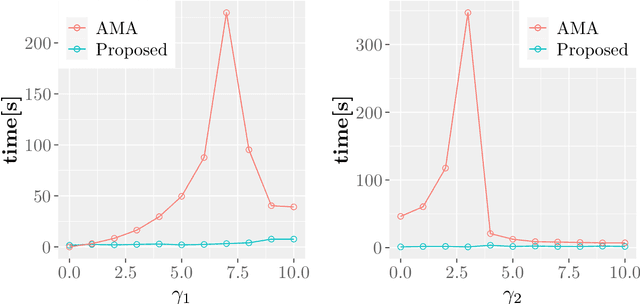
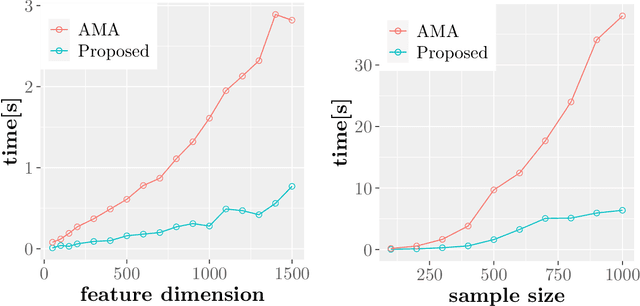
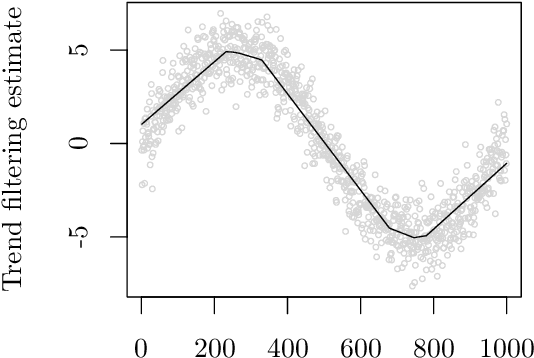
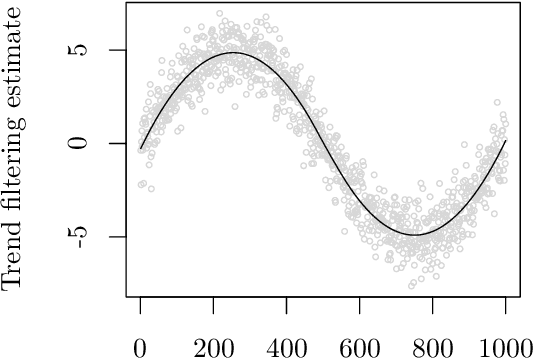
In machine learning and data science, we often consider efficiency for solving problems. In sparse estimation, such as fused lasso and convex clustering, we apply either the proximal gradient method or the alternating direction method of multipliers (ADMM) to solve the problem. It takes time to include matrix division in the former case, while an efficient method such as FISTA (fast iterative shrinkage-thresholding algorithm) has been developed in the latter case. This paper proposes a general method for converting the ADMM solution to the proximal gradient method, assuming that the constraints and objectives are strongly convex. Then, we apply it to sparse estimation problems, such as sparse convex clustering and trend filtering, and we show by numerical experiments that we can obtain a significant improvement in terms of efficiency.

A Theoretical Analysis of the BDeu Scores in Bayesian Network Structure Learning

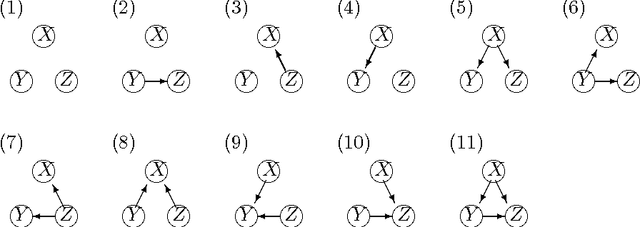
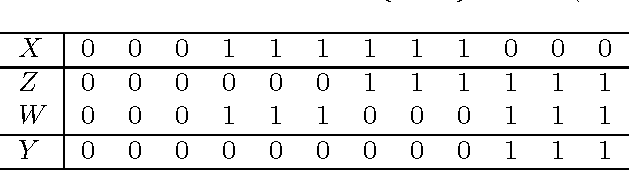
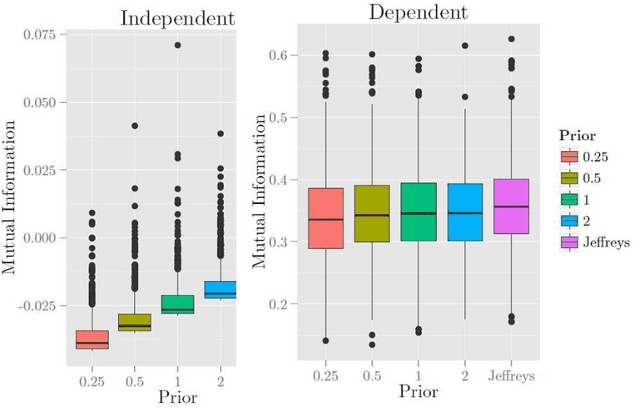
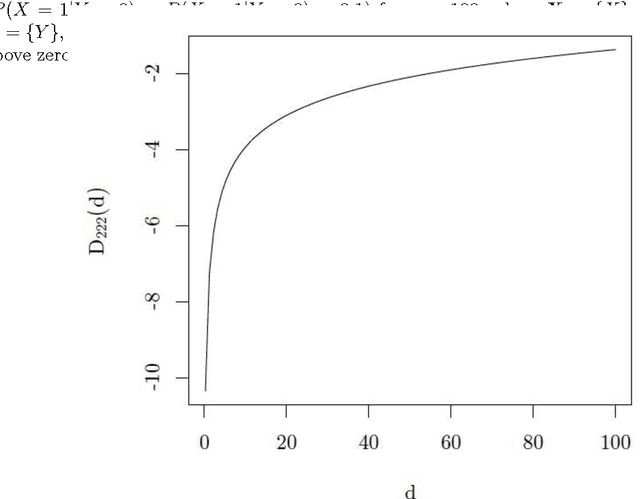
In Bayesian network structure learning (BNSL), we need the prior probability over structures and parameters. If the former is the uniform distribution, the latter determines the correctness of BNSL. In this paper, we compare BDeu (Bayesian Dirichlet equivalent uniform) and Jeffreys' prior w.r.t. their consistency. When we seek a parent set $U$ of a variable $X$, we require regularity that if $H(X|U)\leq H(X|U')$ and $U\subsetneq U'$, then $U$ should be chosen rather than $U'$. We prove that the BDeu scores violate the property and cause fatal situations in BNSL. This is because for the BDeu scores, for any sample size $n$,there exists a probability in the form $P(X,Y,Z)={P(XZ)P(YZ)}/{P(Z)}$ such that the probability of deciding that $X$ and $Y$ are not conditionally independent given $Z$ is more than a half. For Jeffreys' prior, the false-positive probability uniformly converges to zero without depending on any parameter values, and no such an inconvenience occurs.