A Theoretical Analysis of the BDeu Scores in Bayesian Network Structure Learning
Paper and Code
Dec 02, 2016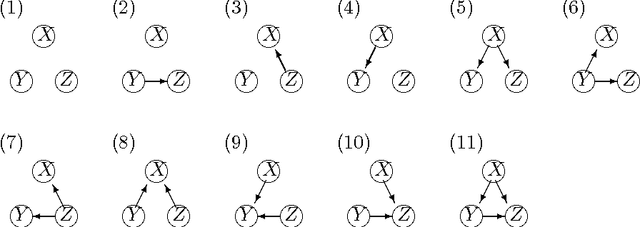
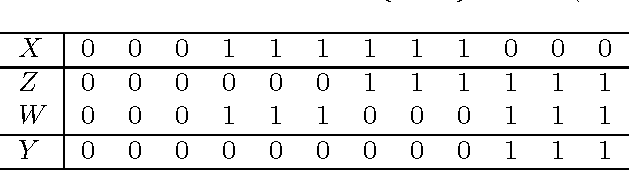
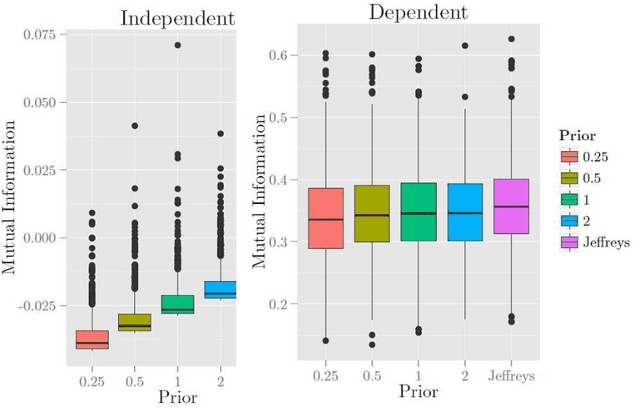
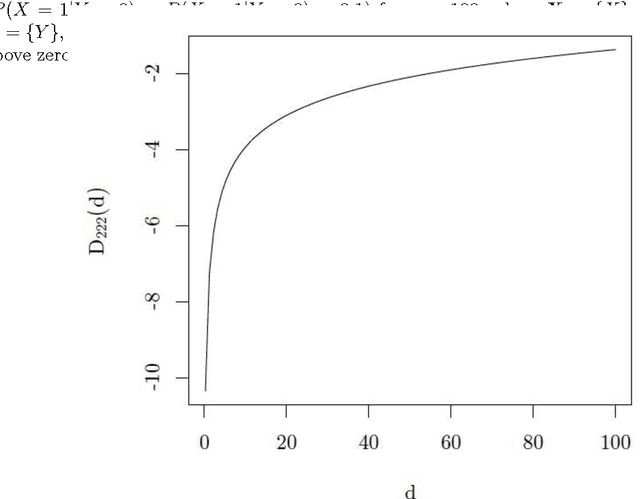
In Bayesian network structure learning (BNSL), we need the prior probability over structures and parameters. If the former is the uniform distribution, the latter determines the correctness of BNSL. In this paper, we compare BDeu (Bayesian Dirichlet equivalent uniform) and Jeffreys' prior w.r.t. their consistency. When we seek a parent set $U$ of a variable $X$, we require regularity that if $H(X|U)\leq H(X|U')$ and $U\subsetneq U'$, then $U$ should be chosen rather than $U'$. We prove that the BDeu scores violate the property and cause fatal situations in BNSL. This is because for the BDeu scores, for any sample size $n$,there exists a probability in the form $P(X,Y,Z)={P(XZ)P(YZ)}/{P(Z)}$ such that the probability of deciding that $X$ and $Y$ are not conditionally independent given $Z$ is more than a half. For Jeffreys' prior, the false-positive probability uniformly converges to zero without depending on any parameter values, and no such an inconvenience occurs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge