Converting ADMM to a Proximal Gradient for Convex Optimization Problems
Paper and Code
Apr 22, 2021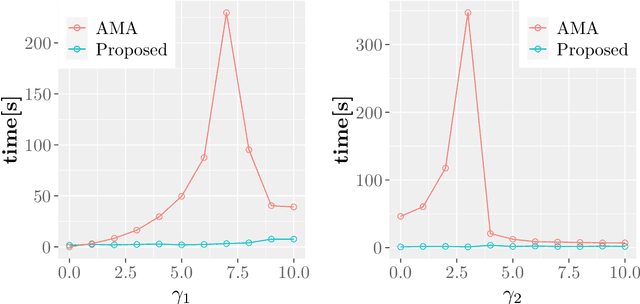
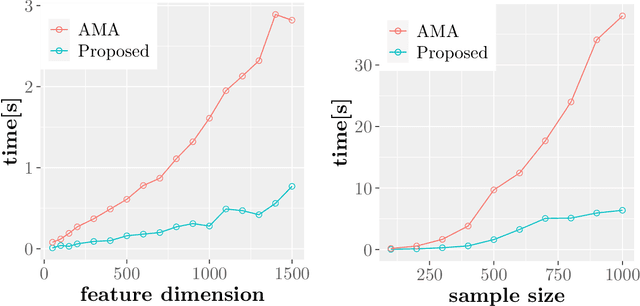
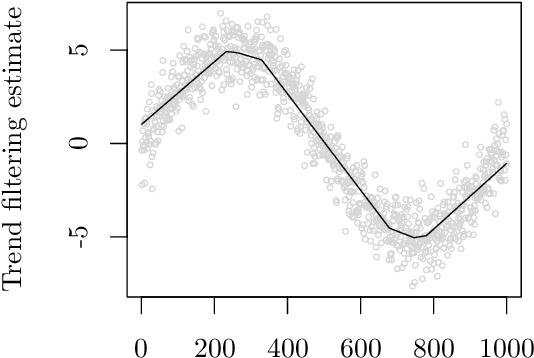
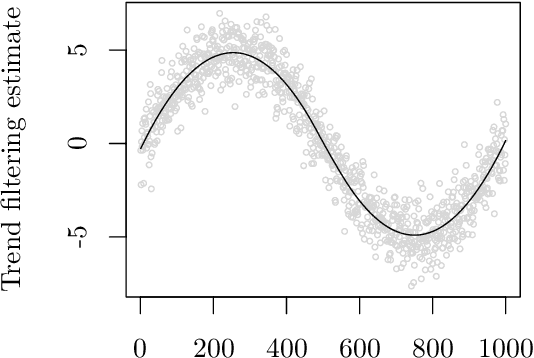
In machine learning and data science, we often consider efficiency for solving problems. In sparse estimation, such as fused lasso and convex clustering, we apply either the proximal gradient method or the alternating direction method of multipliers (ADMM) to solve the problem. It takes time to include matrix division in the former case, while an efficient method such as FISTA (fast iterative shrinkage-thresholding algorithm) has been developed in the latter case. This paper proposes a general method for converting the ADMM solution to the proximal gradient method, assuming that the constraints and objectives are strongly convex. Then, we apply it to sparse estimation problems, such as sparse convex clustering and trend filtering, and we show by numerical experiments that we can obtain a significant improvement in terms of efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge