Efficient proximal gradient algorithms for joint graphical lasso

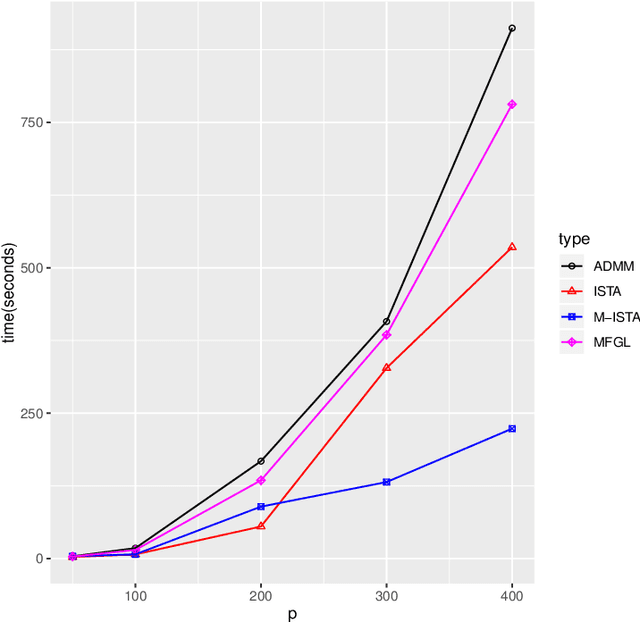
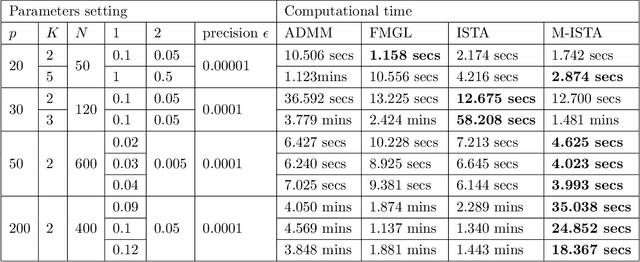
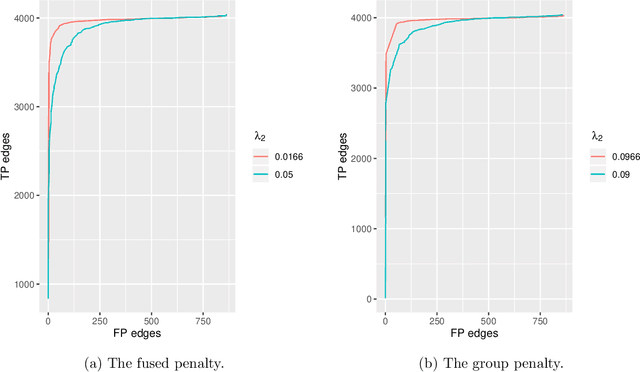
We consider learning an undirected graphical model from sparse data. While several efficient algorithms have been proposed for graphical lasso (GL), the alternating direction method of multipliers (ADMM) is the main approach taken concerning for joint graphical lasso (JGL). We propose proximal gradient procedures with and without a backtracking option for the JGL. These procedures are first-order and relatively simple, and the subproblems are solved efficiently in closed form. We further show the boundedness for the solution of the JGL problem and the iterations in the algorithms. The numerical results indicate that the proposed algorithms can achieve high accuracy and precision, and their efficiency is competitive with state-of-the-art algorithms.

Converting ADMM to a Proximal Gradient for Convex Optimization Problems

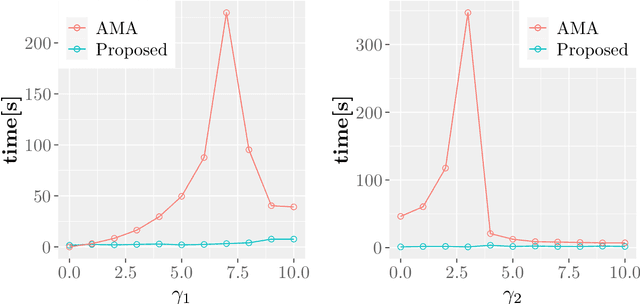
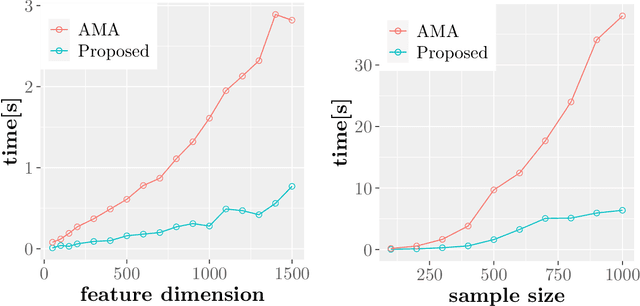
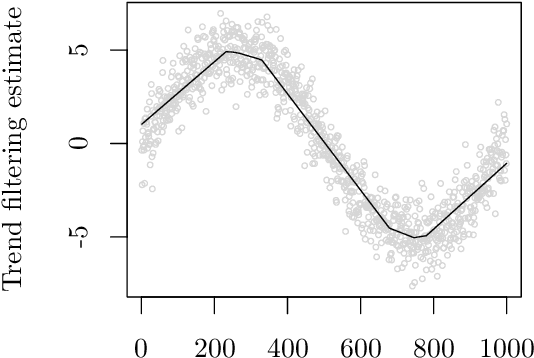
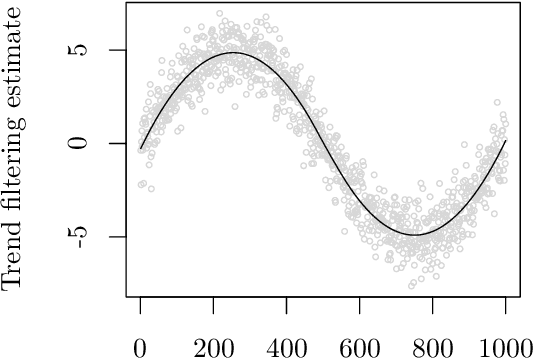
In machine learning and data science, we often consider efficiency for solving problems. In sparse estimation, such as fused lasso and convex clustering, we apply either the proximal gradient method or the alternating direction method of multipliers (ADMM) to solve the problem. It takes time to include matrix division in the former case, while an efficient method such as FISTA (fast iterative shrinkage-thresholding algorithm) has been developed in the latter case. This paper proposes a general method for converting the ADMM solution to the proximal gradient method, assuming that the constraints and objectives are strongly convex. Then, we apply it to sparse estimation problems, such as sparse convex clustering and trend filtering, and we show by numerical experiments that we can obtain a significant improvement in terms of efficiency.