Generalization of LiNGAM that allows confounding

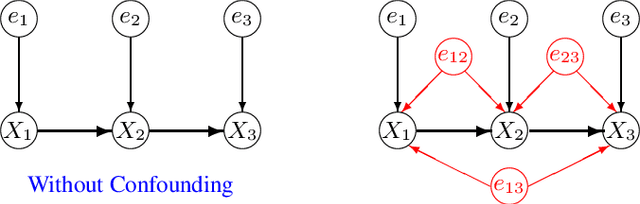
LiNGAM determines the variable order from cause to effect using additive noise models, but it faces challenges with confounding. Previous methods maintained LiNGAM's fundamental structure while trying to identify and address variables affected by confounding. As a result, these methods required significant computational resources regardless of the presence of confounding, and they did not ensure the detection of all confounding types. In contrast, this paper enhances LiNGAM by introducing LiNGAM-MMI, a method that quantifies the magnitude of confounding using KL divergence and arranges the variables to minimize its impact. This method efficiently achieves a globally optimal variable order through the shortest path problem formulation. LiNGAM-MMI processes data as efficiently as traditional LiNGAM in scenarios without confounding while effectively addressing confounding situations. Our experimental results suggest that LiNGAM-MMI more accurately determines the correct variable order, both in the presence and absence of confounding.

Functional Linear Non-Gaussian Acyclic Model for Causal Discovery

In causal discovery, non-Gaussianity has been used to characterize the complete configuration of a Linear Non-Gaussian Acyclic Model (LiNGAM), encompassing both the causal ordering of variables and their respective connection strengths. However, LiNGAM can only deal with the finite-dimensional case. To expand this concept, we extend the notion of variables to encompass vectors and even functions, leading to the Functional Linear Non-Gaussian Acyclic Model (Func-LiNGAM). Our motivation stems from the desire to identify causal relationships in brain-effective connectivity tasks involving, for example, fMRI and EEG datasets. We demonstrate why the original LiNGAM fails to handle these inherently infinite-dimensional datasets and explain the availability of functional data analysis from both empirical and theoretical perspectives. {We establish theoretical guarantees of the identifiability of the causal relationship among non-Gaussian random vectors and even random functions in infinite-dimensional Hilbert spaces.} To address the issue of sparsity in discrete time points within intrinsic infinite-dimensional functional data, we propose optimizing the coordinates of the vectors using functional principal component analysis. Experimental results on synthetic data verify the ability of the proposed framework to identify causal relationships among multivariate functions using the observed samples. For real data, we focus on analyzing the brain connectivity patterns derived from fMRI data.

Dropout Drops Double Descent

In this paper, we find and analyze that we can easily drop the double descent by only adding one dropout layer before the fully-connected linear layer. The surprising double-descent phenomenon has drawn public attention in recent years, making the prediction error rise and drop as we increase either sample or model size. The current paper shows that it is possible to alleviate these phenomena by using optimal dropout in the linear regression model and the nonlinear random feature regression, both theoretically and empirically. % ${y}=X{\beta}^0+{\epsilon}$ with $X\in\mathbb{R}^{n\times p}$. We obtain the optimal dropout hyperparameter by estimating the ground truth ${\beta}^0$ with generalized ridge typed estimator $\hat{{\beta}}=(X^TX+\alpha\cdot\mathrm{diag}(X^TX))^{-1}X^T{y}$. Moreover, we empirically show that optimal dropout can achieve a monotonic test error curve in nonlinear neural networks using Fashion-MNIST and CIFAR-10. Our results suggest considering dropout for risk curve scaling when meeting the peak phenomenon. In addition, we figure out why previous deep learning models do not encounter double-descent scenarios -- because we already apply a usual regularization approach like the dropout in our models. To our best knowledge, this paper is the first to analyze the relationship between dropout and double descent.