Breaking the curse of dimensionality with Isolation Kernel
Paper and Code
Sep 29, 2021
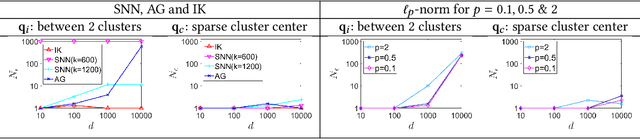
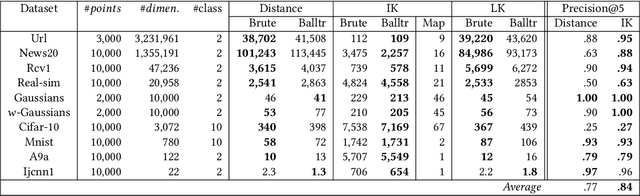
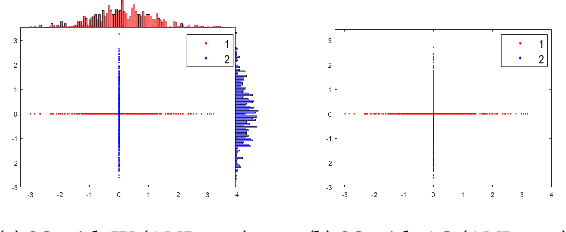
The curse of dimensionality has been studied in different aspects. However, breaking the curse has been elusive. We show for the first time that it is possible to break the curse using the recently introduced Isolation Kernel. We show that only Isolation Kernel performs consistently well in indexed search, spectral & density peaks clustering, SVM classification and t-SNE visualization in both low and high dimensions, compared with distance, Gaussian and linear kernels. This is also supported by our theoretical analyses that Isolation Kernel is the only kernel that has the provable ability to break the curse, compared with existing metric-based Lipschitz continuous kernels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge