Dual Riemannian Newton Method on Statistical Manifolds

In probabilistic modeling, parameter estimation is commonly formulated as a minimization problem on a parameter manifold. Optimization in such spaces requires geometry-aware methods that respect the underlying information structure. While the natural gradient leverages the Fisher information metric as a form of Riemannian gradient descent, it remains a first-order method and often exhibits slow convergence near optimal solutions. Existing second-order manifold algorithms typically rely on the Levi-Civita connection, thus overlooking the dual-connection structure that is central to information geometry. We propose the dual Riemannian Newton method, a Newton-type optimization algorithm on manifolds endowed with a metric and a pair of dual affine connections. The dual Riemannian Newton method explicates how duality shapes second-order updates: when the retraction (a local surrogate of the exponential map) is defined by one connection, the associated Newton equation is posed with its dual. We establish local quadratic convergence and validate the theory with experiments on representative statistical models. Thus, the dual Riemannian Newton method thus delivers second-order efficiency while remaining compatible with the dual structures that underlie modern information-geometric learning and inference.

New Evidence of the Two-Phase Learning Dynamics of Neural Networks

Understanding how deep neural networks learn remains a fundamental challenge in modern machine learning. A growing body of evidence suggests that training dynamics undergo a distinct phase transition, yet our understanding of this transition is still incomplete. In this paper, we introduce an interval-wise perspective that compares network states across a time window, revealing two new phenomena that illuminate the two-phase nature of deep learning. i) \textbf{The Chaos Effect.} By injecting an imperceptibly small parameter perturbation at various stages, we show that the response of the network to the perturbation exhibits a transition from chaotic to stable, suggesting there is an early critical period where the network is highly sensitive to initial conditions; ii) \textbf{The Cone Effect.} Tracking the evolution of the empirical Neural Tangent Kernel (eNTK), we find that after this transition point the model's functional trajectory is confined to a narrow cone-shaped subset: while the kernel continues to change, it gets trapped into a tight angular region. Together, these effects provide a structural, dynamical view of how deep networks transition from sensitive exploration to stable refinement during training.

Bringing Structure to Naturalness: On the Naturalness of ASTs

Source code comes in different shapes and forms. Previous research has already shown code to be more predictable than natural language as well as highlighted its statistical predictability at the token level: source code can be natural. More recently, the structure of code -- control flow, syntax graphs, abstract syntax trees etc. -- has been successfully used to improve the state-of-the-art on numerous tasks: code suggestion, code summarisation, method naming etc. This body of work implicitly assumes that structured representations of code are similarly statistically predictable, i.e. that a structured view of code is also natural. We consider that this view should be made explicit and propose directly studying the Structured Naturalness Hypothesis. Beyond just naming existing research that assumes this hypothesis and formulating it, we also provide evidence in the case of trees: TreeLSTM models over ASTs for some languages, such as Ruby, are competitive with $n$-gram models while handling the syntax token issue highlighted by previous research 'for free'. For other languages, such as Java or Python, we find tree models to perform worse, suggesting that downstream task improvement is uncorrelated to the language modelling task. Further, we show how such naturalness signals can be employed for near state-of-the-art results on just-in-time defect prediction while forgoing manual feature engineering work.

On the Cone Effect in the Learning Dynamics

Understanding the learning dynamics of neural networks is a central topic in the deep learning community. In this paper, we take an empirical perspective to study the learning dynamics of neural networks in real-world settings. Specifically, we investigate the evolution process of the empirical Neural Tangent Kernel (eNTK) during training. Our key findings reveal a two-phase learning process: i) in Phase I, the eNTK evolves significantly, signaling the rich regime, and ii) in Phase II, the eNTK keeps evolving but is constrained in a narrow space, a phenomenon we term the cone effect. This two-phase framework builds on the hypothesis proposed by Fort et al. (2020), but we uniquely identify the cone effect in Phase II, demonstrating its significant performance advantages over fully linearized training.

A Complete Decomposition of KL Error using Refined Information and Mode Interaction Selection

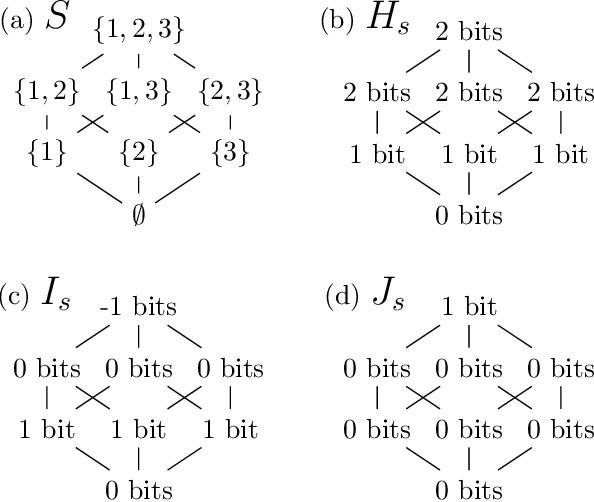
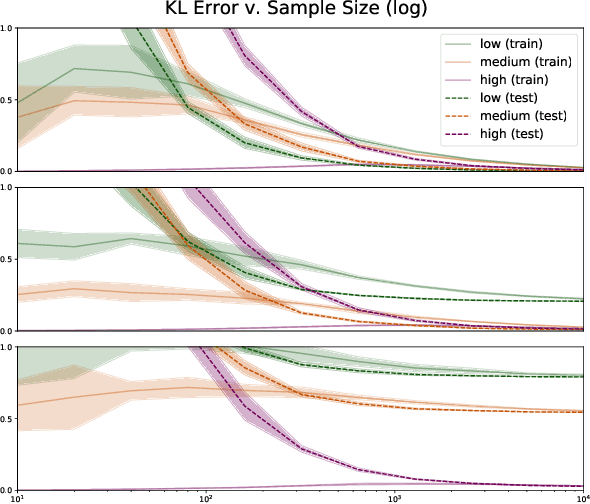
The log-linear model has received a significant amount of theoretical attention in previous decades and remains the fundamental tool used for learning probability distributions over discrete variables. Despite its large popularity in statistical mechanics and high-dimensional statistics, the vast majority of such energy-based modeling approaches only focus on the two-variable relationships, such as Boltzmann machines and Markov graphical models. Although these approaches have easier-to-solve structure learning problems and easier-to-optimize parametric distributions, they often ignore the rich structure which exists in the higher-order interactions between different variables. Using more recent tools from the field of information geometry, we revisit the classical formulation of the log-linear model with a focus on higher-order mode interactions, going beyond the 1-body modes of independent distributions and the 2-body modes of Boltzmann distributions. This perspective allows us to define a complete decomposition of the KL error. This then motivates the formulation of a sparse selection problem over the set of possible mode interactions. In the same way as sparse graph selection allows for better generalization, we find that our learned distributions are able to more efficiently use the finite amount of data which is available in practice. On both synthetic and real-world datasets, we demonstrate our algorithm's effectiveness in maximizing the log-likelihood for the generative task and also the ease of adaptability to the discriminative task of classification.

Pseudo-Non-Linear Data Augmentation via Energy Minimization

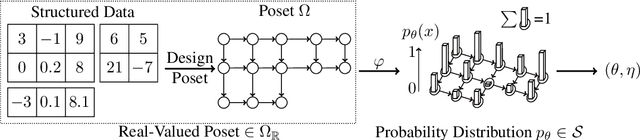
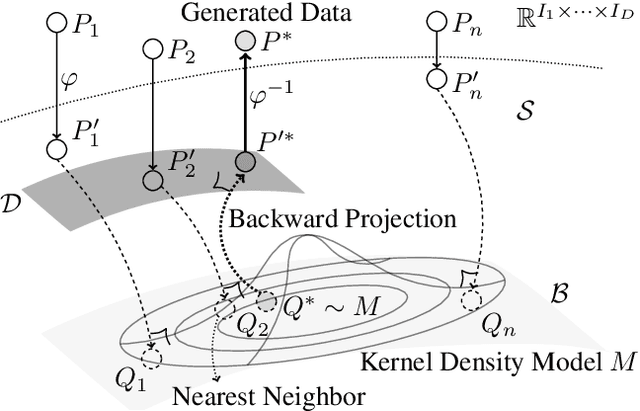
We propose a novel and interpretable data augmentation method based on energy-based modeling and principles from information geometry. Unlike black-box generative models, which rely on deep neural networks, our approach replaces these non-interpretable transformations with explicit, theoretically grounded ones, ensuring interpretability and strong guarantees such as energy minimization. Central to our method is the introduction of the backward projection algorithm, which reverses dimension reduction to generate new data. Empirical results demonstrate that our method achieves competitive performance with black-box generative models while offering greater transparency and interpretability.

Linear Mode Connectivity in Differentiable Tree Ensembles

Linear Mode Connectivity (LMC) refers to the phenomenon that performance remains consistent for linearly interpolated models in the parameter space. For independently optimized model pairs from different random initializations, achieving LMC is considered crucial for validating the stable success of the non-convex optimization in modern machine learning models and for facilitating practical parameter-based operations such as model merging. While LMC has been achieved for neural networks by considering the permutation invariance of neurons in each hidden layer, its attainment for other models remains an open question. In this paper, we first achieve LMC for soft tree ensembles, which are tree-based differentiable models extensively used in practice. We show the necessity of incorporating two invariances: subtree flip invariance and splitting order invariance, which do not exist in neural networks but are inherent to tree architectures, in addition to permutation invariance of trees. Moreover, we demonstrate that it is even possible to exclude such additional invariances while keeping LMC by designing decision list-based tree architectures, where such invariances do not exist by definition. Our findings indicate the significance of accounting for architecture-specific invariances in achieving LMC.

StiefelGen: A Simple, Model Agnostic Approach for Time Series Data Augmentation over Riemannian Manifolds

Data augmentation is an area of research which has seen active development in many machine learning fields, such as in image-based learning models, reinforcement learning for self driving vehicles, and general noise injection for point cloud data. However, convincing methods for general time series data augmentation still leaves much to be desired, especially since the methods developed for these models do not readily cross-over. Three common approaches for time series data augmentation include: (i) Constructing a physics-based model and then imbuing uncertainty over the coefficient space (for example), (ii) Adding noise to the observed data set(s), and, (iii) Having access to ample amounts of time series data sets from which a robust generative neural network model can be trained. However, for many practical problems that work with time series data in the industry: (i) One usually does not have access to a robust physical model, (ii) The addition of noise can in of itself require large or difficult assumptions (for example, what probability distribution should be used? Or, how large should the noise variance be?), and, (iii) In practice, it can be difficult to source a large representative time series data base with which to train the neural network model for the underlying problem. In this paper, we propose a methodology which attempts to simultaneously tackle all three of these previous limitations to a large extent. The method relies upon the well-studied matrix differential geometry of the Stiefel manifold, as it proposes a simple way in which time series signals can placed on, and then smoothly perturbed over the manifold. We attempt to clarify how this method works by showcasing several potential use cases which in particular work to take advantage of the unique properties of this underlying manifold.

Many-Body Approximation for Tensors

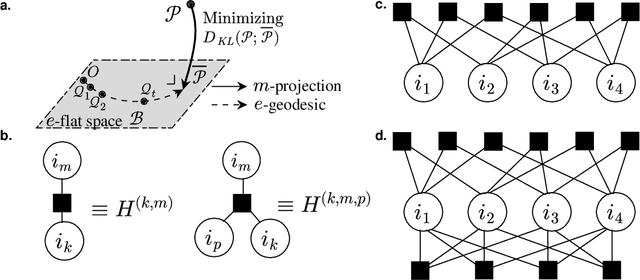
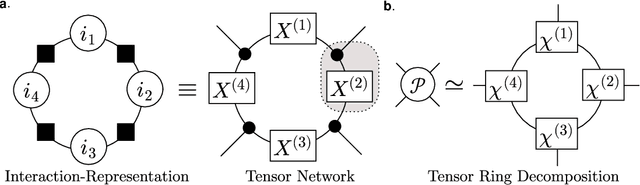
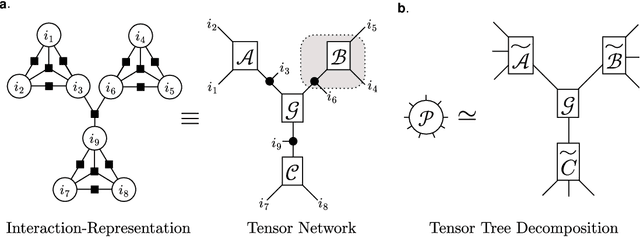
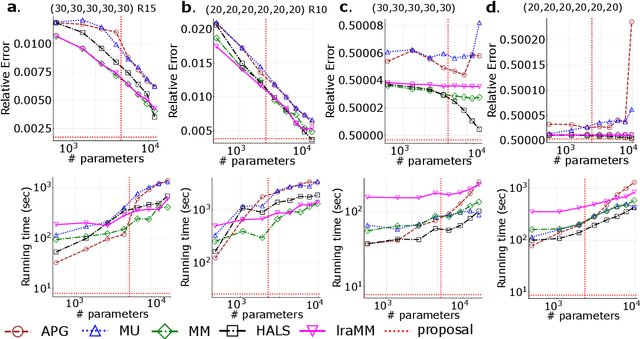
We propose a nonnegative tensor decomposition with focusing on the relationship between the modes of tensors. Traditional decomposition methods assume low-rankness in the representation, resulting in difficulties in global optimization and target rank selection. To address these problems, we present an alternative way to decompose tensors, a many-body approximation for tensors, based on an information geometric formulation. A tensor is treated via an energy-based model, where the tensor and its mode correspond to a probability distribution and a random variable, respectively, and many-body approximation is performed on it by taking the interaction between variables into account. Our model can be globally optimized in polynomial time in terms of the KL divergence minimization, which is empirically faster than low-rank approximations keeping comparable reconstruction error. Furthermore, we visualize interactions between modes as tensor networks and reveal a nontrivial relationship between many-body approximation and low-rank approximation.

A Neural Tangent Kernel Formula for Ensembles of Soft Trees with Arbitrary Architectures

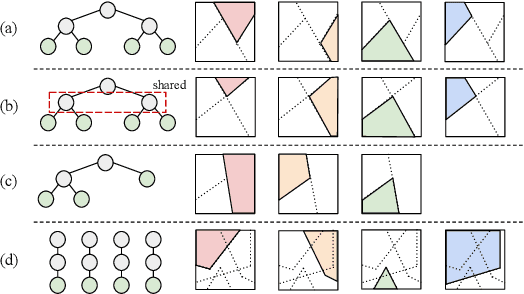
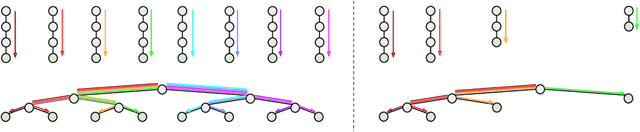
A soft tree is an actively studied variant of a decision tree that updates splitting rules using the gradient method. Although it can have various tree architectures, the theoretical properties of their impact are not well known. In this paper, we formulate and analyze the Neural Tangent Kernel (NTK) induced by soft tree ensembles for arbitrary tree architectures. This kernel leads to the remarkable finding that only the number of leaves at each depth is relevant for the tree architecture in ensemble learning with infinitely many trees. In other words, if the number of leaves at each depth is fixed, the training behavior in function space and the generalization performance are exactly the same across different tree architectures, even if they are not isomorphic. We also show that the NTK of asymmetric trees like decision lists does not degenerate when they get infinitely deep. This is in contrast to the perfect binary trees, whose NTK is known to degenerate and leads to worse generalization performance for deeper trees.