Linear Mode Connectivity in Differentiable Tree Ensembles

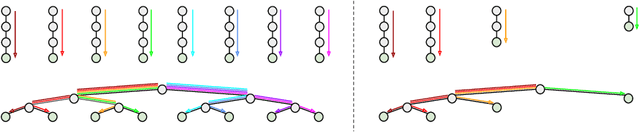
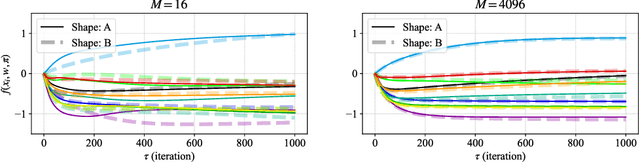
Linear Mode Connectivity (LMC) refers to the phenomenon that performance remains consistent for linearly interpolated models in the parameter space. For independently optimized model pairs from different random initializations, achieving LMC is considered crucial for validating the stable success of the non-convex optimization in modern machine learning models and for facilitating practical parameter-based operations such as model merging. While LMC has been achieved for neural networks by considering the permutation invariance of neurons in each hidden layer, its attainment for other models remains an open question. In this paper, we first achieve LMC for soft tree ensembles, which are tree-based differentiable models extensively used in practice. We show the necessity of incorporating two invariances: subtree flip invariance and splitting order invariance, which do not exist in neural networks but are inherent to tree architectures, in addition to permutation invariance of trees. Moreover, we demonstrate that it is even possible to exclude such additional invariances while keeping LMC by designing decision list-based tree architectures, where such invariances do not exist by definition. Our findings indicate the significance of accounting for architecture-specific invariances in achieving LMC.

A Neural Tangent Kernel Formula for Ensembles of Soft Trees with Arbitrary Architectures

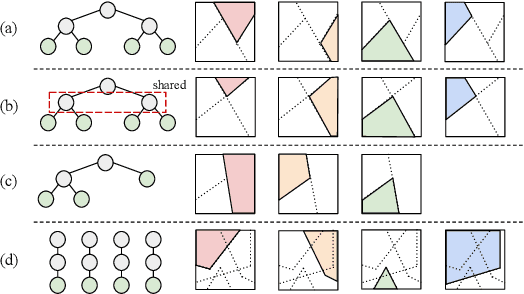
A soft tree is an actively studied variant of a decision tree that updates splitting rules using the gradient method. Although it can have various tree architectures, the theoretical properties of their impact are not well known. In this paper, we formulate and analyze the Neural Tangent Kernel (NTK) induced by soft tree ensembles for arbitrary tree architectures. This kernel leads to the remarkable finding that only the number of leaves at each depth is relevant for the tree architecture in ensemble learning with infinitely many trees. In other words, if the number of leaves at each depth is fixed, the training behavior in function space and the generalization performance are exactly the same across different tree architectures, even if they are not isomorphic. We also show that the NTK of asymmetric trees like decision lists does not degenerate when they get infinitely deep. This is in contrast to the perfect binary trees, whose NTK is known to degenerate and leads to worse generalization performance for deeper trees.

A Neural Tangent Kernel Perspective of Infinite Tree Ensembles

In practical situations, the ensemble tree model is one of the most popular models along with neural networks. A soft tree is one of the variants of a decision tree. Instead of using a greedy method for searching splitting rules, the soft tree is trained using a gradient method in which the whole splitting operation is formulated in a differentiable form. Although ensembles of such soft trees have been increasingly used in recent years, little theoretical work has been done for understanding their behavior. In this paper, by considering an ensemble of infinite soft trees, we introduce and study the Tree Neural Tangent Kernel (TNTK), which provides new insights into the behavior of the infinite ensemble of soft trees. Using the TNTK, we succeed in theoretically finding several non-trivial properties, such as the effect of the oblivious tree structure and the degeneracy of the TNTK induced by the deepening of the trees. Moreover, we empirically examine the performance of an ensemble of infinite soft trees using the TNTK.

Interpretable Mixture Density Estimation by use of Differentiable Tree-module

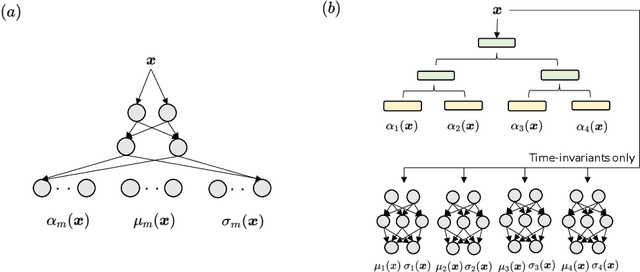
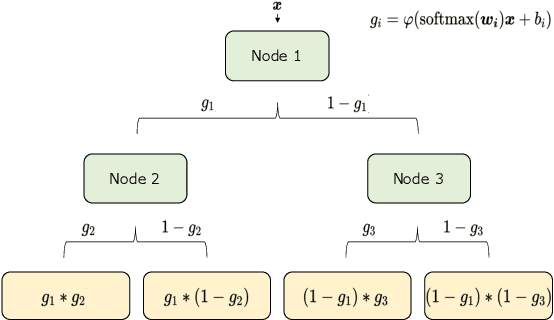
In order to develop reliable services using machine learning, it is important to understand the uncertainty of the model outputs. Often the probability distribution that the prediction target follows has a complex shape, and a mixture distribution is assumed as a distribution that uncertainty follows. Since the output of mixture density estimation is complicated, its interpretability becomes important when considering its use in real services. In this paper, we propose a method for mixture density estimation that utilizes an interpretable tree structure. Further, a fast inference procedure based on time-invariant information cache achieves both high speed and interpretability.

Unintended Effects on Adaptive Learning Rate for Training Neural Network with Output Scale Change

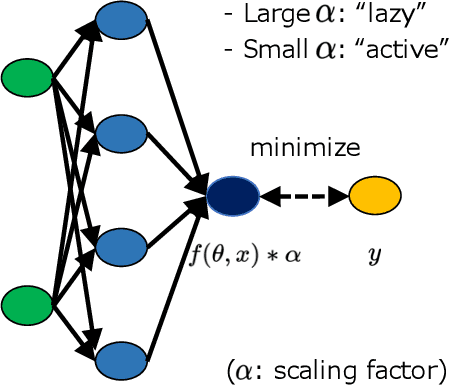
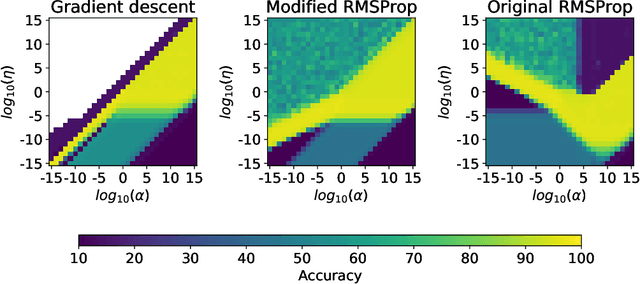
A multiplicative constant scaling factor is often applied to the model output to adjust the dynamics of neural network parameters. This has been used as one of the key interventions in an empirical study of lazy and active behavior. However, we show that the combination of such scaling and a commonly used adaptive learning rate optimizer strongly affects the training behavior of the neural network. This is problematic as it can cause \emph{unintended behavior} of neural networks, resulting in the misinterpretation of experimental results. Specifically, for some scaling settings, the effect of the adaptive learning rate disappears or is strongly influenced by the scaling factor. To avoid the unintended effect, we present a modification of an optimization algorithm and demonstrate remarkable differences between adaptive learning rate optimization and simple gradient descent, especially with a small ($<1.0$) scaling factor.