A Neural Tangent Kernel Formula for Ensembles of Soft Trees with Arbitrary Architectures
Paper and Code
May 25, 2022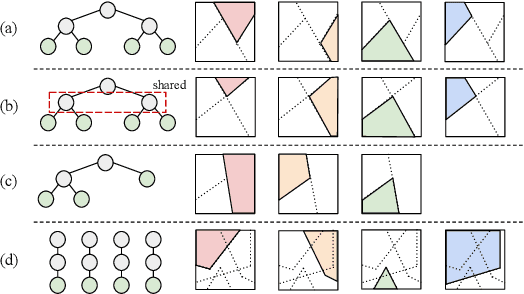
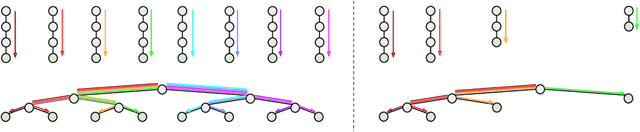

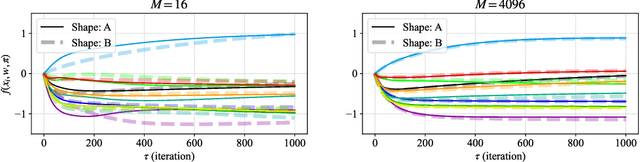
A soft tree is an actively studied variant of a decision tree that updates splitting rules using the gradient method. Although it can have various tree architectures, the theoretical properties of their impact are not well known. In this paper, we formulate and analyze the Neural Tangent Kernel (NTK) induced by soft tree ensembles for arbitrary tree architectures. This kernel leads to the remarkable finding that only the number of leaves at each depth is relevant for the tree architecture in ensemble learning with infinitely many trees. In other words, if the number of leaves at each depth is fixed, the training behavior in function space and the generalization performance are exactly the same across different tree architectures, even if they are not isomorphic. We also show that the NTK of asymmetric trees like decision lists does not degenerate when they get infinitely deep. This is in contrast to the perfect binary trees, whose NTK is known to degenerate and leads to worse generalization performance for deeper trees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge