StiefelGen: A Simple, Model Agnostic Approach for Time Series Data Augmentation over Riemannian Manifolds

Data augmentation is an area of research which has seen active development in many machine learning fields, such as in image-based learning models, reinforcement learning for self driving vehicles, and general noise injection for point cloud data. However, convincing methods for general time series data augmentation still leaves much to be desired, especially since the methods developed for these models do not readily cross-over. Three common approaches for time series data augmentation include: (i) Constructing a physics-based model and then imbuing uncertainty over the coefficient space (for example), (ii) Adding noise to the observed data set(s), and, (iii) Having access to ample amounts of time series data sets from which a robust generative neural network model can be trained. However, for many practical problems that work with time series data in the industry: (i) One usually does not have access to a robust physical model, (ii) The addition of noise can in of itself require large or difficult assumptions (for example, what probability distribution should be used? Or, how large should the noise variance be?), and, (iii) In practice, it can be difficult to source a large representative time series data base with which to train the neural network model for the underlying problem. In this paper, we propose a methodology which attempts to simultaneously tackle all three of these previous limitations to a large extent. The method relies upon the well-studied matrix differential geometry of the Stiefel manifold, as it proposes a simple way in which time series signals can placed on, and then smoothly perturbed over the manifold. We attempt to clarify how this method works by showcasing several potential use cases which in particular work to take advantage of the unique properties of this underlying manifold.

A Geometric Look at Double Descent Risk: Volumes, Singularities, and Distinguishabilities

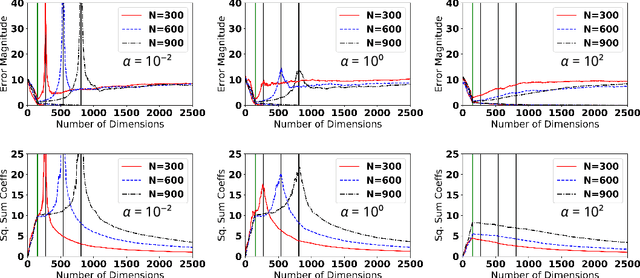
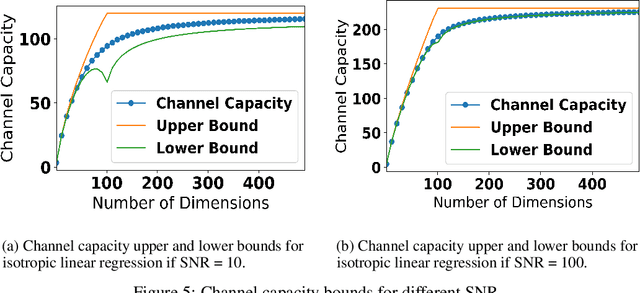
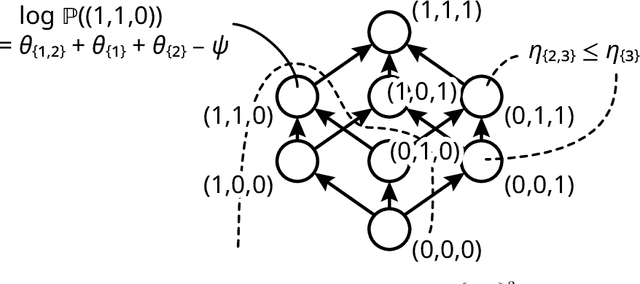
The appearance of the double-descent risk phenomenon has received growing interest in the machine learning and statistics community, as it challenges well-understood notions behind the U-shaped train-test curves. Motivated through Rissanen's minimum description length (MDL), Balasubramanian's Occam's Razor, and Amari's information geometry, we investigate how the logarithm of the model volume: $\log V$, works to extend intuition behind the AIC and BIC model selection criteria. We find that for the particular model classes of isotropic linear regression, statistical lattices, and the stochastic perceptron unit, the $\log V$ term may be decomposed into a sum of distinct components. These components work to extend the idea of model complexity inherent in AIC and BIC, and are driven by new, albeit intuitive notions of (i) Model richness, and (ii) Model distinguishability. Our theoretical analysis assists in the understanding of how the double descent phenomenon may manifest, as well as why generalization error does not necessarily continue to grow with increasing model dimensionality.

A Tensor-based Structural Health Monitoring Approach for Aeroservoelastic Systems

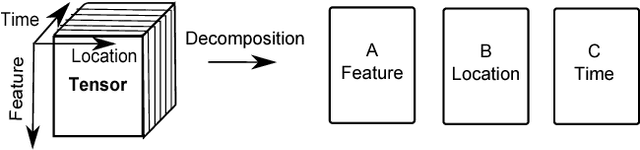
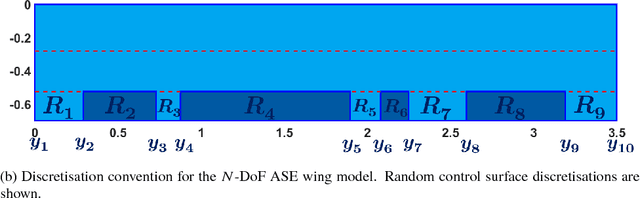
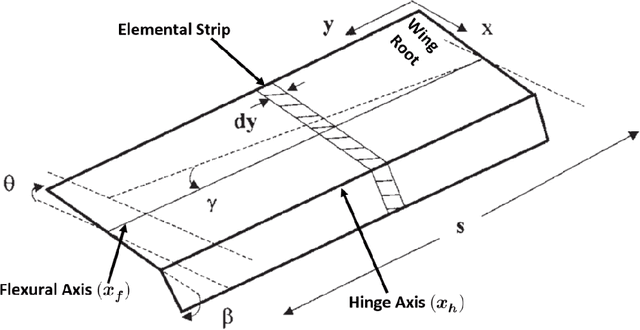
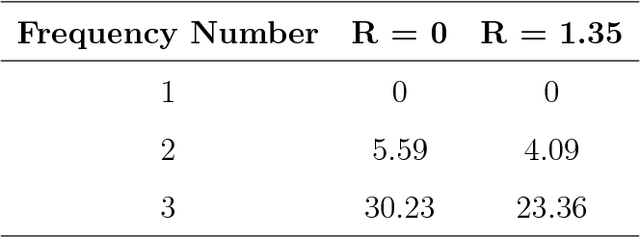
Structural health monitoring is a condition-based field of study utilised to monitor infrastructure, via sensing systems. It is therefore used in the field of aerospace engineering to assist in monitoring the health of aerospace structures. A difficulty however is that in structural health monitoring the data input is usually from sensor arrays, which results in data which are highly redundant and correlated, an area in which traditional two-way matrix approaches have had difficulty in deconstructing and interpreting. Newer methods involving tensor analysis allow us to analyse this multi-way structural data in a coherent manner. In our approach, we demonstrate the usefulness of tensor-based learning coupled with for damage detection, on a novel $N$-DoF Lagrangian aeroservoelastic model.

New Approaches to Inverse Structural Modification Theory using Random Projections

In many contexts the modal properties of a structure change, either due to the impact of a changing environment, fatigue, or due to the presence of structural damage. For example during flight, an aircraft's modal properties are known to change with both altitude and velocity. It is thus important to quantify these changes given only a truncated set of modal data, which is usually the case experimentally. This procedure is formally known as the generalised inverse eigenvalue problem. In this paper we experimentally show that first-order gradient-based methods that optimise objective functions defined over a modal are prohibitive due to the required small step sizes. This in turn leads to the justification of using a non-gradient, black box optimiser in the form of particle swarm optimisation. We further show how it is possible to solve such inverse eigenvalue problems in a lower dimensional space by the use of random projections, which in many cases reduces the total dimensionality of the optimisation problem by 80% to 99%. Two example problems are explored involving a ten-dimensional mass-stiffness toy problem, and a one-dimensional finite element mass-stiffness approximation for a Boeing 737-300 aircraft.