A Geometric Look at Double Descent Risk: Volumes, Singularities, and Distinguishabilities

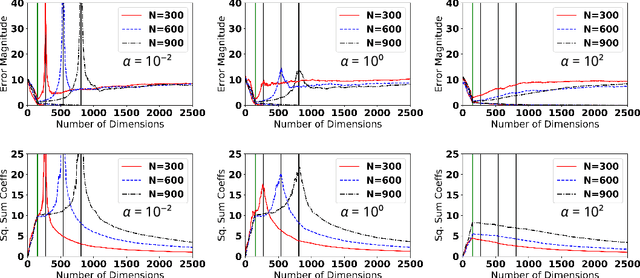
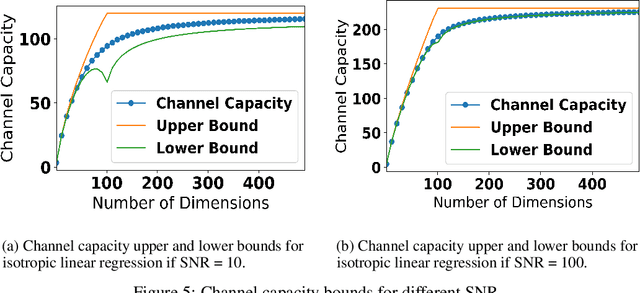
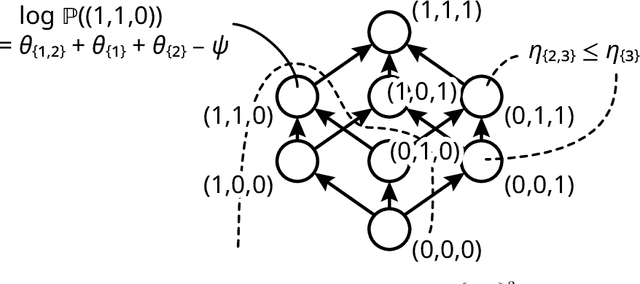
The appearance of the double-descent risk phenomenon has received growing interest in the machine learning and statistics community, as it challenges well-understood notions behind the U-shaped train-test curves. Motivated through Rissanen's minimum description length (MDL), Balasubramanian's Occam's Razor, and Amari's information geometry, we investigate how the logarithm of the model volume: $\log V$, works to extend intuition behind the AIC and BIC model selection criteria. We find that for the particular model classes of isotropic linear regression, statistical lattices, and the stochastic perceptron unit, the $\log V$ term may be decomposed into a sum of distinct components. These components work to extend the idea of model complexity inherent in AIC and BIC, and are driven by new, albeit intuitive notions of (i) Model richness, and (ii) Model distinguishability. Our theoretical analysis assists in the understanding of how the double descent phenomenon may manifest, as well as why generalization error does not necessarily continue to grow with increasing model dimensionality.