A Complete Decomposition of KL Error using Refined Information and Mode Interaction Selection

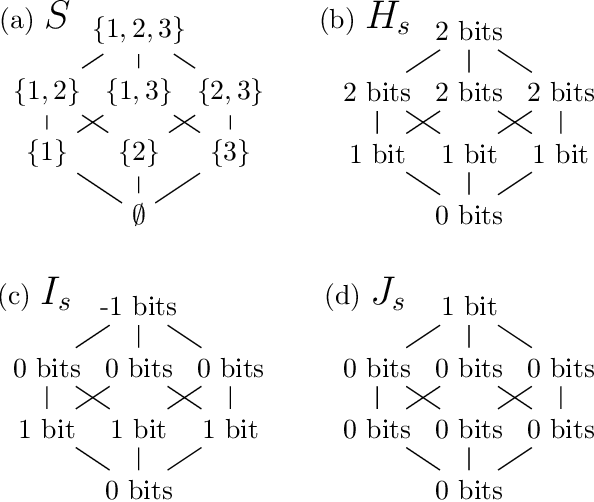
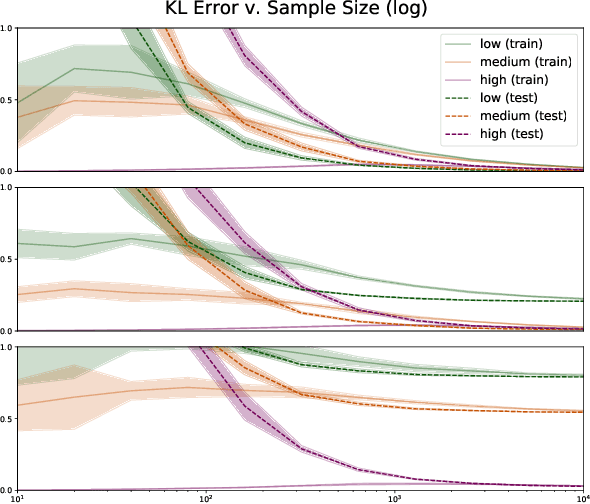
The log-linear model has received a significant amount of theoretical attention in previous decades and remains the fundamental tool used for learning probability distributions over discrete variables. Despite its large popularity in statistical mechanics and high-dimensional statistics, the vast majority of such energy-based modeling approaches only focus on the two-variable relationships, such as Boltzmann machines and Markov graphical models. Although these approaches have easier-to-solve structure learning problems and easier-to-optimize parametric distributions, they often ignore the rich structure which exists in the higher-order interactions between different variables. Using more recent tools from the field of information geometry, we revisit the classical formulation of the log-linear model with a focus on higher-order mode interactions, going beyond the 1-body modes of independent distributions and the 2-body modes of Boltzmann distributions. This perspective allows us to define a complete decomposition of the KL error. This then motivates the formulation of a sparse selection problem over the set of possible mode interactions. In the same way as sparse graph selection allows for better generalization, we find that our learned distributions are able to more efficiently use the finite amount of data which is available in practice. On both synthetic and real-world datasets, we demonstrate our algorithm's effectiveness in maximizing the log-likelihood for the generative task and also the ease of adaptability to the discriminative task of classification.