Non-negative Tensor Mixture Learning for Discrete Density Estimation

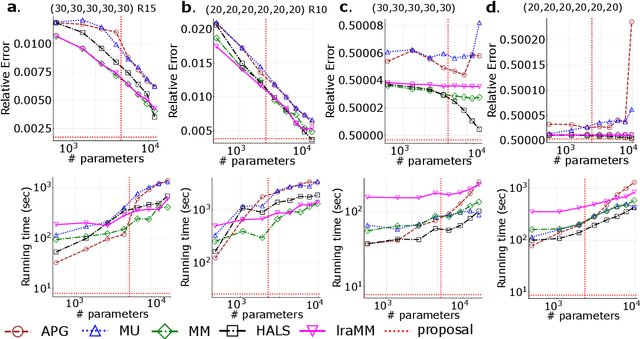
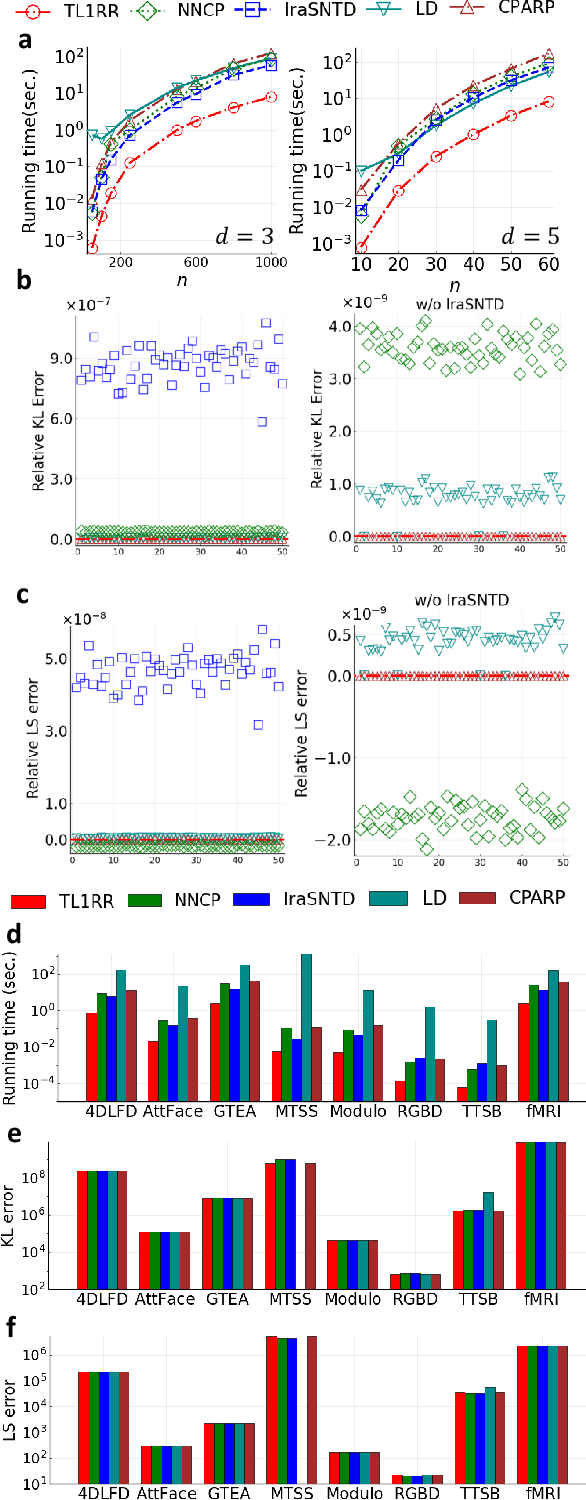
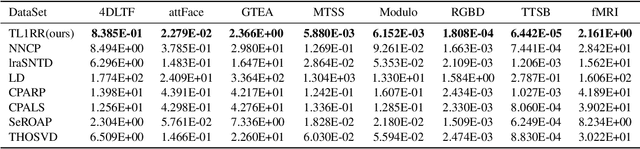
We present an expectation-maximization (EM) based unified framework for non-negative tensor decomposition that optimizes the Kullback-Leibler divergence. To avoid iterations in each M-step and learning rate tuning, we establish a general relationship between low-rank decomposition and many-body approximation. Using this connection, we exploit that the closed-form solution of the many-body approximation can be used to update all parameters simultaneously in the M-step. Our framework not only offers a unified methodology for a variety of low-rank structures, including CP, Tucker, and Train decompositions, but also their combinations forming mixtures of tensors as well as robust adaptive noise modeling. Empirically, we demonstrate that our framework provides superior generalization for discrete density estimation compared to conventional tensor-based approaches.

Many-Body Approximation for Tensors

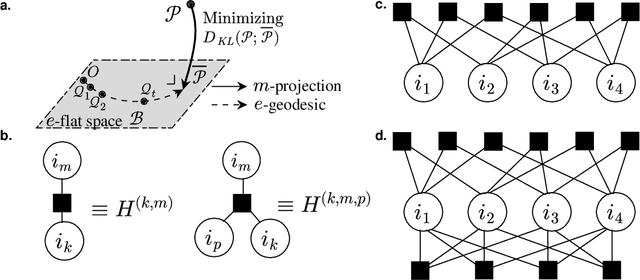
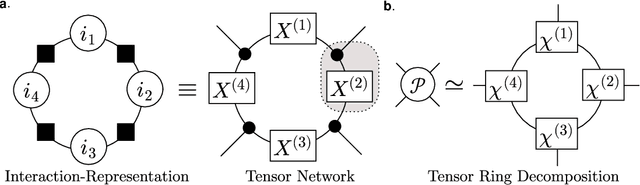
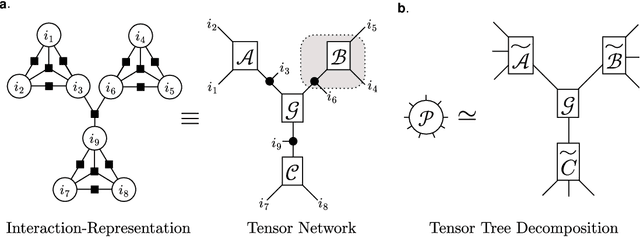
We propose a nonnegative tensor decomposition with focusing on the relationship between the modes of tensors. Traditional decomposition methods assume low-rankness in the representation, resulting in difficulties in global optimization and target rank selection. To address these problems, we present an alternative way to decompose tensors, a many-body approximation for tensors, based on an information geometric formulation. A tensor is treated via an energy-based model, where the tensor and its mode correspond to a probability distribution and a random variable, respectively, and many-body approximation is performed on it by taking the interaction between variables into account. Our model can be globally optimized in polynomial time in terms of the KL divergence minimization, which is empirically faster than low-rank approximations keeping comparable reconstruction error. Furthermore, we visualize interactions between modes as tensor networks and reveal a nontrivial relationship between many-body approximation and low-rank approximation.

Fast Rank-1 NMF for Missing Data with KL Divergence

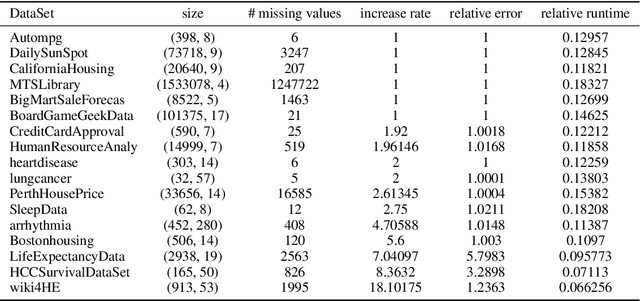
We propose a fast non-gradient based method of rank-1 non-negative matrix factorization (NMF) for missing data, called A1GM, that minimizes the KL divergence from an input matrix to the reconstructed rank-1 matrix. Our method is based on our new finding of an analytical closed-formula of the best rank-1 non-negative multiple matrix factorization (NMMF), a variety of NMF. NMMF is known to exactly solve NMF for missing data if positions of missing values satisfy a certain condition, and A1GM transforms a given matrix so that the analytical solution to NMMF can be applied. We empirically show that A1GM is more efficient than a gradient method with competitive reconstruction errors.

A Closed Form Solution to Best Rank-1 Tensor Approximation via KL divergence Minimization

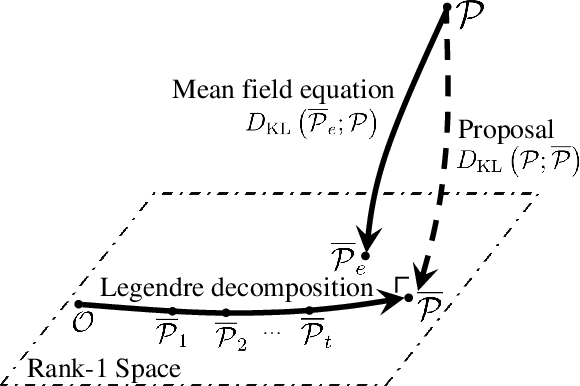
Tensor decomposition is a fundamentally challenging problem. Even the simplest case of tensor decomposition, the rank-1 approximation in terms of the Least Squares (LS) error, is known to be NP-hard. Here, we show that, if we consider the KL divergence instead of the LS error, we can analytically derive a closed form solution for the rank-1 tensor that minimizes the KL divergence from a given positive tensor. Our key insight is to treat a positive tensor as a probability distribution and formulate the process of rank-1 approximation as a projection onto the set of rank-1 tensors. This enables us to solve rank-1 approximation by convex optimization. We empirically demonstrate that our algorithm is an order of magnitude faster than the existing rank-1 approximation methods and gives better approximation of given tensors, which supports our theoretical finding.

Rank Reduction, Matrix Balancing, and Mean-Field Approximation on Statistical Manifold

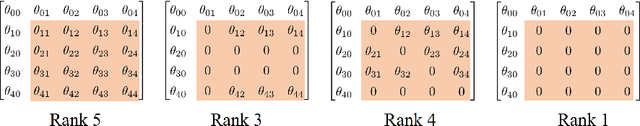
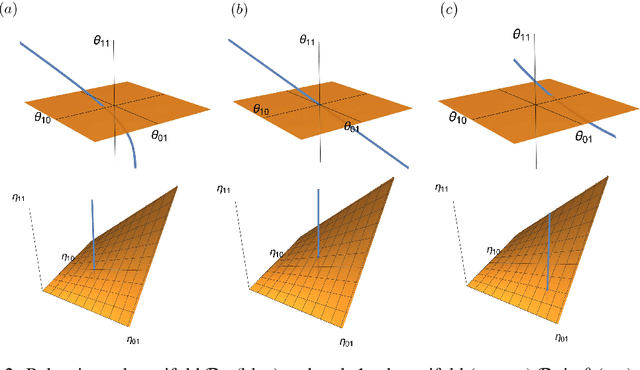
We present a unified view of three different problems; rank reduction of matrices, matrix balancing, and mean-field approximation, using information geometry. Our key idea is to treat each matrix as a probability distribution represented by a loglinear model on a partially ordered set (poset), which enables us to formulate rank reduction and balancing of a matrix as projection onto a statistical submanifold, which corresponds to the set of low-rank matrices or that of balanced matrices. Moreover, the process of rank-1 reduction coincides with the mean-field approximation in the sense that the expectation parameters can be decomposed into products, where the mean-field equation holds. Our observation leads to a new convex optimization formulation of rank reduction, which applies to any nonnegative matrices, while the Nystr\"om method, one of the most popular rank reduction methods, is applicable to only kernel positive semidefinite matrices. We empirically show that our rank reduction method achieves better approximation of matrices produced by real-world data compared to Nystrom method.