Rank Reduction, Matrix Balancing, and Mean-Field Approximation on Statistical Manifold

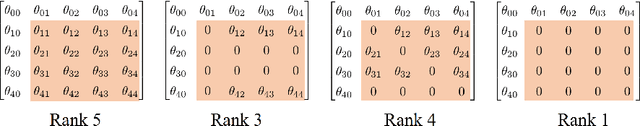
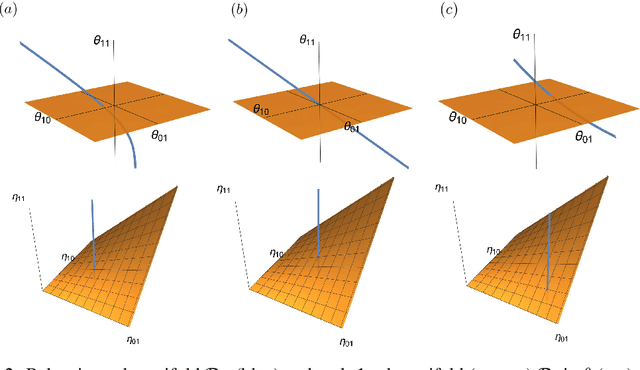
We present a unified view of three different problems; rank reduction of matrices, matrix balancing, and mean-field approximation, using information geometry. Our key idea is to treat each matrix as a probability distribution represented by a loglinear model on a partially ordered set (poset), which enables us to formulate rank reduction and balancing of a matrix as projection onto a statistical submanifold, which corresponds to the set of low-rank matrices or that of balanced matrices. Moreover, the process of rank-1 reduction coincides with the mean-field approximation in the sense that the expectation parameters can be decomposed into products, where the mean-field equation holds. Our observation leads to a new convex optimization formulation of rank reduction, which applies to any nonnegative matrices, while the Nystr\"om method, one of the most popular rank reduction methods, is applicable to only kernel positive semidefinite matrices. We empirically show that our rank reduction method achieves better approximation of matrices produced by real-world data compared to Nystrom method.