Many-Body Approximation for Tensors
Paper and Code
Sep 30, 2022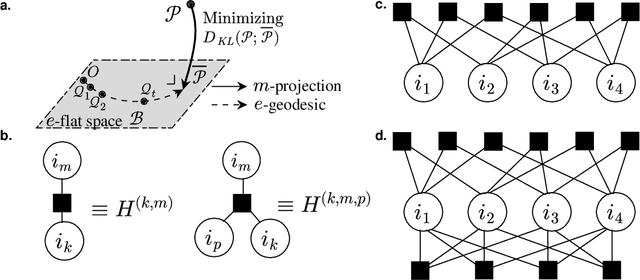
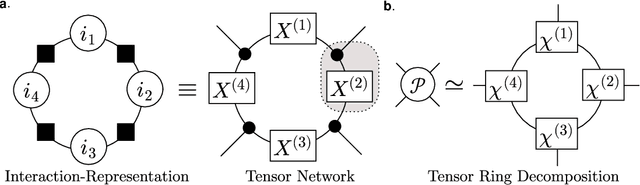
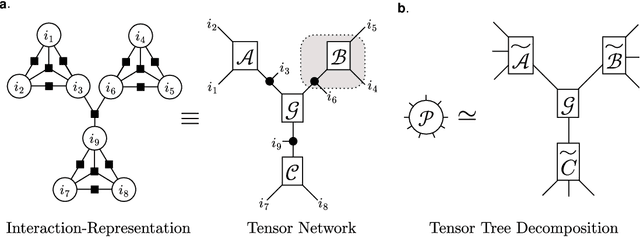
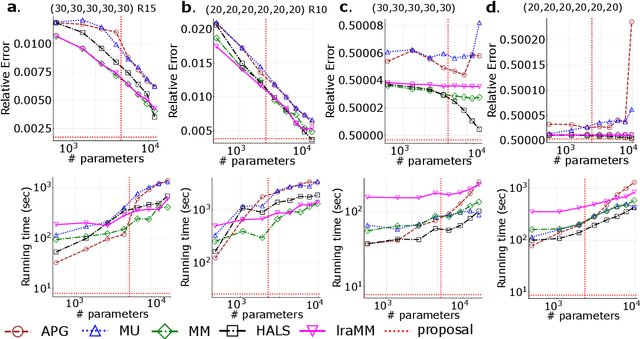
We propose a nonnegative tensor decomposition with focusing on the relationship between the modes of tensors. Traditional decomposition methods assume low-rankness in the representation, resulting in difficulties in global optimization and target rank selection. To address these problems, we present an alternative way to decompose tensors, a many-body approximation for tensors, based on an information geometric formulation. A tensor is treated via an energy-based model, where the tensor and its mode correspond to a probability distribution and a random variable, respectively, and many-body approximation is performed on it by taking the interaction between variables into account. Our model can be globally optimized in polynomial time in terms of the KL divergence minimization, which is empirically faster than low-rank approximations keeping comparable reconstruction error. Furthermore, we visualize interactions between modes as tensor networks and reveal a nontrivial relationship between many-body approximation and low-rank approximation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge