Non-negative Tensor Mixture Learning for Discrete Density Estimation

We present an expectation-maximization (EM) based unified framework for non-negative tensor decomposition that optimizes the Kullback-Leibler divergence. To avoid iterations in each M-step and learning rate tuning, we establish a general relationship between low-rank decomposition and many-body approximation. Using this connection, we exploit that the closed-form solution of the many-body approximation can be used to update all parameters simultaneously in the M-step. Our framework not only offers a unified methodology for a variety of low-rank structures, including CP, Tucker, and Train decompositions, but also their combinations forming mixtures of tensors as well as robust adaptive noise modeling. Empirically, we demonstrate that our framework provides superior generalization for discrete density estimation compared to conventional tensor-based approaches.

Probabilistic Block Term Decomposition for the Modelling of Higher-Order Arrays

Tensors are ubiquitous in science and engineering and tensor factorization approaches have become important tools for the characterization of higher order structure. Factorizations includes the outer-product rank Canonical Polyadic Decomposition (CPD) as well as the multi-linear rank Tucker decomposition in which the Block-Term Decomposition (BTD) is a structured intermediate interpolating between these two representations. Whereas CPD, Tucker, and BTD have traditionally relied on maximum-likelihood estimation, Bayesian inference has been use to form probabilistic CPD and Tucker. We propose, an efficient variational Bayesian probabilistic BTD, which uses the von-Mises Fisher matrix distribution to impose orthogonality in the multi-linear Tucker parts forming the BTD. On synthetic and two real datasets, we highlight the Bayesian inference procedure and demonstrate using the proposed pBTD on noisy data and for model order quantification. We find that the probabilistic BTD can quantify suitable multi-linear structures providing a means for robust inference of patterns in multi-linear data.

PARAFAC2$\times$N: Coupled Decomposition of Multi-modal Data with Drift in N Modes

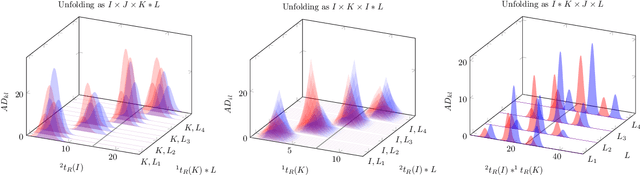
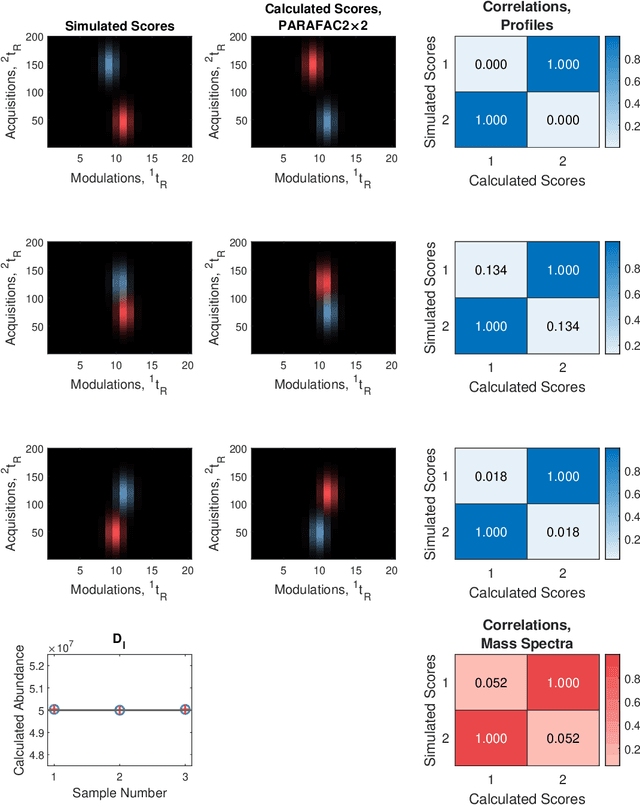
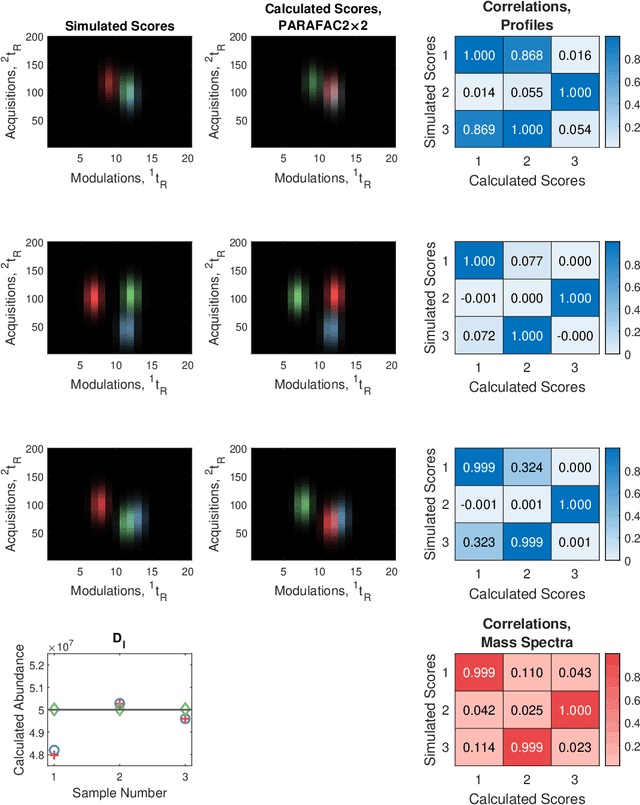
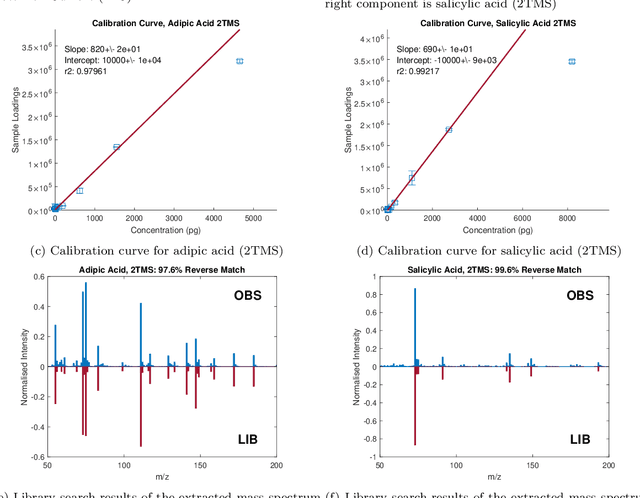
Reliable analysis of comprehensive two-dimensional gas chromatography - time-of-flight mass spectrometry (GC$\times$GC-TOFMS) data is considered to be a major bottleneck for its widespread application. For multiple samples, GC$\times$GC-TOFMS data for specific chromatographic regions manifests as a 4th order tensor of I mass spectral acquisitions, J mass channels, K modulations, and L samples. Chromatographic drift is common along both the first-dimension (modulations), and along the second-dimension (mass spectral acquisitions), while drift along the mass channel and sample dimensions is for all practical purposes nonexistent. A number of solutions to handling GC$\times$GC-TOFMS data have been proposed: these involve reshaping the data to make it amenable to either 2nd order decomposition techniques based on Multivariate Curve Resolution (MCR), or 3rd order decomposition techniques such as Parallel Factor Analysis 2 (PARAFAC2). PARAFAC2 has been utilised to model chromatographic drift along one mode, which has enabled its use for robust decomposition of multiple GC-MS experiments. Although extensible, it is not straightforward to implement a PARAFAC2 model that accounts for drift along multiple modes. In this submission, we demonstrate a new approach and a general theory for modelling data with drift along multiple modes, for applications in multidimensional chromatography with multivariate detection.