James J. Harynuk
Untargeted Region of Interest Selection for GC-MS Data using a Pseudo F-Ratio Moving Window ($ψ$FRMV)
Jul 30, 2022



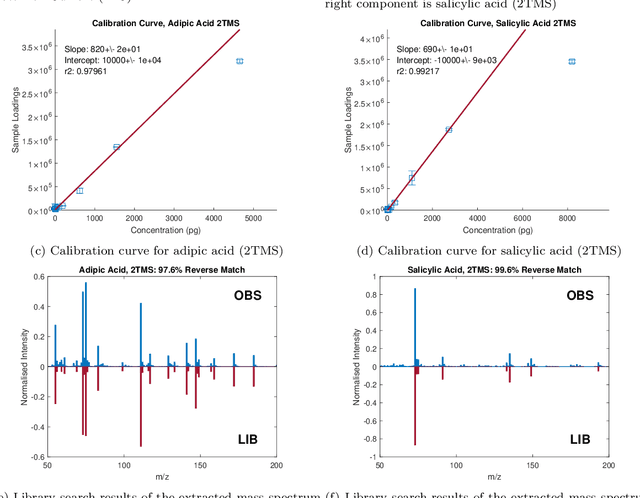
Abstract:There are many challenges associated with analysing gas chromatography - mass spectrometry (GC-MS) data. Many of these challenges stem from the fact that electron ionisation can make it difficult to recover molecular information due to the high degree of fragmentation with concomitant loss of molecular ion signal. With GC-MS data there are often many common fragment ions shared among closely-eluting peaks, necessitating sophisticated methods for analysis. Some of these methods are fully automated, but make some assumptions about the data which can introduce artifacts during the analysis. Chemometric methods such as Multivariate Curve Resolution, or Parallel Factor Analysis are particularly attractive, since they are flexible and make relatively few assumptions about the data - ideally resulting in fewer artifacts. These methods do require expert user intervention to determine the most relevant regions of interest and an appropriate number of components, $k$, for each region. Automated region of interest selection is needed to permit automated batch processing of chromatographic data with advanced signal deconvolution. Here, we propose a new method for automated, untargeted region of interest selection that accounts for the multivariate information present in GC-MS data to select regions of interest based on the ratio of the squared first, and second singular values from the Singular Value Decomposition of a window that moves across the chromatogram. Assuming that the first singular value accounts largely for signal, and that the second singular value accounts largely for noise, it is possible to interpret the relationship between these two values as a probabilistic distribution of Fisher Ratios. The sensitivity of the algorithm was tested by investigating the concentration at which the algorithm can no longer pick out chromatographic regions known to contain signal.
PARAFAC2$\times$N: Coupled Decomposition of Multi-modal Data with Drift in N Modes
May 06, 2022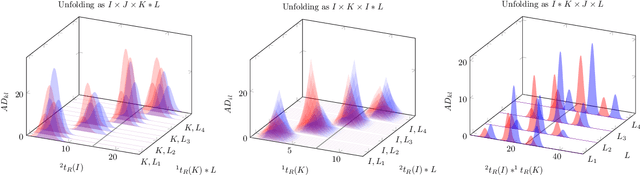
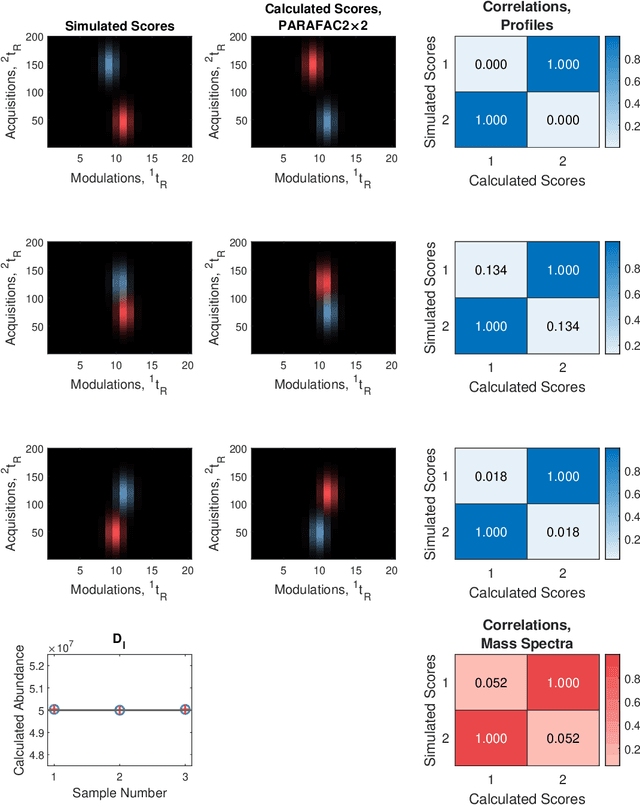
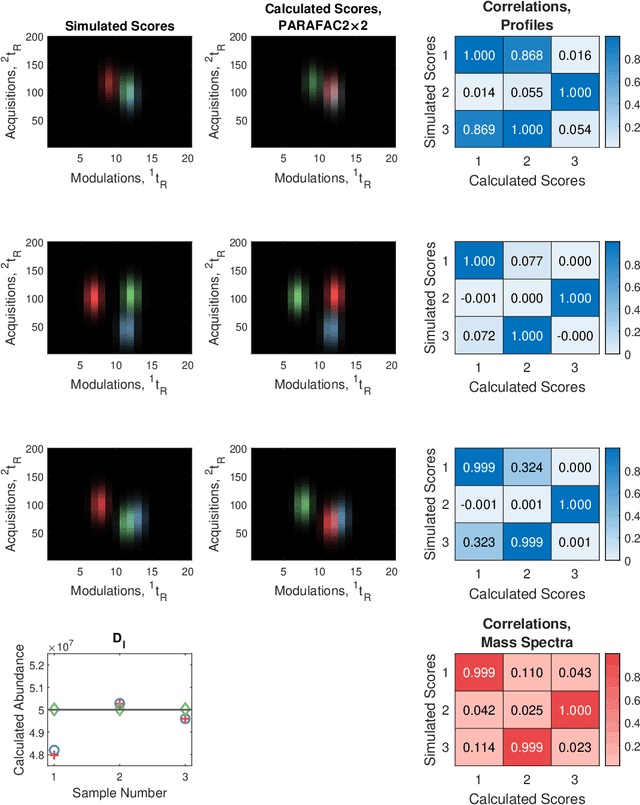
Abstract:Reliable analysis of comprehensive two-dimensional gas chromatography - time-of-flight mass spectrometry (GC$\times$GC-TOFMS) data is considered to be a major bottleneck for its widespread application. For multiple samples, GC$\times$GC-TOFMS data for specific chromatographic regions manifests as a 4th order tensor of I mass spectral acquisitions, J mass channels, K modulations, and L samples. Chromatographic drift is common along both the first-dimension (modulations), and along the second-dimension (mass spectral acquisitions), while drift along the mass channel and sample dimensions is for all practical purposes nonexistent. A number of solutions to handling GC$\times$GC-TOFMS data have been proposed: these involve reshaping the data to make it amenable to either 2nd order decomposition techniques based on Multivariate Curve Resolution (MCR), or 3rd order decomposition techniques such as Parallel Factor Analysis 2 (PARAFAC2). PARAFAC2 has been utilised to model chromatographic drift along one mode, which has enabled its use for robust decomposition of multiple GC-MS experiments. Although extensible, it is not straightforward to implement a PARAFAC2 model that accounts for drift along multiple modes. In this submission, we demonstrate a new approach and a general theory for modelling data with drift along multiple modes, for applications in multidimensional chromatography with multivariate detection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge