PARAFAC2$\times$N: Coupled Decomposition of Multi-modal Data with Drift in N Modes
Paper and Code
May 06, 2022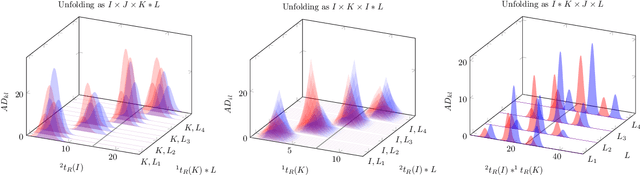
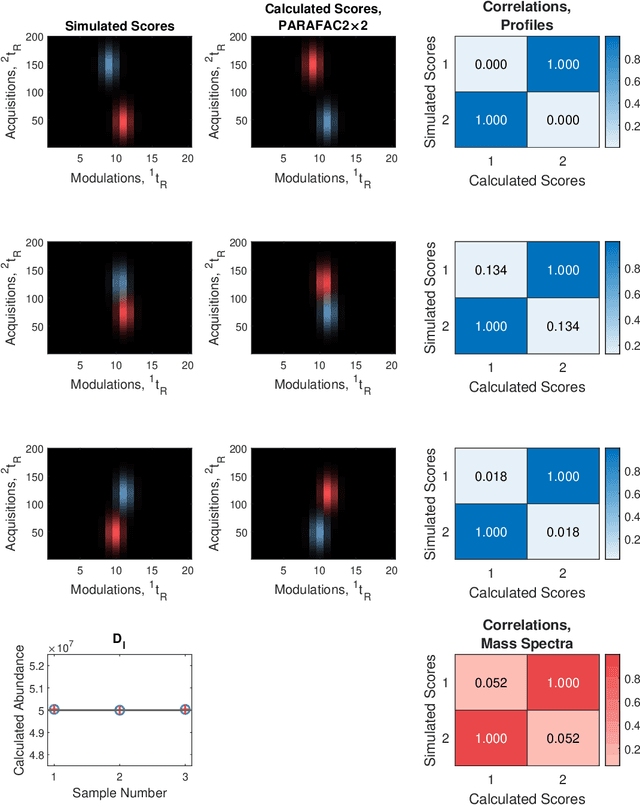
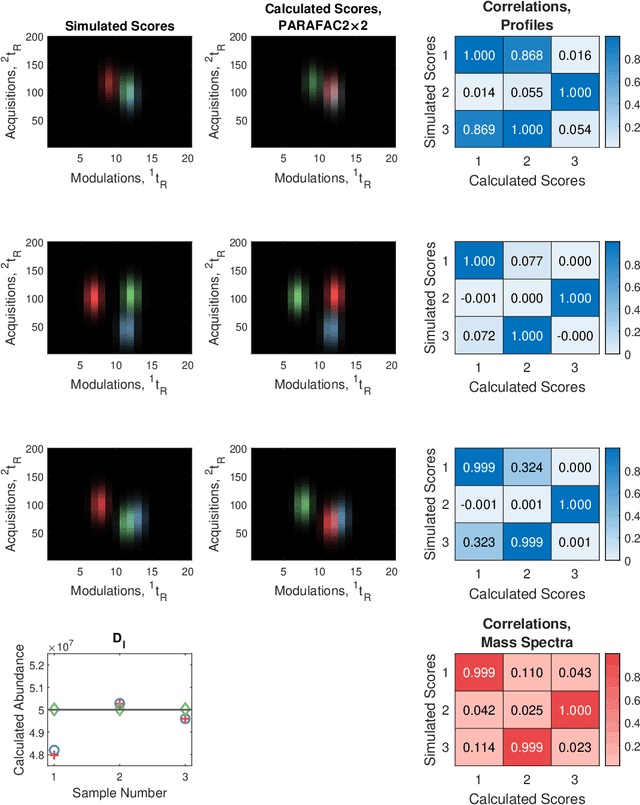
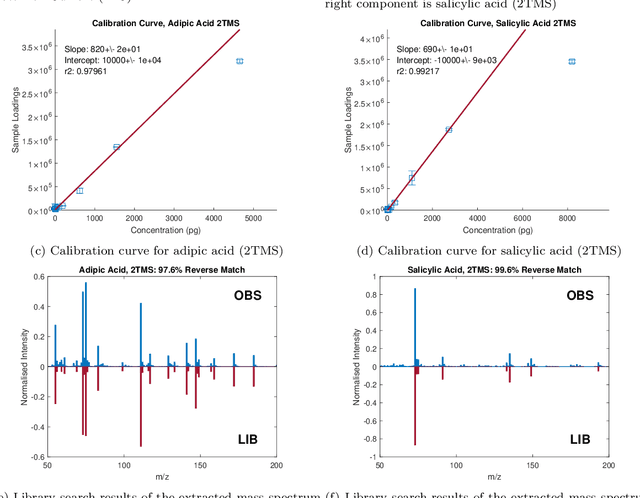
Reliable analysis of comprehensive two-dimensional gas chromatography - time-of-flight mass spectrometry (GC$\times$GC-TOFMS) data is considered to be a major bottleneck for its widespread application. For multiple samples, GC$\times$GC-TOFMS data for specific chromatographic regions manifests as a 4th order tensor of I mass spectral acquisitions, J mass channels, K modulations, and L samples. Chromatographic drift is common along both the first-dimension (modulations), and along the second-dimension (mass spectral acquisitions), while drift along the mass channel and sample dimensions is for all practical purposes nonexistent. A number of solutions to handling GC$\times$GC-TOFMS data have been proposed: these involve reshaping the data to make it amenable to either 2nd order decomposition techniques based on Multivariate Curve Resolution (MCR), or 3rd order decomposition techniques such as Parallel Factor Analysis 2 (PARAFAC2). PARAFAC2 has been utilised to model chromatographic drift along one mode, which has enabled its use for robust decomposition of multiple GC-MS experiments. Although extensible, it is not straightforward to implement a PARAFAC2 model that accounts for drift along multiple modes. In this submission, we demonstrate a new approach and a general theory for modelling data with drift along multiple modes, for applications in multidimensional chromatography with multivariate detection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge