Antti Hyttinen
Binary Independent Component Analysis via Non-stationarity
Nov 30, 2021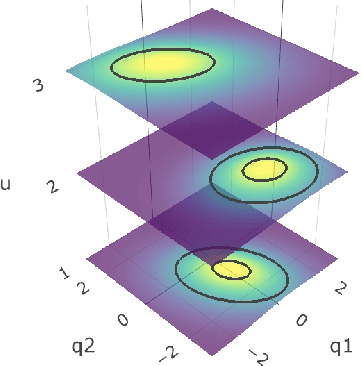
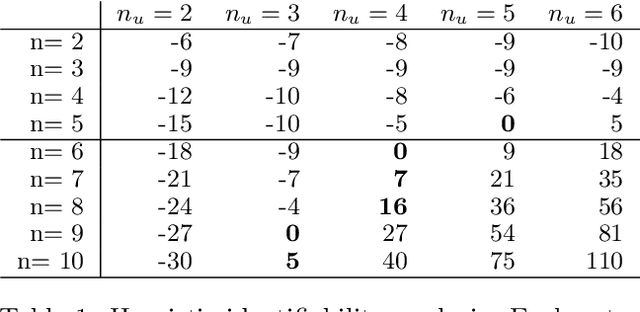
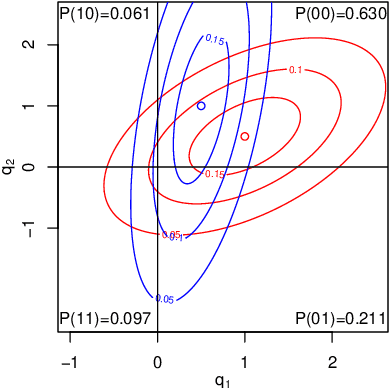
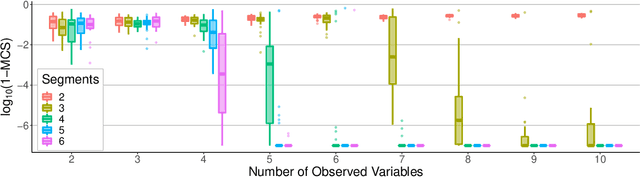
Abstract:We consider independent component analysis of binary data. While fundamental in practice, this case has been much less developed than ICA for continuous data. We start by assuming a linear mixing model in a continuous-valued latent space, followed by a binary observation model. Importantly, we assume that the sources are non-stationary; this is necessary since any non-Gaussianity would essentially be destroyed by the binarization. Interestingly, the model allows for closed-form likelihood by employing the cumulative distribution function of the multivariate Gaussian distribution. In stark contrast to the continuous-valued case, we prove non-identifiability of the model with few observed variables; our empirical results imply identifiability when the number of observed variables is higher. We present a practical method for binary ICA that uses only pairwise marginals, which are faster to compute than the full multivariate likelihood.
Towards Scalable Bayesian Learning of Causal DAGs
Sep 30, 2020


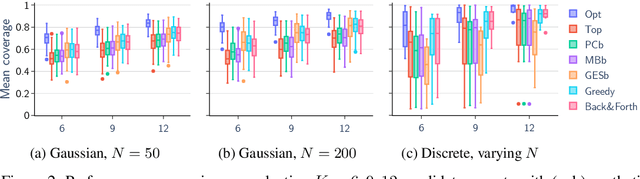
Abstract:We give methods for Bayesian inference of directed acyclic graphs, DAGs, and the induced causal effects from passively observed complete data. Our methods build on a recent Markov chain Monte Carlo scheme for learning Bayesian networks, which enables efficient approximate sampling from the graph posterior, provided that each node is assigned a small number K of candidate parents. We present algorithmic tricks to significantly reduce the space and time requirements of the method, making it feasible to use substantially larger values of K. Furthermore, we investigate the problem of selecting the candidate parents per node so as to maximize the covered posterior mass. Finally, we combine our sampling method with a novel Bayesian approach for estimating causal effects in linear Gaussian DAG models. Numerical experiments demonstrate the performance of our methods in detecting ancestor-descendant relations, and in effect estimation our Bayesian method is shown to outperform existing approaches.
Identifying Causal Effects via Context-specific Independence Relations
Sep 21, 2020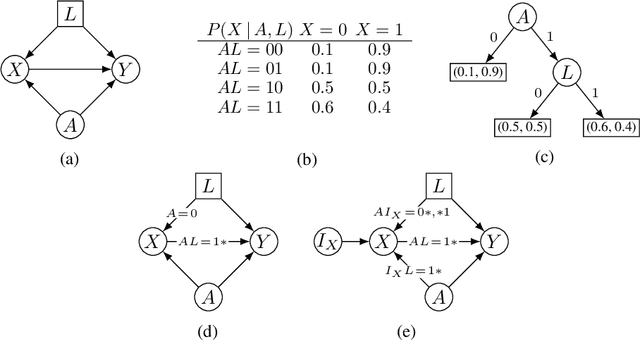
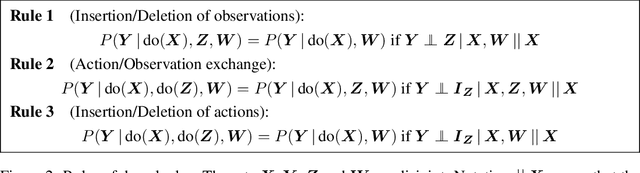

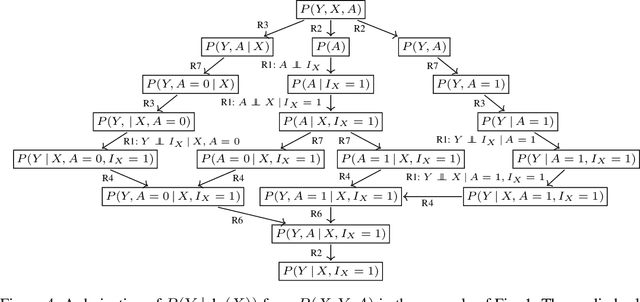
Abstract:Causal effect identification considers whether an interventional probability distribution can be uniquely determined from a passively observed distribution in a given causal structure. If the generating system induces context-specific independence (CSI) relations, the existing identification procedures and criteria based on do-calculus are inherently incomplete. We show that deciding causal effect non-identifiability is NP-hard in the presence of CSIs. Motivated by this, we design a calculus and an automated search procedure for identifying causal effects in the presence of CSIs. The approach is provably sound and it includes standard do-calculus as a special case. With the approach we can obtain identifying formulas that were unobtainable previously, and demonstrate that a small number of CSI-relations may be sufficient to turn a previously non-identifiable instance to identifiable.
Causal Effect Identification from Multiple Incomplete Data Sources: A General Search-based Approach
Feb 28, 2019
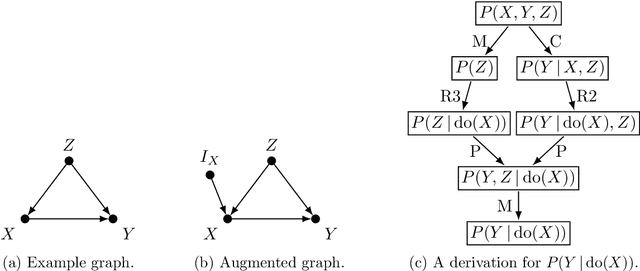

Abstract:Causal effect identification considers whether an interventional probability distribution can be uniquely determined without parametric assumptions from measured source distributions and structural knowledge on the generating system. While complete graphical criteria and procedures exist for many identification problems, there are still challenging but important extensions that have not been considered in the literature. To tackle these new settings, we present a search algorithm directly over the rules of do-calculus. Due to generality of do-calculus, the search is capable of taking more advanced data-generating mechanisms into account along with an arbitrary type of both observational and experimental source distributions. The search is enhanced via a heuristic and search space reduction techniques. The approach, called do-search, is provably sound, and it is complete with respect to identifiability problems that have been shown to be completely characterized by do-calculus. When extended with additional rules, the search is capable of handling missing data problems as well. With the versatile search, we are able to approach new problems such as combined transportability and selection bias, or multiple sources of selection bias. We also perform a systematic analysis of bivariate missing data problems and study causal inference under case-control design.
Causal Discovery from Subsampled Time Series Data by Constraint Optimization
Jul 13, 2016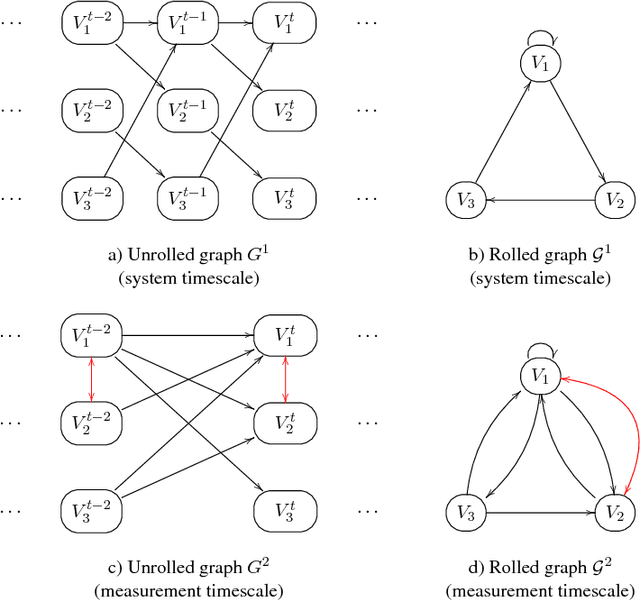
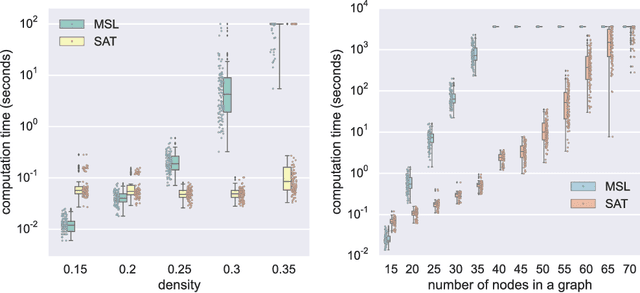
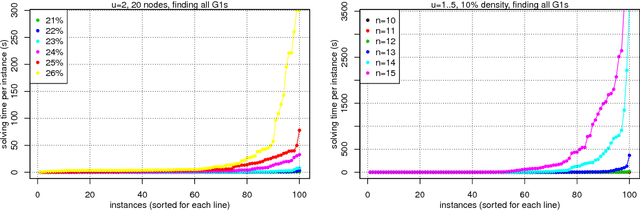
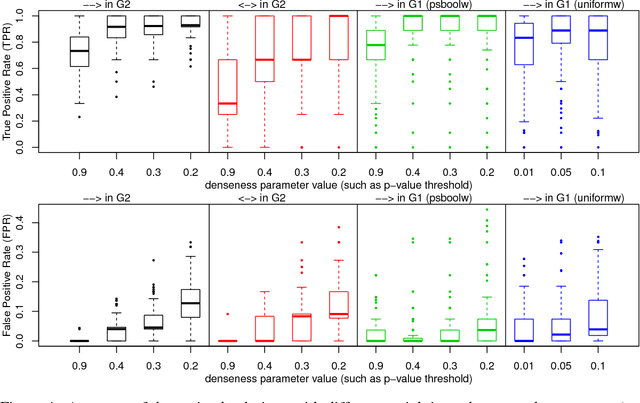
Abstract:This paper focuses on causal structure estimation from time series data in which measurements are obtained at a coarser timescale than the causal timescale of the underlying system. Previous work has shown that such subsampling can lead to significant errors about the system's causal structure if not properly taken into account. In this paper, we first consider the search for the system timescale causal structures that correspond to a given measurement timescale structure. We provide a constraint satisfaction procedure whose computational performance is several orders of magnitude better than previous approaches. We then consider finite-sample data as input, and propose the first constraint optimization approach for recovering the system timescale causal structure. This algorithm optimally recovers from possible conflicts due to statistical errors. More generally, these advances allow for a robust and non-parametric estimation of system timescale causal structures from subsampled time series data.
Discovering Cyclic Causal Models with Latent Variables: A General SAT-Based Procedure
Sep 26, 2013



Abstract:We present a very general approach to learning the structure of causal models based on d-separation constraints, obtained from any given set of overlapping passive observational or experimental data sets. The procedure allows for both directed cycles (feedback loops) and the presence of latent variables. Our approach is based on a logical representation of causal pathways, which permits the integration of quite general background knowledge, and inference is performed using a Boolean satisfiability (SAT) solver. The procedure is complete in that it exhausts the available information on whether any given edge can be determined to be present or absent, and returns "unknown" otherwise. Many existing constraint-based causal discovery algorithms can be seen as special cases, tailored to circumstances in which one or more restricting assumptions apply. Simulations illustrate the effect of these assumptions on discovery and how the present algorithm scales.
Causal Discovery of Linear Cyclic Models from Multiple Experimental Data Sets with Overlapping Variables
Oct 16, 2012



Abstract:Much of scientific data is collected as randomized experiments intervening on some and observing other variables of interest. Quite often, a given phenomenon is investigated in several studies, and different sets of variables are involved in each study. In this article we consider the problem of integrating such knowledge, inferring as much as possible concerning the underlying causal structure with respect to the union of observed variables from such experimental or passive observational overlapping data sets. We do not assume acyclicity or joint causal sufficiency of the underlying data generating model, but we do restrict the causal relationships to be linear and use only second order statistics of the data. We derive conditions for full model identifiability in the most generic case, and provide novel techniques for incorporating an assumption of faithfulness to aid in inference. In each case we seek to establish what is and what is not determined by the data at hand.
Bayesian Discovery of Linear Acyclic Causal Models
May 09, 2012



Abstract:Methods for automated discovery of causal relationships from non-interventional data have received much attention recently. A widely used and well understood model family is given by linear acyclic causal models (recursive structural equation models). For Gaussian data both constraint-based methods (Spirtes et al., 1993; Pearl, 2000) (which output a single equivalence class) and Bayesian score-based methods (Geiger and Heckerman, 1994) (which assign relative scores to the equivalence classes) are available. On the contrary, all current methods able to utilize non-Gaussianity in the data (Shimizu et al., 2006; Hoyer et al., 2008) always return only a single graph or a single equivalence class, and so are fundamentally unable to express the degree of certainty attached to that output. In this paper we develop a Bayesian score-based approach able to take advantage of non-Gaussianity when estimating linear acyclic causal models, and we empirically demonstrate that, at least on very modest size networks, its accuracy is as good as or better than existing methods. We provide a complete code package (in R) which implements all algorithms and performs all of the analysis provided in the paper, and hope that this will further the application of these methods to solving causal inference problems.
Noisy-OR Models with Latent Confounding
Feb 14, 2012



Abstract:Given a set of experiments in which varying subsets of observed variables are subject to intervention, we consider the problem of identifiability of causal models exhibiting latent confounding. While identifiability is trivial when each experiment intervenes on a large number of variables, the situation is more complicated when only one or a few variables are subject to intervention per experiment. For linear causal models with latent variables Hyttinen et al. (2010) gave precise conditions for when such data are sufficient to identify the full model. While their result cannot be extended to discrete-valued variables with arbitrary cause-effect relationships, we show that a similar result can be obtained for the class of causal models whose conditional probability distributions are restricted to a `noisy-OR' parameterization. We further show that identification is preserved under an extension of the model that allows for negative influences, and present learning algorithms that we test for accuracy, scalability and robustness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge