Simulating counterfactuals

Counterfactual inference considers a hypothetical intervention in a parallel world that shares some evidence with the factual world. If the evidence specifies a conditional distribution on a manifold, counterfactuals may be analytically intractable. We present an algorithm for simulating values from a counterfactual distribution where conditions can be set on both discrete and continuous variables. We show that the proposed algorithm can be presented as a particle filter leading to asymptotically valid inference. The algorithm is applied to fairness analysis in credit scoring.

Generalizing experimental findings: identification beyond adjustments

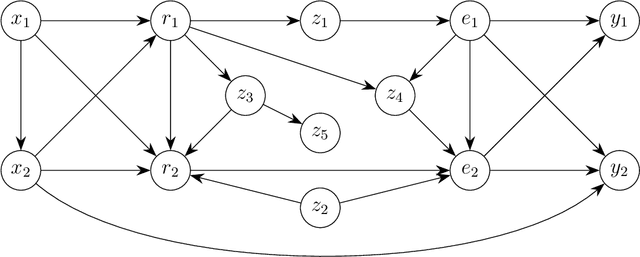
We aim to generalize the results of a randomized controlled trial (RCT) to a target population with the help of some observational data. This is a problem of causal effect identification with multiple data sources. Challenges arise when the RCT is conducted in a context that differs from the target population. Earlier research has focused on cases where the estimates from the RCT can be adjusted by observational data in order to remove the selection bias and other domain specific differences. We consider examples where the experimental findings cannot be generalized by an adjustment and show that the generalization may still be possible by other identification strategies that can be derived by applying do-calculus. The obtained identifying functionals for these examples contain trapdoor variables of a new type. The value of a trapdoor variable needs to be fixed in the estimation and the choice of the value may have a major effect on the bias and accuracy of estimates, which is also seen in simulations. The presented results expand the scope of settings where the generalization of experimental findings is doable

Clustering and Structural Robustness in Causal Diagrams

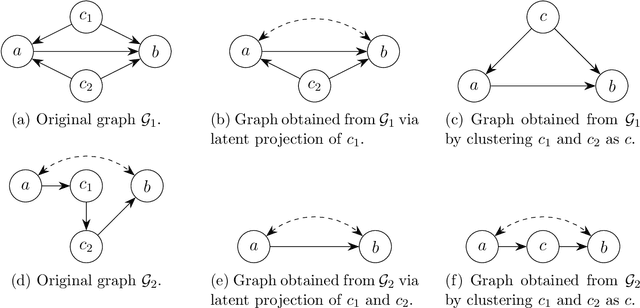
Graphs are commonly used to represent and visualize causal relations. For a small number of variables, this approach provides a succinct and clear view of the scenario at hand. As the number of variables under study increases, the graphical approach may become impractical, and the clarity of the representation is lost. Clustering of variables is a natural way to reduce the size of the causal diagram but it may erroneously change the essential properties of the causal relations if implemented arbitrarily. We define a specific type of cluster, called transit cluster, that is guaranteed to preserve the identifiability properties of causal effects under certain conditions. We provide a sound and complete algorithm for finding all transit clusters in a given graph and demonstrate how clustering can simplify the identification of causal effects. We also study the inverse problem, where one starts with a clustered graph and looks for extended graphs where the identifiability properties of causal effects remain unchanged. We show that this kind of structural robustness is closely related to transit clusters.

Identifying Causal Effects via Context-specific Independence Relations

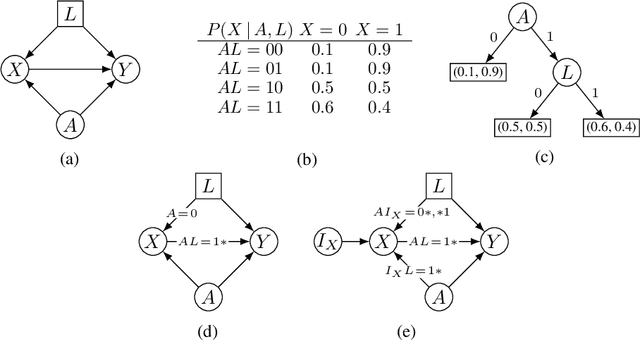
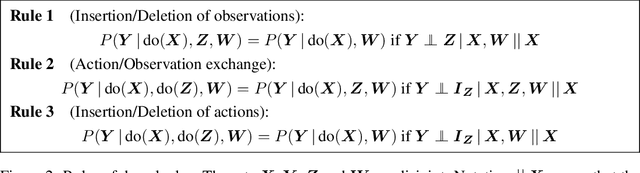
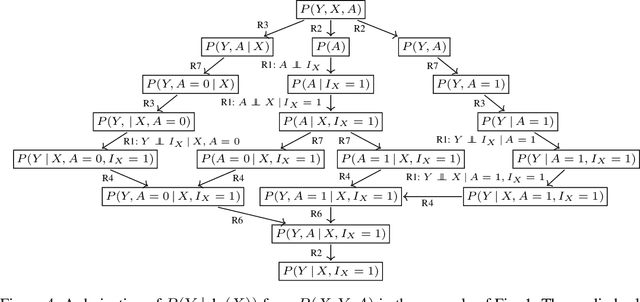
Causal effect identification considers whether an interventional probability distribution can be uniquely determined from a passively observed distribution in a given causal structure. If the generating system induces context-specific independence (CSI) relations, the existing identification procedures and criteria based on do-calculus are inherently incomplete. We show that deciding causal effect non-identifiability is NP-hard in the presence of CSIs. Motivated by this, we design a calculus and an automated search procedure for identifying causal effects in the presence of CSIs. The approach is provably sound and it includes standard do-calculus as a special case. With the approach we can obtain identifying formulas that were unobtainable previously, and demonstrate that a small number of CSI-relations may be sufficient to turn a previously non-identifiable instance to identifiable.

Causal Effect Identification from Multiple Incomplete Data Sources: A General Search-based Approach

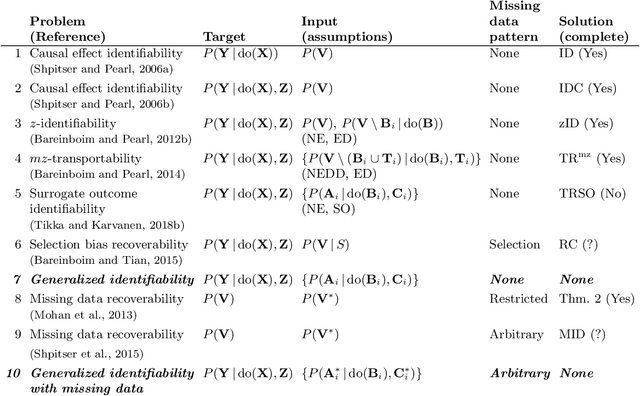
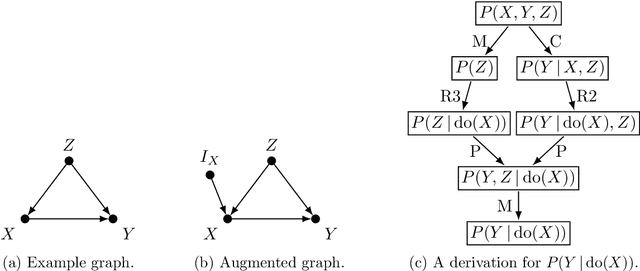
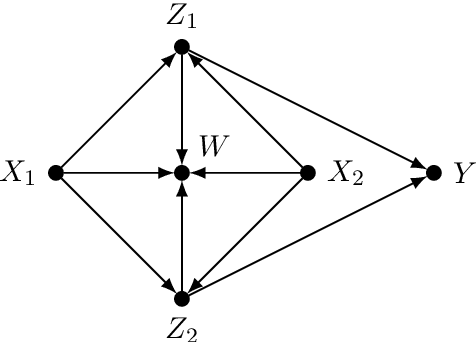
Causal effect identification considers whether an interventional probability distribution can be uniquely determined without parametric assumptions from measured source distributions and structural knowledge on the generating system. While complete graphical criteria and procedures exist for many identification problems, there are still challenging but important extensions that have not been considered in the literature. To tackle these new settings, we present a search algorithm directly over the rules of do-calculus. Due to generality of do-calculus, the search is capable of taking more advanced data-generating mechanisms into account along with an arbitrary type of both observational and experimental source distributions. The search is enhanced via a heuristic and search space reduction techniques. The approach, called do-search, is provably sound, and it is complete with respect to identifiability problems that have been shown to be completely characterized by do-calculus. When extended with additional rules, the search is capable of handling missing data problems as well. With the versatile search, we are able to approach new problems such as combined transportability and selection bias, or multiple sources of selection bias. We also perform a systematic analysis of bivariate missing data problems and study causal inference under case-control design.

Surrogate Outcomes and Transportability

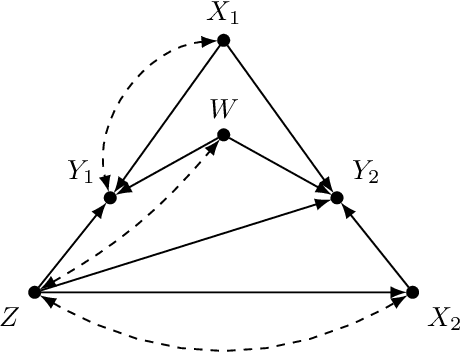
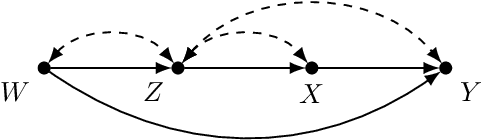
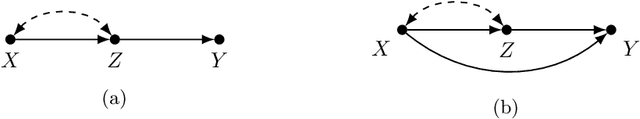
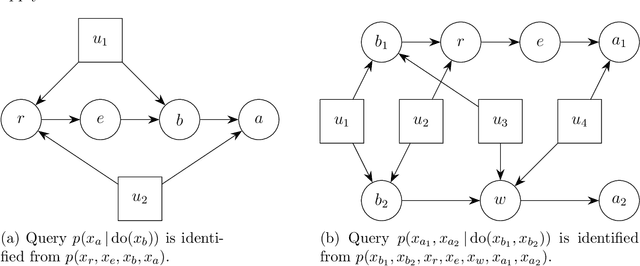
Identification of causal effects is one of the most fundamental tasks of causal inference. We consider a variant of the identifiability problem where a causal effect of interest is not identifiable from observational data alone but some experimental data is available for the identification task. This corresponds to a real-world setting where experiments were conducted on a set of variables, which we call surrogate outcomes, but the variables of interest were not measured. This problem is a generalization of identifiability using surrogate experiments and we label it as surrogate outcome identifiability and show that the concept of transportability provides a sufficient criteria for determining surrogate outcome identifiability for a large class of queries.

Enhancing Identification of Causal Effects by Pruning

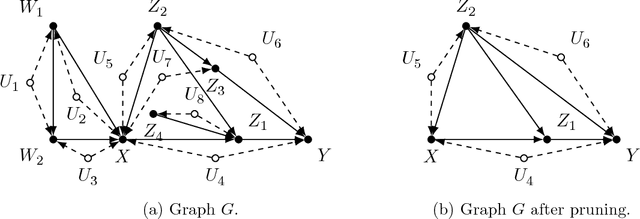
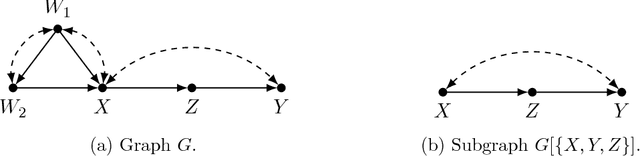
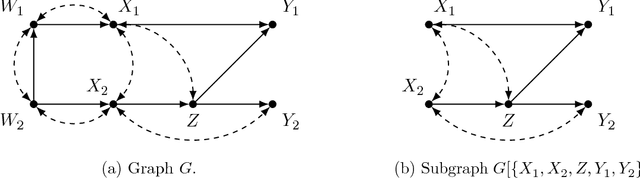
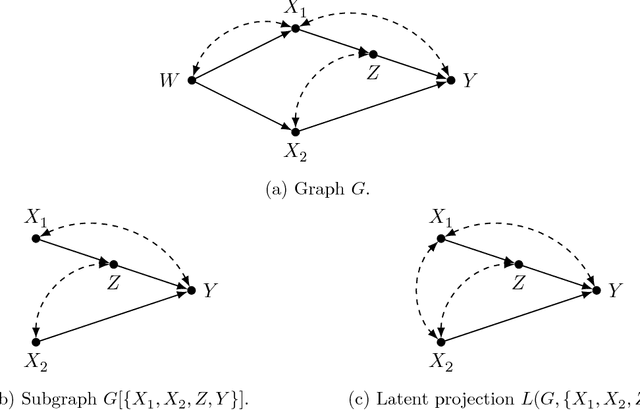
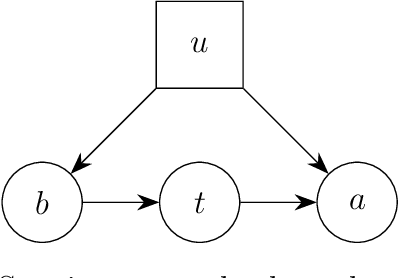
Causal models communicate our assumptions about causes and effects in real-world phe- nomena. Often the interest lies in the identification of the effect of an action which means deriving an expression from the observed probability distribution for the interventional distribution resulting from the action. In many cases an identifiability algorithm may return a complicated expression that contains variables that are in fact unnecessary. In practice this can lead to additional computational burden and increased bias or inefficiency of estimates when dealing with measurement error or missing data. We present graphical criteria to detect variables which are redundant in identifying causal effects. We also provide an improved version of a well-known identifiability algorithm that implements these criteria.

Simplifying Probabilistic Expressions in Causal Inference

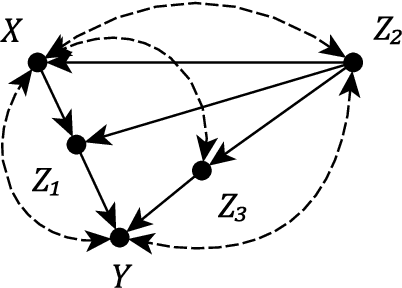
Obtaining a non-parametric expression for an interventional distribution is one of the most fundamental tasks in causal inference. Such an expression can be obtained for an identifiable causal effect by an algorithm or by manual application of do-calculus. Often we are left with a complicated expression which can lead to biased or inefficient estimates when missing data or measurement errors are involved. We present an automatic simplification algorithm that seeks to eliminate symbolically unnecessary variables from these expressions by taking advantage of the structure of the underlying graphical model. Our method is applicable to all causal effect formulas and is readily available in the R package causaleffect.

Estimating complex causal effects from incomplete observational data

Despite the major advances taken in causal modeling, causality is still an unfamiliar topic for many statisticians. In this paper, it is demonstrated from the beginning to the end how causal effects can be estimated from observational data assuming that the causal structure is known. To make the problem more challenging, the causal effects are highly nonlinear and the data are missing at random. The tools used in the estimation include causal models with design, causal calculus, multiple imputation and generalized additive models. The main message is that a trained statistician can estimate causal effects by judiciously combining existing tools.

Study design in causal models

The causal assumptions, the study design and the data are the elements required for scientific inference in empirical research. The research is adequately communicated only if all of these elements and their relations are described precisely. Causal models with design describe the study design and the missing data mechanism together with the causal structure and allow the direct application of causal calculus in the estimation of the causal effects. The flow of the study is visualized by ordering the nodes of the causal diagram in two dimensions by their causal order and the time of the observation. Conclusions whether a causal or observational relationship can be estimated from the collected incomplete data can be made directly from the graph. Causal models with design offer a systematic and unifying view scientific inference and increase the clarity and speed of communication. Examples on the causal models for a case-control study, a nested case-control study, a clinical trial and a two-stage case-cohort study are presented.