Jouni Helske
Clustering and Structural Robustness in Causal Diagrams
Nov 08, 2021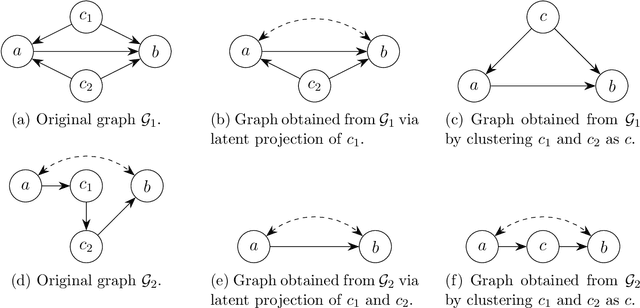
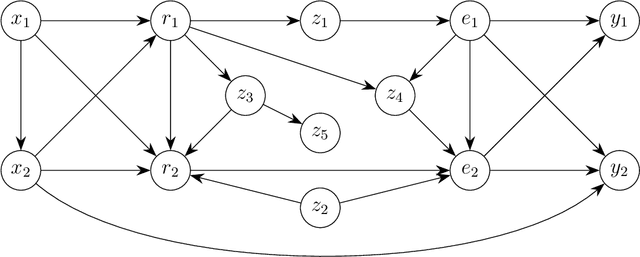
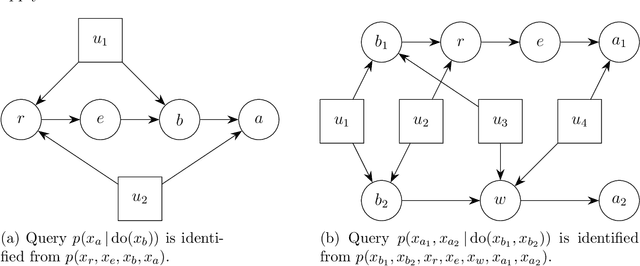
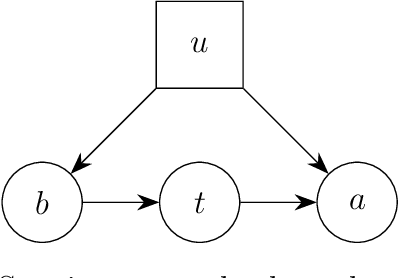
Abstract:Graphs are commonly used to represent and visualize causal relations. For a small number of variables, this approach provides a succinct and clear view of the scenario at hand. As the number of variables under study increases, the graphical approach may become impractical, and the clarity of the representation is lost. Clustering of variables is a natural way to reduce the size of the causal diagram but it may erroneously change the essential properties of the causal relations if implemented arbitrarily. We define a specific type of cluster, called transit cluster, that is guaranteed to preserve the identifiability properties of causal effects under certain conditions. We provide a sound and complete algorithm for finding all transit clusters in a given graph and demonstrate how clustering can simplify the identification of causal effects. We also study the inverse problem, where one starts with a clustered graph and looks for extended graphs where the identifiability properties of causal effects remain unchanged. We show that this kind of structural robustness is closely related to transit clusters.
Graphical model inference: Sequential Monte Carlo meets deterministic approximations
Jan 08, 2019


Abstract:Approximate inference in probabilistic graphical models (PGMs) can be grouped into deterministic methods and Monte-Carlo-based methods. The former can often provide accurate and rapid inferences, but are typically associated with biases that are hard to quantify. The latter enjoy asymptotic consistency, but can suffer from high computational costs. In this paper we present a way of bridging the gap between deterministic and stochastic inference. Specifically, we suggest an efficient sequential Monte Carlo (SMC) algorithm for PGMs which can leverage the output from deterministic inference methods. While generally applicable, we show explicitly how this can be done with loopy belief propagation, expectation propagation, and Laplace approximations. The resulting algorithm can be viewed as a post-correction of the biases associated with these methods and, indeed, numerical results show clear improvements over the baseline deterministic methods as well as over "plain" SMC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge