Simulating counterfactuals

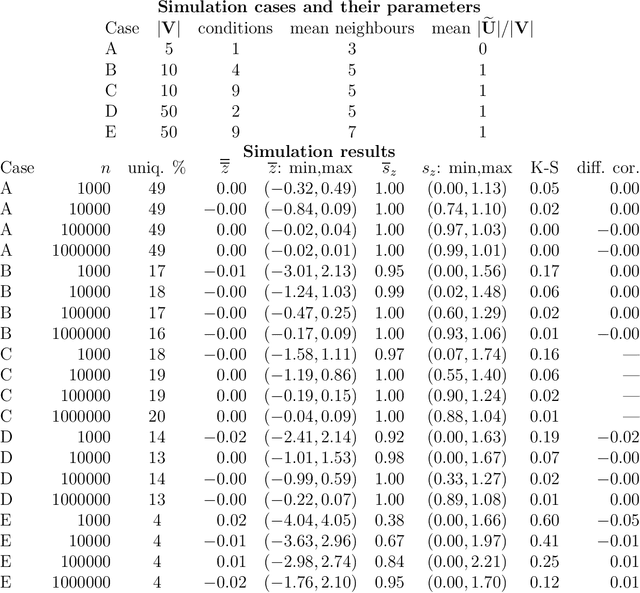
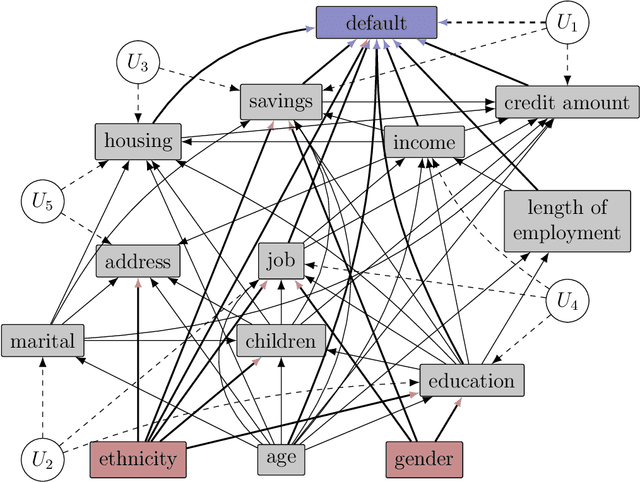
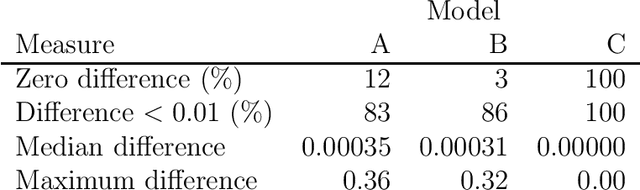
Counterfactual inference considers a hypothetical intervention in a parallel world that shares some evidence with the factual world. If the evidence specifies a conditional distribution on a manifold, counterfactuals may be analytically intractable. We present an algorithm for simulating values from a counterfactual distribution where conditions can be set on both discrete and continuous variables. We show that the proposed algorithm can be presented as a particle filter leading to asymptotically valid inference. The algorithm is applied to fairness analysis in credit scoring.