Identifiability of Discretized Latent Coordinate Systems via Density Landmarks Detection

Disentanglement aims to recover meaningful latent ground-truth factors from only the observed distribution. Identifiability provides the theoretical grounding for disentanglement to be well-founded. Unfortunately, unsupervised identifiability of independent latent factors is a theoretically proven impossibility in the i.i.d. setting under a general nonlinear smooth map from factors to observations. In this work, we show that, remarkably, it is possible to recover discretized latent coordinates under a highly generic nonlinear smooth mapping (a diffeomorphism) without any additional inductive bias on the mapping. This is, assuming that latent density has axis-aligned discontinuity landmarks, but without making the unrealistic assumption of statistical independence of the factors. We introduce this novel form of identifiability, termed quantized coordinate identifiability, and provide a comprehensive proof of the recovery of discretized coordinates.

Binary Independent Component Analysis via Non-stationarity

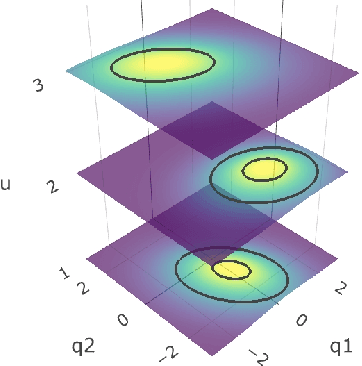
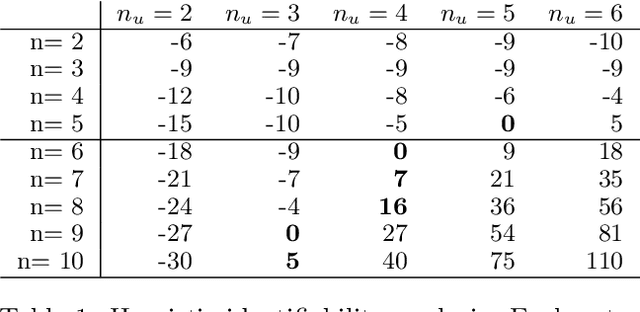
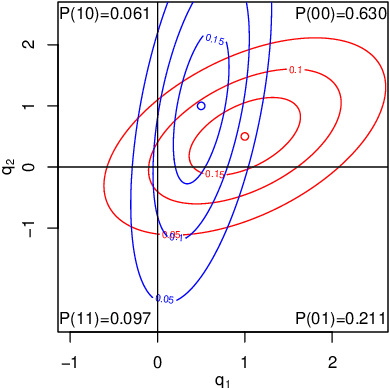
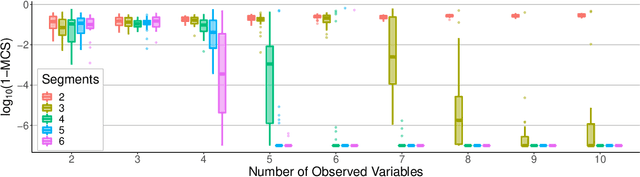
We consider independent component analysis of binary data. While fundamental in practice, this case has been much less developed than ICA for continuous data. We start by assuming a linear mixing model in a continuous-valued latent space, followed by a binary observation model. Importantly, we assume that the sources are non-stationary; this is necessary since any non-Gaussianity would essentially be destroyed by the binarization. Interestingly, the model allows for closed-form likelihood by employing the cumulative distribution function of the multivariate Gaussian distribution. In stark contrast to the continuous-valued case, we prove non-identifiability of the model with few observed variables; our empirical results imply identifiability when the number of observed variables is higher. We present a practical method for binary ICA that uses only pairwise marginals, which are faster to compute than the full multivariate likelihood.