Efficient and Reliable Hitting-Set Computations for the Implicit Hitting Set Approach

The implicit hitting set (IHS) approach offers a general framework for solving computationally hard combinatorial optimization problems declaratively. IHS iterates between a decision oracle used for extracting sources of inconsistency and an optimizer for computing so-called hitting sets (HSs) over the accumulated sources of inconsistency. While the decision oracle is language-specific, the optimizers is usually instantiated through integer programming. We explore alternative algorithmic techniques for hitting set optimization based on different ways of employing pseudo-Boolean (PB) reasoning as well as stochastic local search. We extensively evaluate the practical feasibility of the alternatives in particular in the context of pseudo-Boolean (0-1 IP) optimization as one of the most recent instantiations of IHS. Highlighting a trade-off between efficiency and reliability, while a commercial IP solver turns out to remain the most effective way to instantiate HS computations, it can cause correctness issues due to numerical instability; in fact, we show that exact HS computations instantiated via PB reasoning can be made competitive with a numerically exact IP solver. Furthermore, the use of PB reasoning as a basis for HS computations allows for obtaining certificates for the correctness of IHS computations, generally applicable to any IHS instantiation in which reasoning in the declarative language at hand can be captured in the PB-based proof format we employ.

Symmetry breaking for inductive logic programming

The goal of inductive logic programming is to search for a hypothesis that generalises training data and background knowledge. The challenge is searching vast hypothesis spaces, which is exacerbated because many logically equivalent hypotheses exist. To address this challenge, we introduce a method to break symmetries in the hypothesis space. We implement our idea in answer set programming. Our experiments on multiple domains, including visual reasoning and game playing, show that our approach can reduce solving times from over an hour to just 17 seconds.

Certifying Pareto-Optimality in Multi-Objective Maximum Satisfiability

Due to the wide employment of automated reasoning in the analysis and construction of correct systems, the results reported by automated reasoning engines must be trustworthy. For Boolean satisfiability (SAT) solvers - and more recently SAT-based maximum satisfiability (MaxSAT) solvers - trustworthiness is obtained by integrating proof logging into solvers, making solvers capable of emitting machine-verifiable proofs to certify correctness of the reasoning steps performed. In this work, we enable for the first time proof logging based on the VeriPB proof format for multi-objective MaxSAT (MO-MaxSAT) optimization techniques. Although VeriPB does not offer direct support for multi-objective problems, we detail how preorders in VeriPB can be used to provide certificates for MO-MaxSAT algorithms computing a representative solution for each element in the non-dominated set of the search space under Pareto-optimality, without extending the VeriPB format or the proof checker. By implementing VeriPB proof logging into a state-of-the-art multi-objective MaxSAT solver, we show empirically that proof logging can be made scalable for MO-MaxSAT with reasonable overhead.

Certified MaxSAT Preprocessing

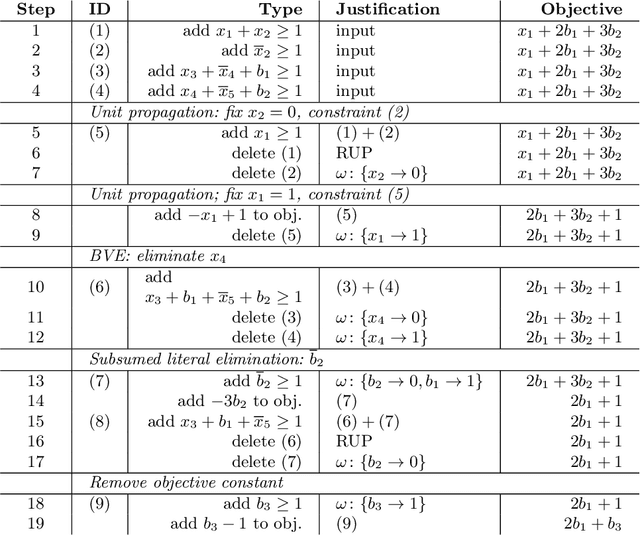
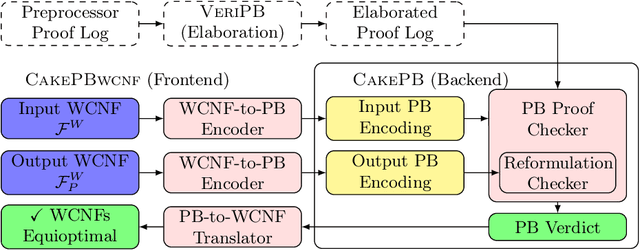
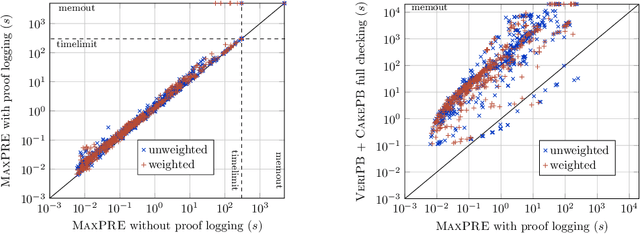
Building on the progress in Boolean satisfiability (SAT) solving over the last decades, maximum satisfiability (MaxSAT) has become a viable approach for solving NP-hard optimization problems, but ensuring correctness of MaxSAT solvers has remained an important concern. For SAT, this is largely a solved problem thanks to the use of proof logging, meaning that solvers emit machine-verifiable proofs of (un)satisfiability to certify correctness. However, for MaxSAT, proof logging solvers have started being developed only very recently. Moreover, these nascent efforts have only targeted the core solving process, ignoring the preprocessing phase where input problem instances can be substantially reformulated before being passed on to the solver proper. In this work, we demonstrate how pseudo-Boolean proof logging can be used to certify the correctness of a wide range of modern MaxSAT preprocessing techniques. By combining and extending the VeriPB and CakePB tools, we provide formally verified, end-to-end proof checking that the input and preprocessed output MaxSAT problem instances have the same optimal value. An extensive evaluation on applied MaxSAT benchmarks shows that our approach is feasible in practice.

Learning big logical rules by joining small rules

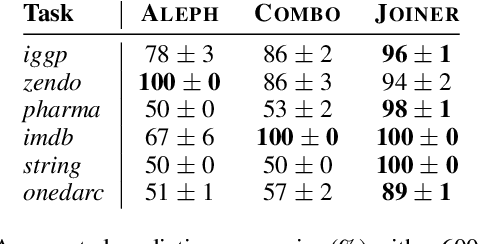
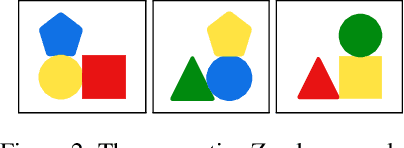
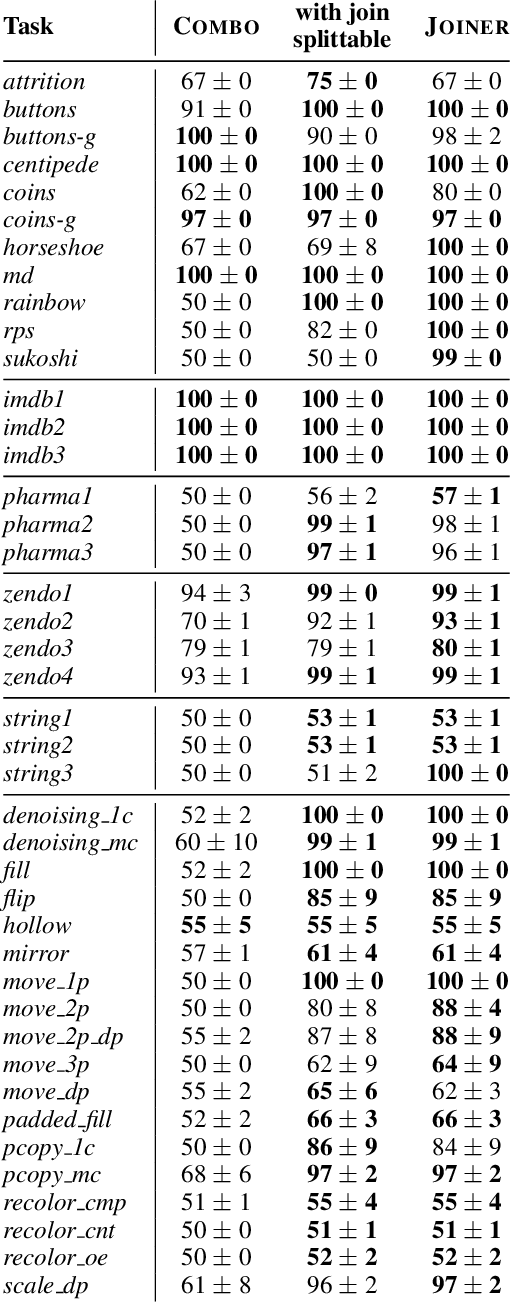
A major challenge in inductive logic programming is learning big rules. To address this challenge, we introduce an approach where we join small rules to learn big rules. We implement our approach in a constraint-driven system and use constraint solvers to efficiently join rules. Our experiments on many domains, including game playing and drug design, show that our approach can (i) learn rules with more than 100 literals, and (ii) drastically outperform existing approaches in terms of predictive accuracies.

SharpSAT-TD in Model Counting Competitions 2021-2023

We describe SharpSAT-TD, our submission to the unweighted and weighted tracks of the Model Counting Competition in 2021-2023, which has won in total $6$ first places in different tracks of the competition. SharpSAT-TD is based on SharpSAT [Thurley, SAT 2006], with the primary novel modification being the use of tree decompositions in the variable selection heuristic as introduced by the authors in [CP 2021]. Unlike the version of SharpSAT-TD evaluated in [CP 2021], the current version that is available in https://github.com/Laakeri/sharpsat-td features also other significant modifications compared to the original SharpSAT, for example, a new preprocessor.

Learning MDL logic programs from noisy data

Many inductive logic programming approaches struggle to learn programs from noisy data. To overcome this limitation, we introduce an approach that learns minimal description length programs from noisy data, including recursive programs. Our experiments on several domains, including drug design, game playing, and program synthesis, show that our approach can outperform existing approaches in terms of predictive accuracies and scale to moderate amounts of noise.

Harnessing Incremental Answer Set Solving for Reasoning in Assumption-Based Argumentation

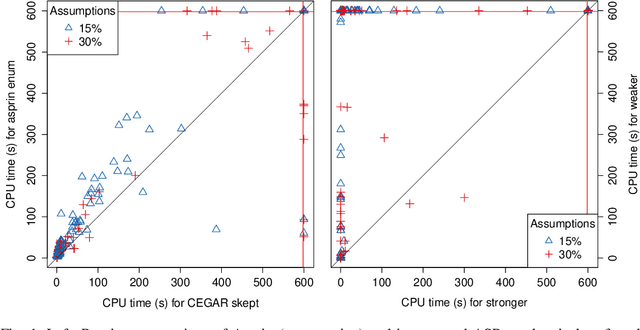
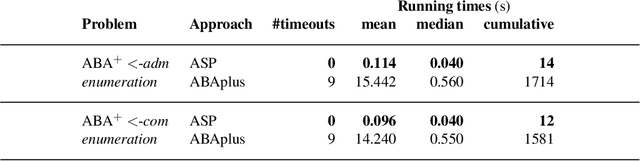
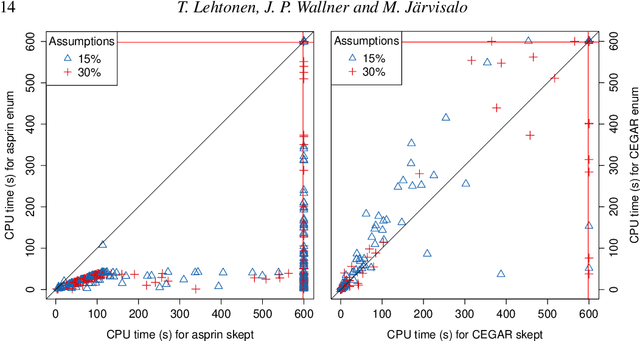
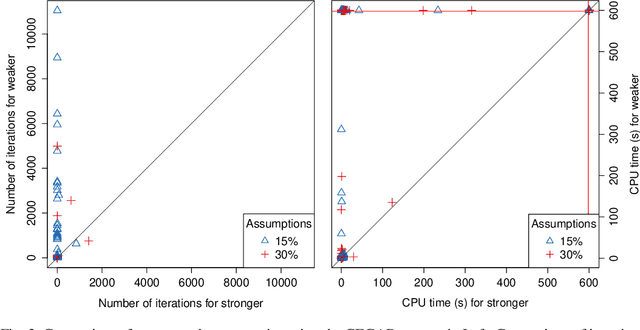
Assumption-based argumentation (ABA) is a central structured argumentation formalism. As shown recently, answer set programming (ASP) enables efficiently solving NP-hard reasoning tasks of ABA in practice, in particular in the commonly studied logic programming fragment of ABA. In this work, we harness recent advances in incremental ASP solving for developing effective algorithms for reasoning tasks in the logic programming fragment of ABA that are presumably hard for the second level of the polynomial hierarchy, including skeptical reasoning under preferred semantics as well as preferential reasoning. In particular, we develop non-trivial counterexample-guided abstraction refinement procedures based on incremental ASP solving for these tasks. We also show empirically that the procedures are significantly more effective than previously proposed algorithms for the tasks. This paper is under consideration for acceptance in TPLP.

Bayesian Network Structure Learning with Integer Programming: Polytopes, Facets, and Complexity

The challenging task of learning structures of probabilistic graphical models is an important problem within modern AI research. Recent years have witnessed several major algorithmic advances in structure learning for Bayesian networks---arguably the most central class of graphical models---especially in what is known as the score-based setting. A successful generic approach to optimal Bayesian network structure learning (BNSL), based on integer programming (IP), is implemented in the GOBNILP system. Despite the recent algorithmic advances, current understanding of foundational aspects underlying the IP based approach to BNSL is still somewhat lacking. Understanding fundamental aspects of cutting planes and the related separation problem( is important not only from a purely theoretical perspective, but also since it holds out the promise of further improving the efficiency of state-of-the-art approaches to solving BNSL exactly. In this paper, we make several theoretical contributions towards these goals: (i) we study the computational complexity of the separation problem, proving that the problem is NP-hard; (ii) we formalise and analyse the relationship between three key polytopes underlying the IP-based approach to BNSL; (iii) we study the facets of the three polytopes both from the theoretical and practical perspective, providing, via exhaustive computation, a complete enumeration of facets for low-dimensional family-variable polytopes; and, furthermore, (iv) we establish a tight connection of the BNSL problem to the acyclic subgraph problem.

Causal Discovery from Subsampled Time Series Data by Constraint Optimization

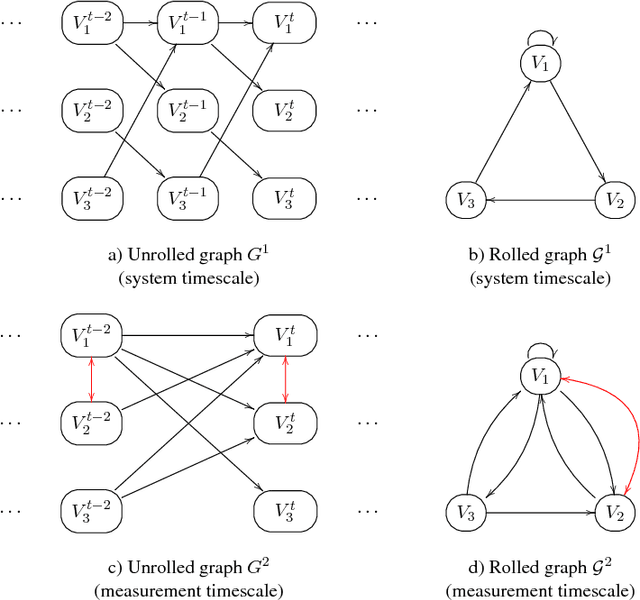
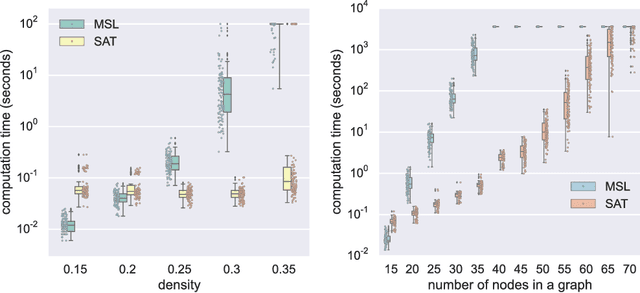
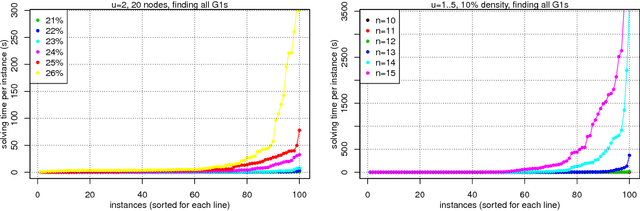
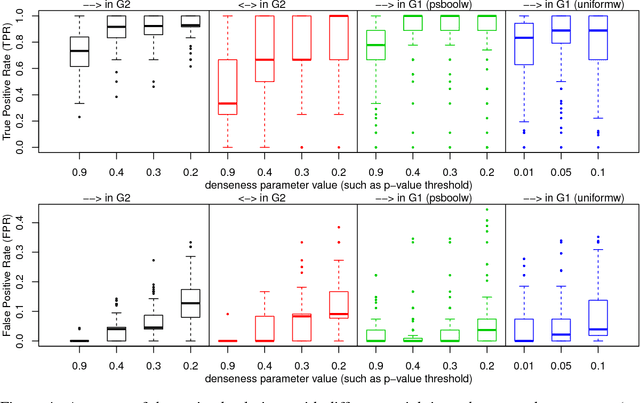
This paper focuses on causal structure estimation from time series data in which measurements are obtained at a coarser timescale than the causal timescale of the underlying system. Previous work has shown that such subsampling can lead to significant errors about the system's causal structure if not properly taken into account. In this paper, we first consider the search for the system timescale causal structures that correspond to a given measurement timescale structure. We provide a constraint satisfaction procedure whose computational performance is several orders of magnitude better than previous approaches. We then consider finite-sample data as input, and propose the first constraint optimization approach for recovering the system timescale causal structure. This algorithm optimally recovers from possible conflicts due to statistical errors. More generally, these advances allow for a robust and non-parametric estimation of system timescale causal structures from subsampled time series data.