A Score-and-Search Approach to Learning Bayesian Networks with Noisy-OR Relations

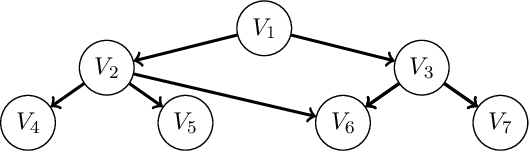
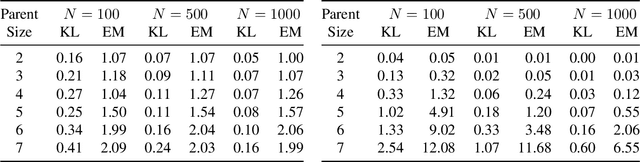
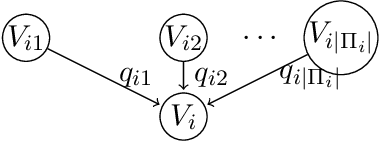
A Bayesian network is a probabilistic graphical model that consists of a directed acyclic graph (DAG), where each node is a random variable and attached to each node is a conditional probability distribution (CPD). A Bayesian network can be learned from data using the well-known score-and-search approach, and within this approach a key consideration is how to simultaneously learn the global structure in the form of the underlying DAG and the local structure in the CPDs. Several useful forms of local structure have been identified in the literature but thus far the score-and-search approach has only been extended to handle local structure in form of context-specific independence. In this paper, we show how to extend the score-and-search approach to the important and widely useful case of noisy-OR relations. We provide an effective gradient descent algorithm to score a candidate noisy-OR using the widely used BIC score and we provide pruning rules that allow the search to successfully scale to medium sized networks. Our empirical results provide evidence for the success of our approach to learning Bayesian networks that incorporate noisy-OR relations.

Learning All Credible Bayesian Network Structures for Model Averaging

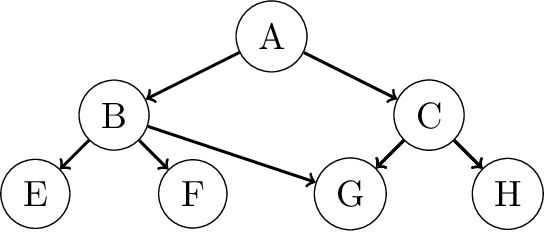
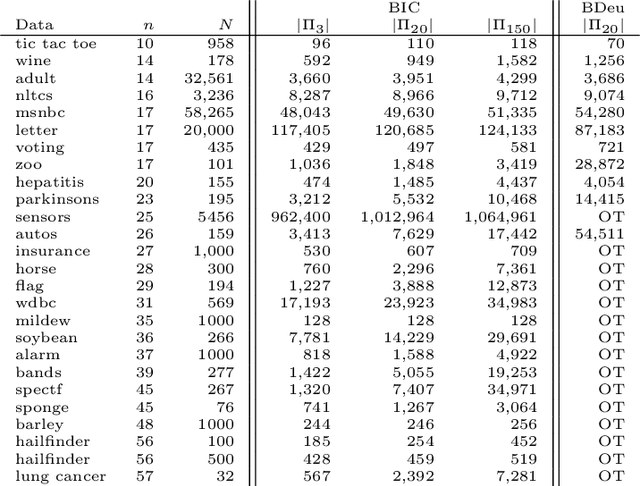
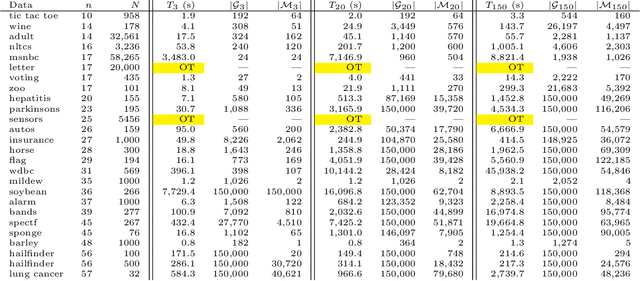
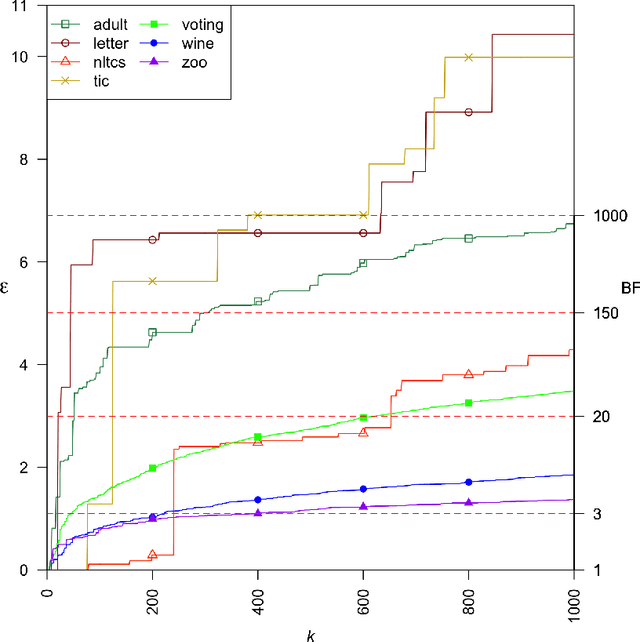
A Bayesian network is a widely used probabilistic graphical model with applications in knowledge discovery and prediction. Learning a Bayesian network (BN) from data can be cast as an optimization problem using the well-known score-and-search approach. However, selecting a single model (i.e., the best scoring BN) can be misleading or may not achieve the best possible accuracy. An alternative to committing to a single model is to perform some form of Bayesian or frequentist model averaging, where the space of possible BNs is sampled or enumerated in some fashion. Unfortunately, existing approaches for model averaging either severely restrict the structure of the Bayesian network or have only been shown to scale to networks with fewer than 30 random variables. In this paper, we propose a novel approach to model averaging inspired by performance guarantees in approximation algorithms. Our approach has two primary advantages. First, our approach only considers credible models in that they are optimal or near-optimal in score. Second, our approach is more efficient and scales to significantly larger Bayesian networks than existing approaches.

Kernel-based Approach to Handle Mixed Data for Inferring Causal Graphs

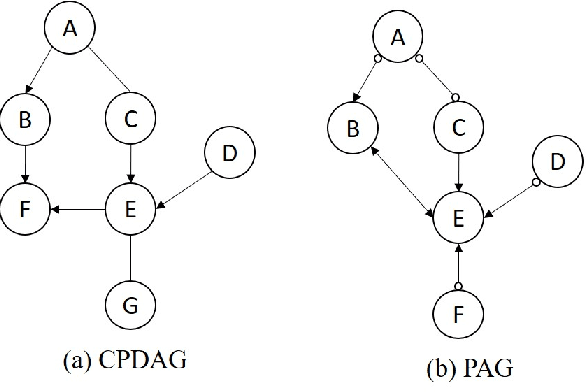
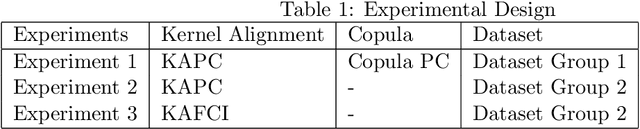
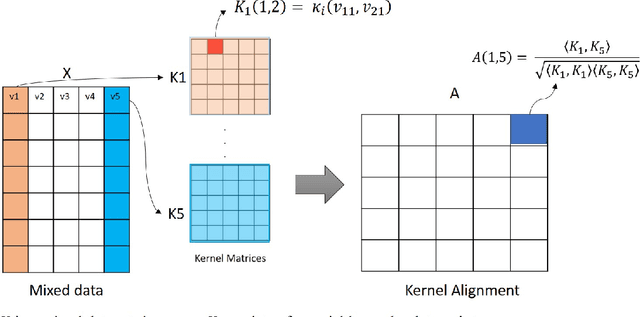
Causal learning is a beneficial approach to analyze the cause and effect relationships among variables in a dataset. A causal graph can be generated from a dataset using a particular causal algorithm, for instance, the PC algorithm or Fast Causal Inference (FCI). Generating a causal graph from a dataset that contains different data types (mixed data) is not trivial. This research offers an easy way to handle the mixed data so that it can be used to learn causal graphs using the existing application of the PC algorithm and FCI. This research proposes using kernel functions and Kernel Alignment to handle mixed data. Two main steps of this approach are computing a kernel matrix for each variable and calculating a pseudo-correlation matrix using Kernel Alignment. Kernel Alignment is used as a substitute for the correlation matrix for the conditional independence test for Gaussian data in the PC Algorithm and FCI. The advantage of this idea is that is possible to handle any data type by using a suitable kernel function to compute a kernel matrix for an observed variable. The proposed method is successfully applied to learn a causal graph from mixed data containing categorical, binary, ordinal, and continuous variables.

On Pruning for Score-Based Bayesian Network Structure Learning

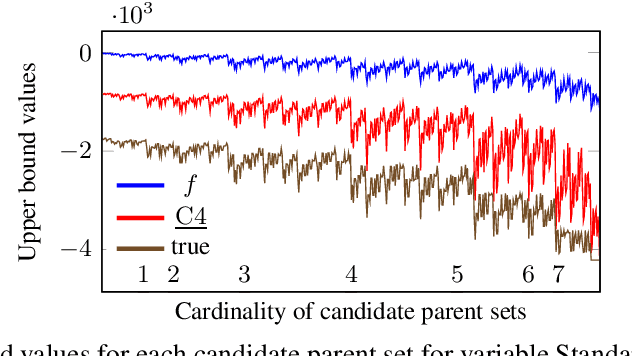
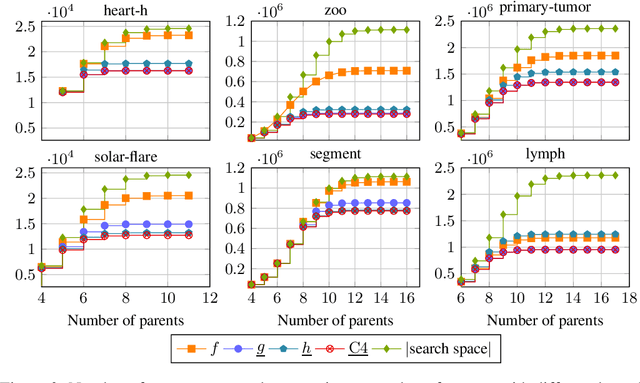
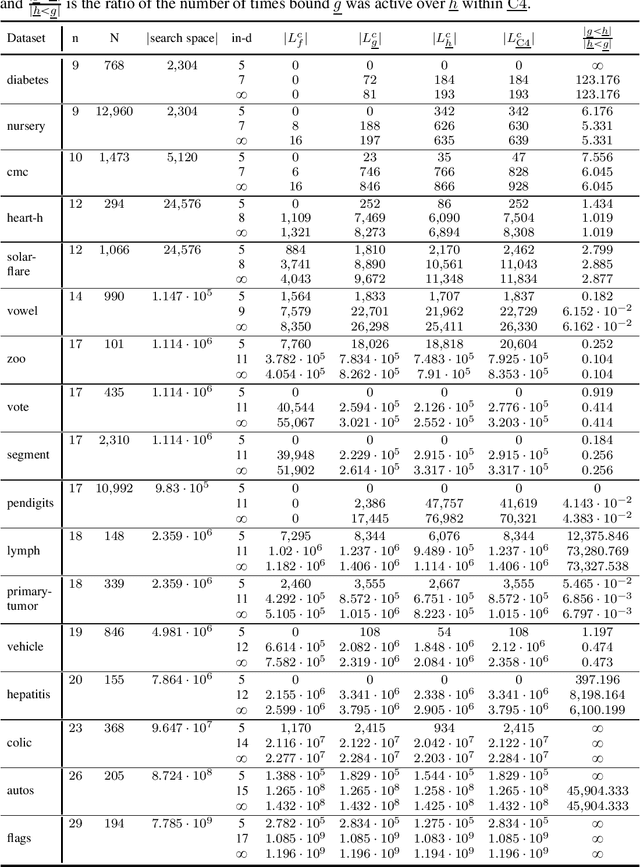
Many algorithms for score-based Bayesian network structure learning (BNSL) take as input a collection of potentially optimal parent sets for each variable in a data set. Constructing these collections naively is computationally intensive since the number of parent sets grows exponentially with the number of variables. Therefore, pruning techniques are not only desirable but essential. While effective pruning exists for the Bayesian Information Criterion (BIC), current results for the Bayesian Dirichlet equivalent uniform (BDeu) score reduce the search space very modestly, hampering the use of (the often preferred) BDeu. We derive new non-trivial theoretical upper bounds for the BDeu score that considerably improve on the state of the art. Since the new bounds are efficient and easy to implement, they can be promptly integrated into many BNSL methods. We show that gains can be significant in multiple UCI data sets so as to highlight practical implications of the theoretical advances.

Online Causal Structure Learning in the Presence of Latent Variables

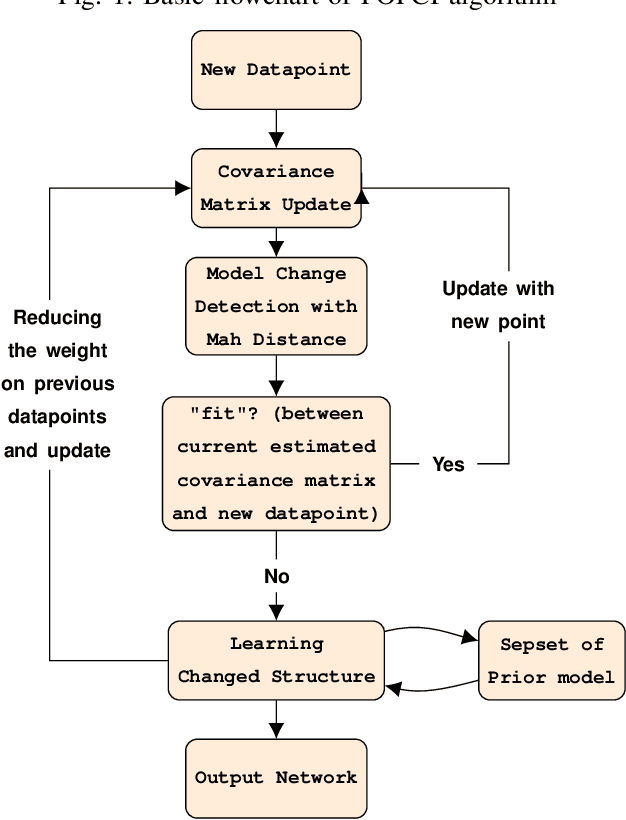
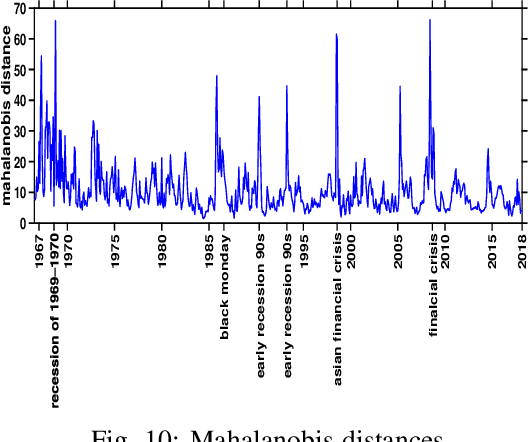
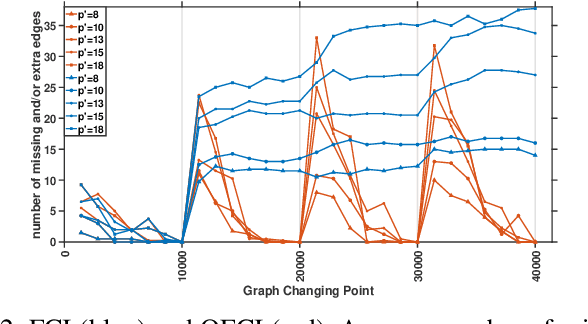
We present two online causal structure learning algorithms which can track changes in a causal structure and process data in a dynamic real-time manner. Standard causal structure learning algorithms assume that causal structure does not change during the data collection process, but in real-world scenarios, it does often change. Therefore, it is inappropriate to handle such changes with existing batch-learning approaches, and instead, a structure should be learned in an online manner. The online causal structure learning algorithms we present here can revise correlation values without reprocessing the entire dataset and use an existing model to avoid relearning the causal links in the prior model, which still fit data. Proposed algorithms are tested on synthetic and real-world datasets, the latter being a seasonally adjusted commodity price index dataset for the U.S. The online causal structure learning algorithms outperformed standard FCI by a large margin in learning the changed causal structure correctly and efficiently when latent variables were present.

Finding All Bayesian Network Structures within a Factor of Optimal

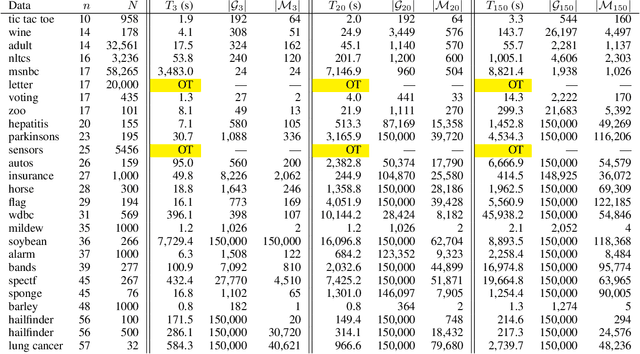
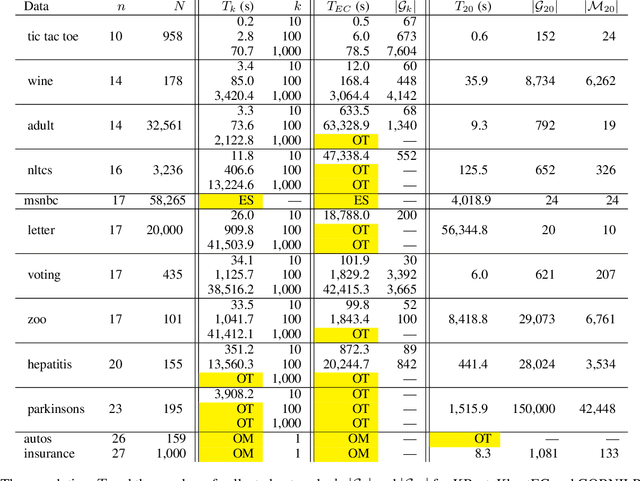
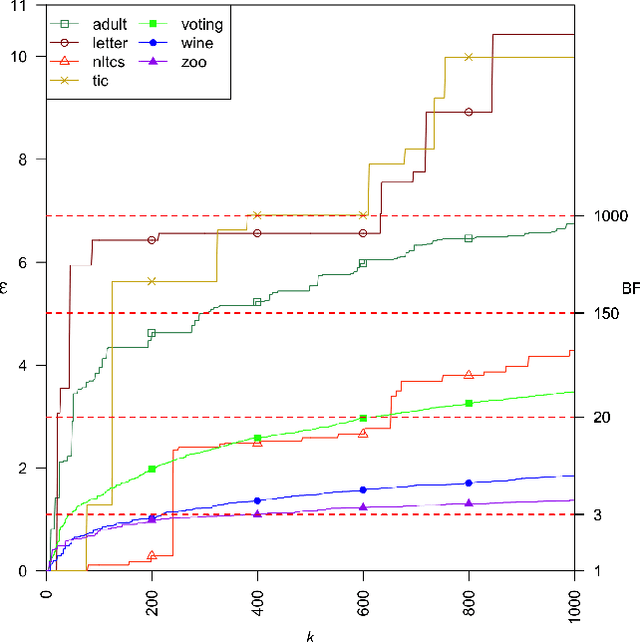
A Bayesian network is a widely used probabilistic graphical model with applications in knowledge discovery and prediction. Learning a Bayesian network (BN) from data can be cast as an optimization problem using the well-known score-and-search approach. However, selecting a single model (i.e., the best scoring BN) can be misleading or may not achieve the best possible accuracy. An alternative to committing to a single model is to perform some form of Bayesian or frequentist model averaging, where the space of possible BNs is sampled or enumerated in some fashion. Unfortunately, existing approaches for model averaging either severely restrict the structure of the Bayesian network or have only been shown to scale to networks with fewer than 30 random variables. In this paper, we propose a novel approach to model averaging inspired by performance guarantees in approximation algorithms. Our approach has two primary advantages. First, our approach only considers credible models in that they are optimal or near-optimal in score. Second, our approach is more efficient and scales to significantly larger Bayesian networks than existing approaches.

Finding Minimal Cost Herbrand Models with Branch-Cut-and-Price

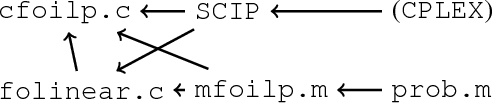
Given (1) a set of clauses $T$ in some first-order language $\cal L$ and (2) a cost function $c : B_{{\cal L}} \rightarrow \mathbb{R}_{+}$, mapping each ground atom in the Herbrand base $B_{{\cal L}}$ to a non-negative real, then the problem of finding a minimal cost Herbrand model is to either find a Herbrand model $\cal I$ of $T$ which is guaranteed to minimise the sum of the costs of true ground atoms, or establish that there is no Herbrand model for $T$. A branch-cut-and-price integer programming (IP) approach to solving this problem is presented. Since the number of ground instantiations of clauses and the size of the Herbrand base are both infinite in general, we add the corresponding IP constraints and IP variables `on the fly' via `cutting' and `pricing' respectively. In the special case of a finite Herbrand base we show that adding all IP variables and constraints from the outset can be advantageous, showing that a challenging Markov logic network MAP problem can be solved in this way if encoded appropriately.

Bayesian Network Structure Learning with Integer Programming: Polytopes, Facets, and Complexity

The challenging task of learning structures of probabilistic graphical models is an important problem within modern AI research. Recent years have witnessed several major algorithmic advances in structure learning for Bayesian networks---arguably the most central class of graphical models---especially in what is known as the score-based setting. A successful generic approach to optimal Bayesian network structure learning (BNSL), based on integer programming (IP), is implemented in the GOBNILP system. Despite the recent algorithmic advances, current understanding of foundational aspects underlying the IP based approach to BNSL is still somewhat lacking. Understanding fundamental aspects of cutting planes and the related separation problem( is important not only from a purely theoretical perspective, but also since it holds out the promise of further improving the efficiency of state-of-the-art approaches to solving BNSL exactly. In this paper, we make several theoretical contributions towards these goals: (i) we study the computational complexity of the separation problem, proving that the problem is NP-hard; (ii) we formalise and analyse the relationship between three key polytopes underlying the IP-based approach to BNSL; (iii) we study the facets of the three polytopes both from the theoretical and practical perspective, providing, via exhaustive computation, a complete enumeration of facets for low-dimensional family-variable polytopes; and, furthermore, (iv) we establish a tight connection of the BNSL problem to the acyclic subgraph problem.

First-order integer programming for MAP problems

Finding the most probable (MAP) model in SRL frameworks such as Markov logic and Problog can, in principle, be solved by encoding the problem as a `grounded-out' mixed integer program (MIP). However, useful first-order structure disappears in this process motivating the development of first-order MIP approaches. Here we present mfoilp, one such approach. Since the syntax and semantics of mfoilp is essentially the same as existing approaches we focus here mainly on implementation and algorithmic issues. We start with the (conceptually) simple problem of using a logic program to generate a MIP instance before considering more ambitious exploitation of first-order representations.

Advances in Bayesian Network Learning using Integer Programming

We consider the problem of learning Bayesian networks (BNs) from complete discrete data. This problem of discrete optimisation is formulated as an integer program (IP). We describe the various steps we have taken to allow efficient solving of this IP. These are (i) efficient search for cutting planes, (ii) a fast greedy algorithm to find high-scoring (perhaps not optimal) BNs and (iii) tightening the linear relaxation of the IP. After relating this BN learning problem to set covering and the multidimensional 0-1 knapsack problem, we present our empirical results. These show improvements, sometimes dramatic, over earlier results.