A Score-and-Search Approach to Learning Bayesian Networks with Noisy-OR Relations
Paper and Code
Nov 03, 2020
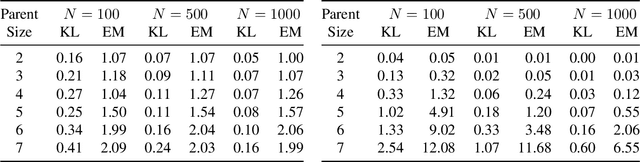
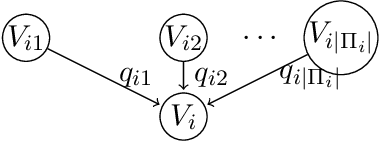

A Bayesian network is a probabilistic graphical model that consists of a directed acyclic graph (DAG), where each node is a random variable and attached to each node is a conditional probability distribution (CPD). A Bayesian network can be learned from data using the well-known score-and-search approach, and within this approach a key consideration is how to simultaneously learn the global structure in the form of the underlying DAG and the local structure in the CPDs. Several useful forms of local structure have been identified in the literature but thus far the score-and-search approach has only been extended to handle local structure in form of context-specific independence. In this paper, we show how to extend the score-and-search approach to the important and widely useful case of noisy-OR relations. We provide an effective gradient descent algorithm to score a candidate noisy-OR using the widely used BIC score and we provide pruning rules that allow the search to successfully scale to medium sized networks. Our empirical results provide evidence for the success of our approach to learning Bayesian networks that incorporate noisy-OR relations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge