A Score-and-Search Approach to Learning Bayesian Networks with Noisy-OR Relations

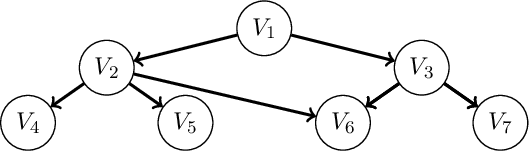
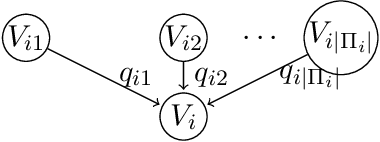
A Bayesian network is a probabilistic graphical model that consists of a directed acyclic graph (DAG), where each node is a random variable and attached to each node is a conditional probability distribution (CPD). A Bayesian network can be learned from data using the well-known score-and-search approach, and within this approach a key consideration is how to simultaneously learn the global structure in the form of the underlying DAG and the local structure in the CPDs. Several useful forms of local structure have been identified in the literature but thus far the score-and-search approach has only been extended to handle local structure in form of context-specific independence. In this paper, we show how to extend the score-and-search approach to the important and widely useful case of noisy-OR relations. We provide an effective gradient descent algorithm to score a candidate noisy-OR using the widely used BIC score and we provide pruning rules that allow the search to successfully scale to medium sized networks. Our empirical results provide evidence for the success of our approach to learning Bayesian networks that incorporate noisy-OR relations.

Learning All Credible Bayesian Network Structures for Model Averaging

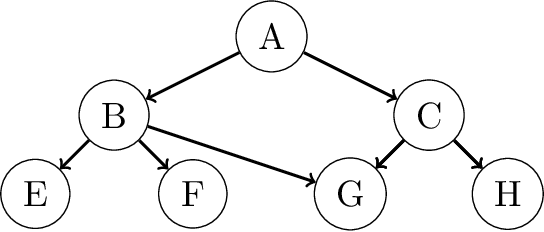
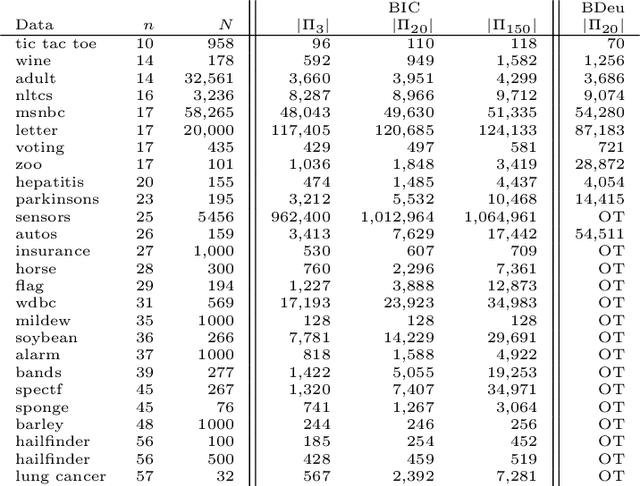
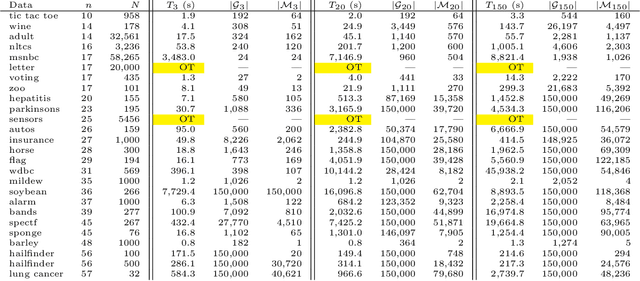
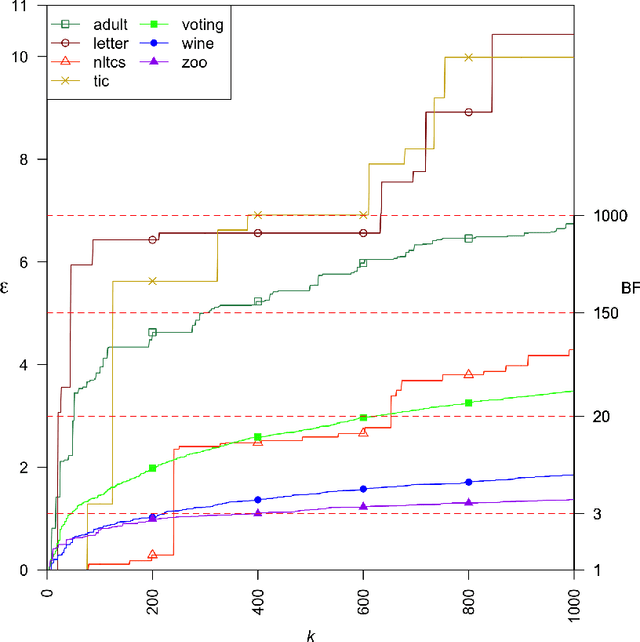
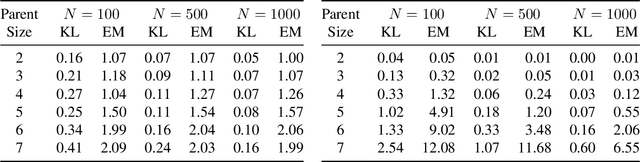
A Bayesian network is a widely used probabilistic graphical model with applications in knowledge discovery and prediction. Learning a Bayesian network (BN) from data can be cast as an optimization problem using the well-known score-and-search approach. However, selecting a single model (i.e., the best scoring BN) can be misleading or may not achieve the best possible accuracy. An alternative to committing to a single model is to perform some form of Bayesian or frequentist model averaging, where the space of possible BNs is sampled or enumerated in some fashion. Unfortunately, existing approaches for model averaging either severely restrict the structure of the Bayesian network or have only been shown to scale to networks with fewer than 30 random variables. In this paper, we propose a novel approach to model averaging inspired by performance guarantees in approximation algorithms. Our approach has two primary advantages. First, our approach only considers credible models in that they are optimal or near-optimal in score. Second, our approach is more efficient and scales to significantly larger Bayesian networks than existing approaches.

Finding All Bayesian Network Structures within a Factor of Optimal

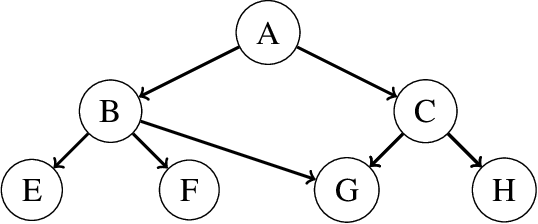
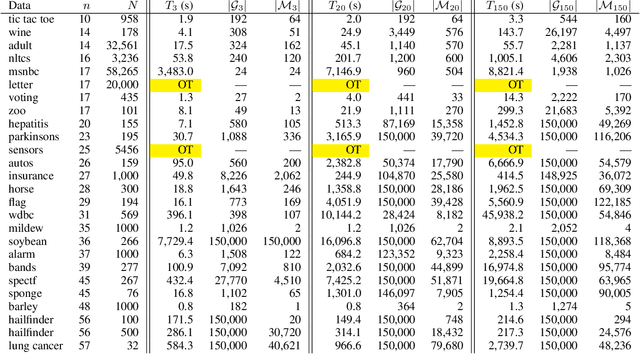
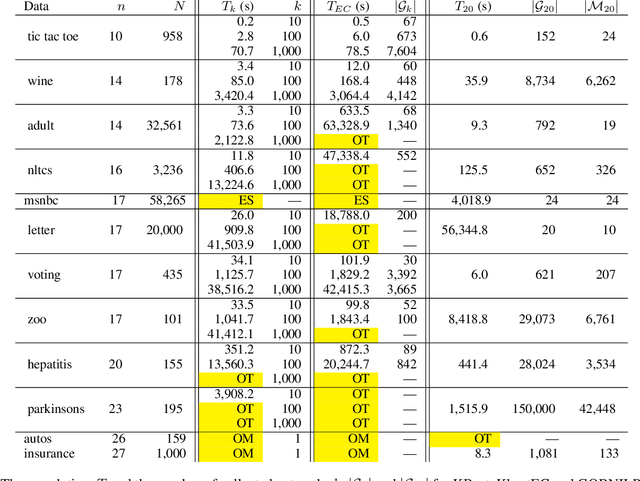
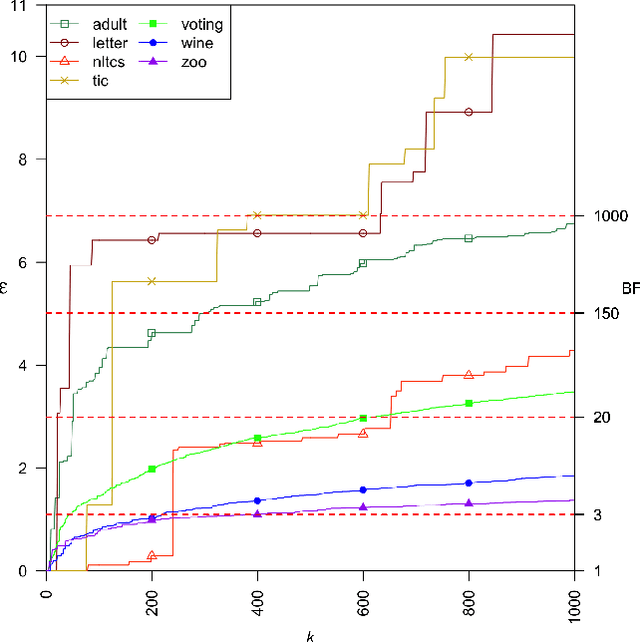
A Bayesian network is a widely used probabilistic graphical model with applications in knowledge discovery and prediction. Learning a Bayesian network (BN) from data can be cast as an optimization problem using the well-known score-and-search approach. However, selecting a single model (i.e., the best scoring BN) can be misleading or may not achieve the best possible accuracy. An alternative to committing to a single model is to perform some form of Bayesian or frequentist model averaging, where the space of possible BNs is sampled or enumerated in some fashion. Unfortunately, existing approaches for model averaging either severely restrict the structure of the Bayesian network or have only been shown to scale to networks with fewer than 30 random variables. In this paper, we propose a novel approach to model averaging inspired by performance guarantees in approximation algorithms. Our approach has two primary advantages. First, our approach only considers credible models in that they are optimal or near-optimal in score. Second, our approach is more efficient and scales to significantly larger Bayesian networks than existing approaches.