Scalable Bayesian Network Structure Learning with Splines

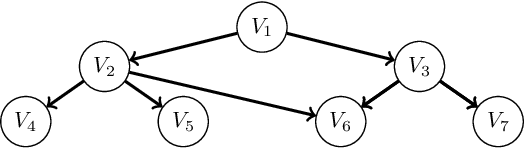
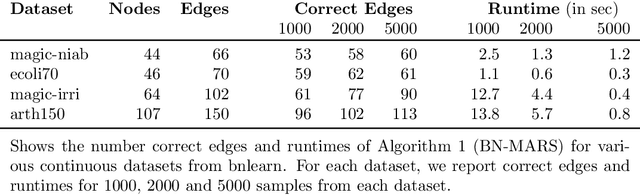
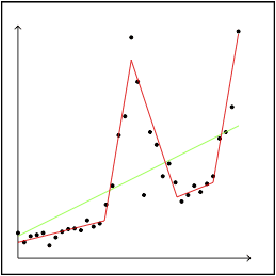
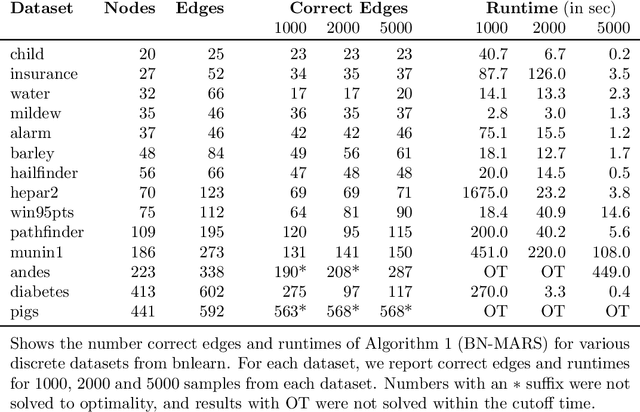
A Bayesian Network (BN) is a probabilistic graphical model consisting of a directed acyclic graph (DAG), where each node is a random variable represented as a function of its parents. We present a novel approach capable of learning the global DAG structure of a BN and modelling linear and non-linear local relationships between variables. We achieve this by a combination of feature selection to reduce the search space for local relationships, and extending the widely used score-and-search approach to support modelling relationships between variables as Multivariate Adaptive Regression Splines (MARS). MARS are polynomial regression models represented as piecewise spline functions - this lets us model non-linear relationships without the risk of overfitting that a single polynomial regression model would bring. The combination allows us to learn relationships in all bnlearn benchmark instances within minutes and enables us to scale to networks of over a thousand nodes

A Score-and-Search Approach to Learning Bayesian Networks with Noisy-OR Relations

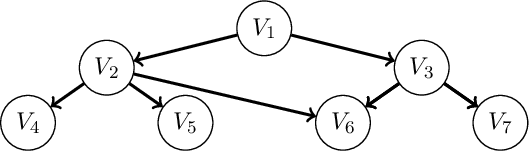
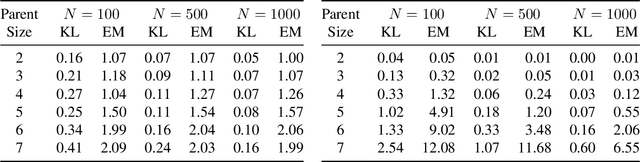
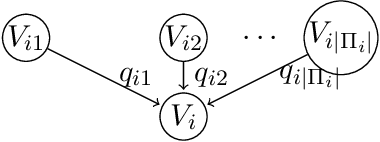
A Bayesian network is a probabilistic graphical model that consists of a directed acyclic graph (DAG), where each node is a random variable and attached to each node is a conditional probability distribution (CPD). A Bayesian network can be learned from data using the well-known score-and-search approach, and within this approach a key consideration is how to simultaneously learn the global structure in the form of the underlying DAG and the local structure in the CPDs. Several useful forms of local structure have been identified in the literature but thus far the score-and-search approach has only been extended to handle local structure in form of context-specific independence. In this paper, we show how to extend the score-and-search approach to the important and widely useful case of noisy-OR relations. We provide an effective gradient descent algorithm to score a candidate noisy-OR using the widely used BIC score and we provide pruning rules that allow the search to successfully scale to medium sized networks. Our empirical results provide evidence for the success of our approach to learning Bayesian networks that incorporate noisy-OR relations.

Learning All Credible Bayesian Network Structures for Model Averaging

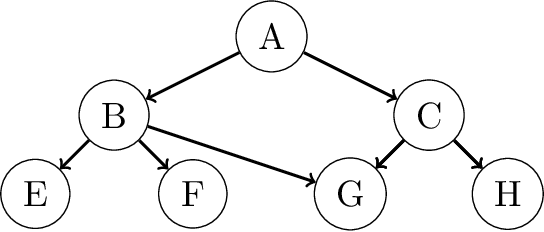
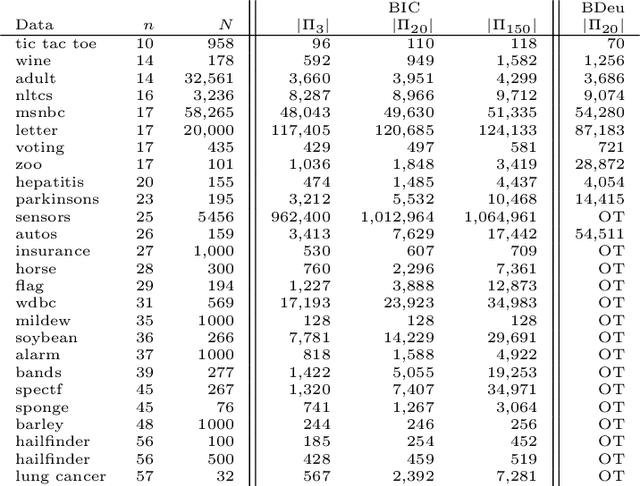
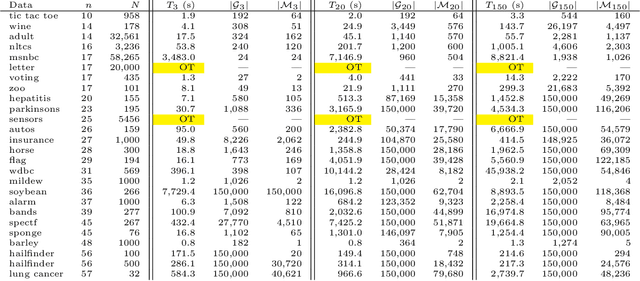
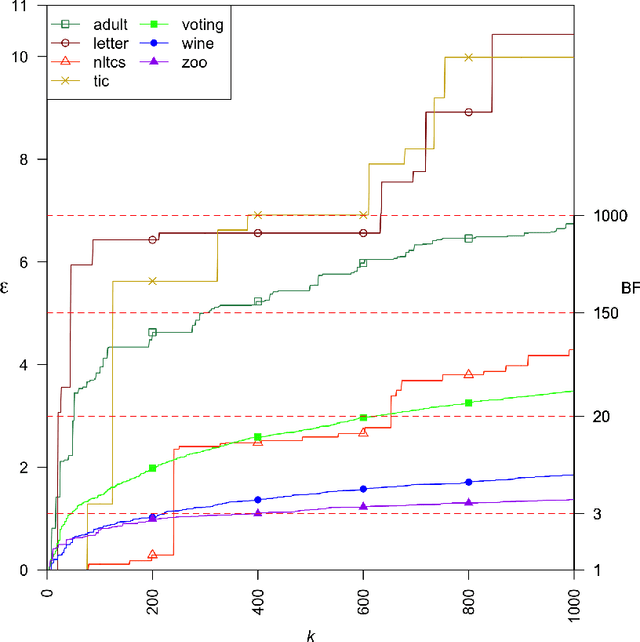
A Bayesian network is a widely used probabilistic graphical model with applications in knowledge discovery and prediction. Learning a Bayesian network (BN) from data can be cast as an optimization problem using the well-known score-and-search approach. However, selecting a single model (i.e., the best scoring BN) can be misleading or may not achieve the best possible accuracy. An alternative to committing to a single model is to perform some form of Bayesian or frequentist model averaging, where the space of possible BNs is sampled or enumerated in some fashion. Unfortunately, existing approaches for model averaging either severely restrict the structure of the Bayesian network or have only been shown to scale to networks with fewer than 30 random variables. In this paper, we propose a novel approach to model averaging inspired by performance guarantees in approximation algorithms. Our approach has two primary advantages. First, our approach only considers credible models in that they are optimal or near-optimal in score. Second, our approach is more efficient and scales to significantly larger Bayesian networks than existing approaches.

Finding All Bayesian Network Structures within a Factor of Optimal

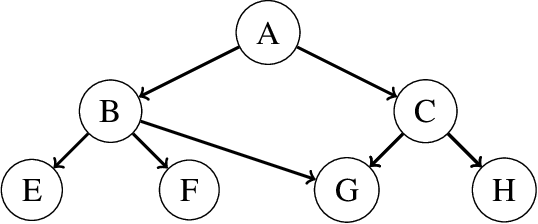
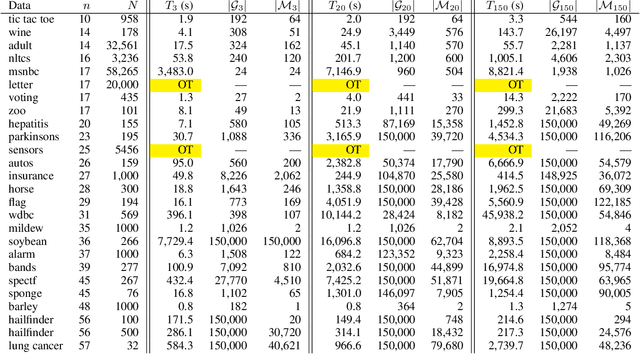
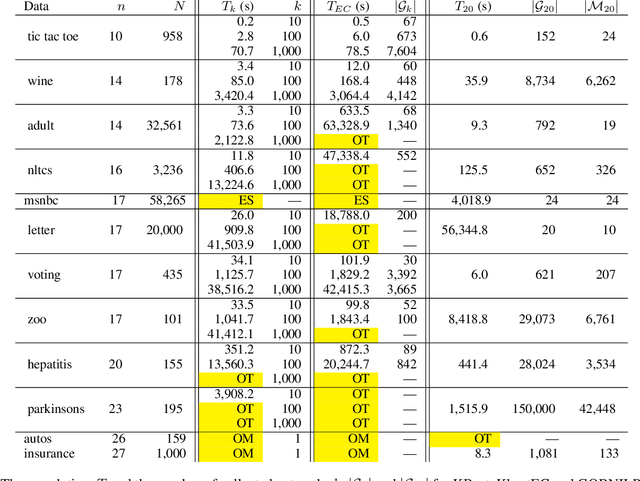
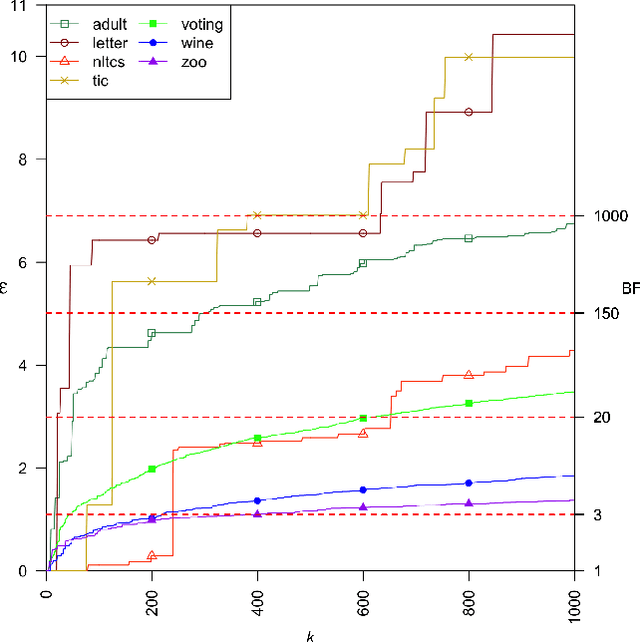
A Bayesian network is a widely used probabilistic graphical model with applications in knowledge discovery and prediction. Learning a Bayesian network (BN) from data can be cast as an optimization problem using the well-known score-and-search approach. However, selecting a single model (i.e., the best scoring BN) can be misleading or may not achieve the best possible accuracy. An alternative to committing to a single model is to perform some form of Bayesian or frequentist model averaging, where the space of possible BNs is sampled or enumerated in some fashion. Unfortunately, existing approaches for model averaging either severely restrict the structure of the Bayesian network or have only been shown to scale to networks with fewer than 30 random variables. In this paper, we propose a novel approach to model averaging inspired by performance guarantees in approximation algorithms. Our approach has two primary advantages. First, our approach only considers credible models in that they are optimal or near-optimal in score. Second, our approach is more efficient and scales to significantly larger Bayesian networks than existing approaches.

Improved Image Selection for Stack-Based HDR Imaging

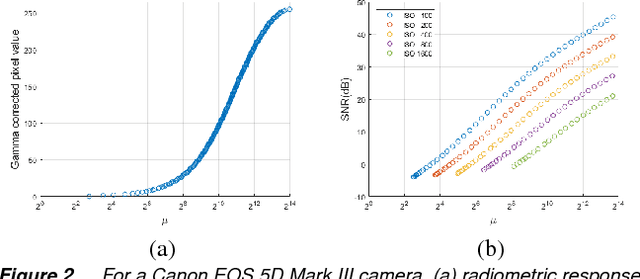
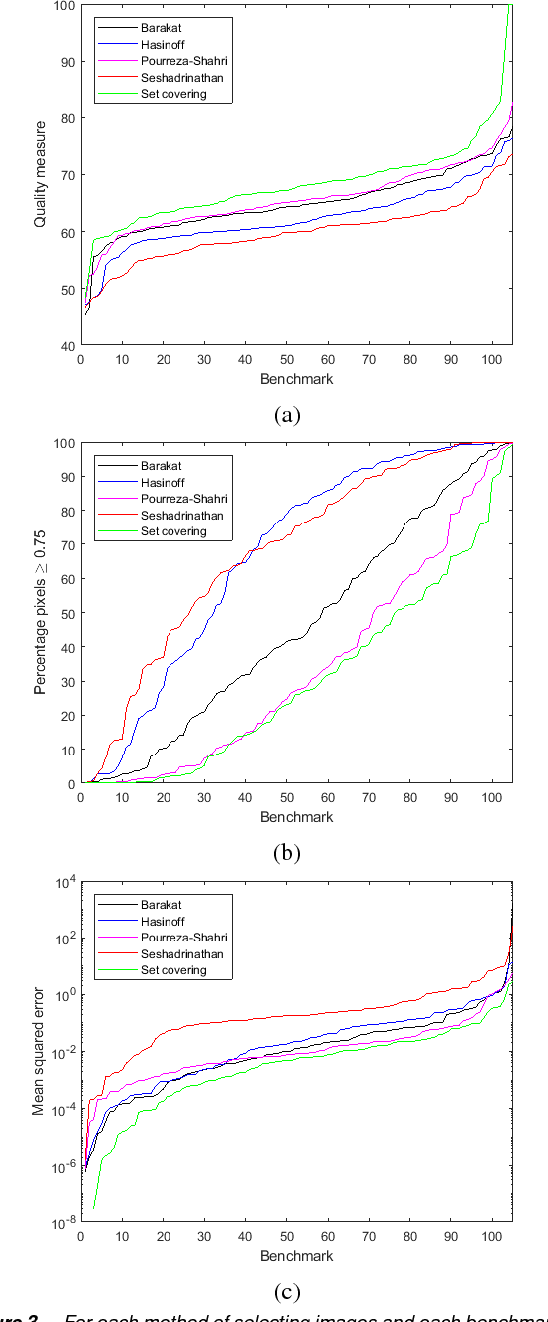
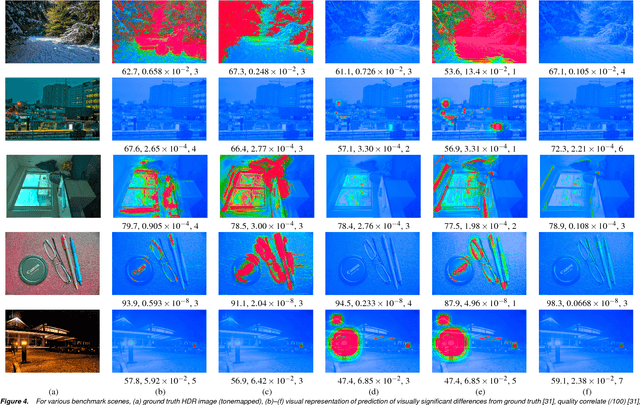
Stack-based high dynamic range (HDR) imaging is a technique for achieving a larger dynamic range in an image by combining several low dynamic range images acquired at different exposures. Minimizing the set of images to combine, while ensuring that the resulting HDR image fully captures the scene's irradiance, is important to avoid long image acquisition and post-processing times. The problem of selecting the set of images has received much attention. However, existing methods either are not fully automatic, can be slow, or can fail to fully capture more challenging scenes. In this paper, we propose a fully automatic method for selecting the set of exposures to acquire that is both fast and more accurate. We show on an extensive set of benchmark scenes that our proposed method leads to improved HDR images as measured against ground truth using the mean squared error, a pixel-based metric, and a visible difference predictor and a quality score, both perception-based metrics.

Illuminant Estimation using Ensembles of Multivariate Regression Trees

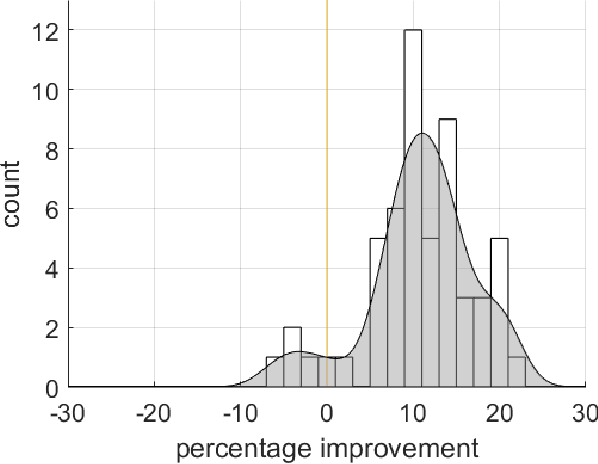
White balancing is a fundamental step in the image processing pipeline. The process involves estimating the chromaticity of the illuminant or light source and using the estimate to correct the image to remove any color cast. Given the importance of the problem, there has been much previous work on illuminant estimation. Recently, an approach based on ensembles of univariate regression trees that are fit using the squared-error loss function has been proposed and shown to give excellent performance. In this paper, we show that a simpler and more accurate ensemble model can be learned by (i) using multivariate regression trees to take into account that the chromaticity components of the illuminant are correlated and constrained, and (ii) fitting each tree by directly minimizing a loss function of interest---such as recovery angular error or reproduction angular error---rather than indirectly using the squared-error loss function as a surrogate. We show empirically that overall our method leads to improved performance on diverse image sets.

Exploiting Structure in Weighted Model Counting Approaches to Probabilistic Inference

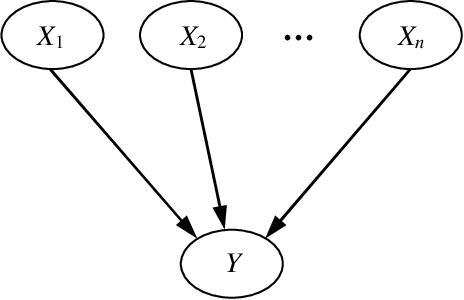
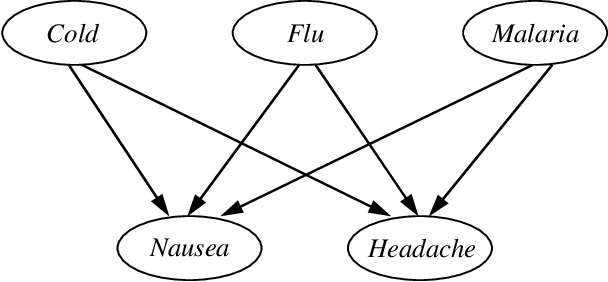
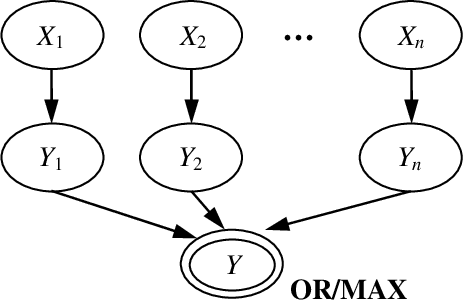
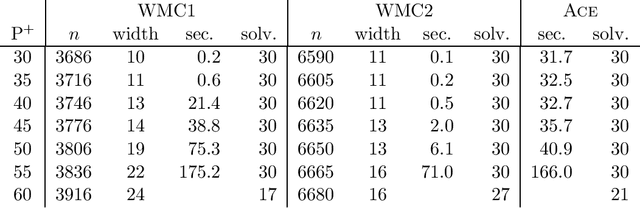
Previous studies have demonstrated that encoding a Bayesian network into a SAT formula and then performing weighted model counting using a backtracking search algorithm can be an effective method for exact inference. In this paper, we present techniques for improving this approach for Bayesian networks with noisy-OR and noisy-MAX relations---two relations that are widely used in practice as they can dramatically reduce the number of probabilities one needs to specify. In particular, we present two SAT encodings for noisy-OR and two encodings for noisy-MAX that exploit the structure or semantics of the relations to improve both time and space efficiency, and we prove the correctness of the encodings. We experimentally evaluated our techniques on large-scale real and randomly generated Bayesian networks. On these benchmarks, our techniques gave speedups of up to two orders of magnitude over the best previous approaches for networks with noisy-OR/MAX relations and scaled up to larger networks. As well, our techniques extend the weighted model counting approach for exact inference to networks that were previously intractable for the approach.