Balancing central and marginal rejection when combining independent significance tests

A common approach to evaluating the significance of a collection of $p$-values combines them with a pooling function, in particular when the original data are not available. These pooled $p$-values convert a sample of $p$-values into a single number which behaves like a univariate $p$-value. To clarify discussion of these functions, a telescoping series of alternative hypotheses are introduced that communicate the strength and prevalence of non-null evidence in the $p$-values before general pooling formulae are discussed. A pattern noticed in the UMP pooled $p$-value for a particular alternative motivates the definition and discussion of central and marginal rejection levels at $\alpha$. It is proven that central rejection is always greater than or equal to marginal rejection, motivating a quotient to measure the balance between the two for pooled $p$-values. A combining function based on the $\chi^2_{\kappa}$ quantile transformation is proposed to control this quotient and shown to be robust to mis-specified parameters relative to the UMP. Different powers for different parameter settings motivate a map of plausible alternatives based on where this pooled $p$-value is minimized.

Illuminant Estimation using Ensembles of Multivariate Regression Trees

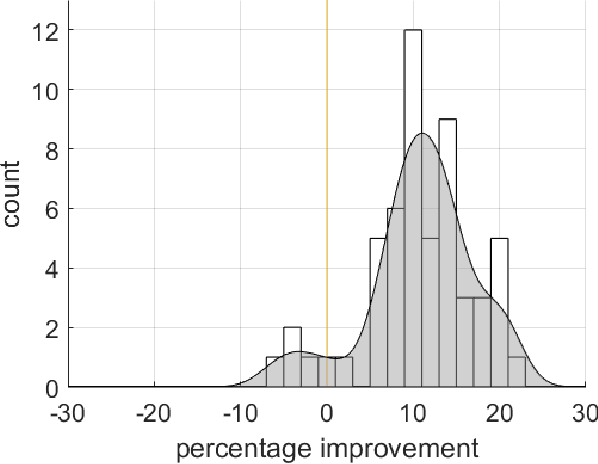
White balancing is a fundamental step in the image processing pipeline. The process involves estimating the chromaticity of the illuminant or light source and using the estimate to correct the image to remove any color cast. Given the importance of the problem, there has been much previous work on illuminant estimation. Recently, an approach based on ensembles of univariate regression trees that are fit using the squared-error loss function has been proposed and shown to give excellent performance. In this paper, we show that a simpler and more accurate ensemble model can be learned by (i) using multivariate regression trees to take into account that the chromaticity components of the illuminant are correlated and constrained, and (ii) fitting each tree by directly minimizing a loss function of interest---such as recovery angular error or reproduction angular error---rather than indirectly using the squared-error loss function as a surrogate. We show empirically that overall our method leads to improved performance on diverse image sets.