Scalable Bayesian Network Structure Learning with Splines
Paper and Code
Oct 27, 2021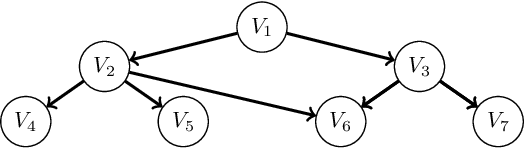
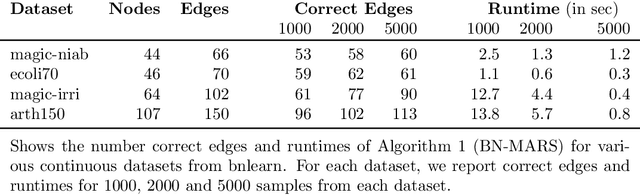
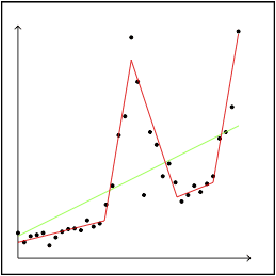
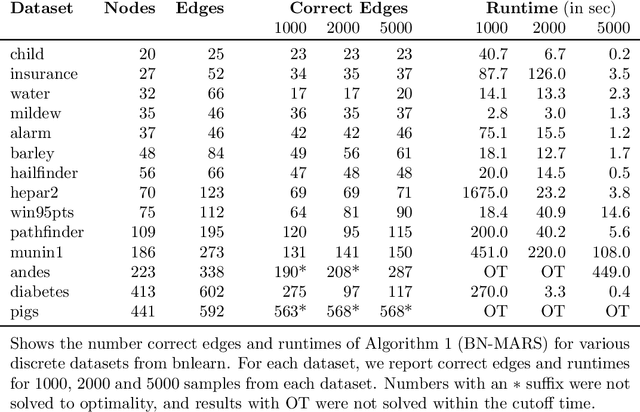
A Bayesian Network (BN) is a probabilistic graphical model consisting of a directed acyclic graph (DAG), where each node is a random variable represented as a function of its parents. We present a novel approach capable of learning the global DAG structure of a BN and modelling linear and non-linear local relationships between variables. We achieve this by a combination of feature selection to reduce the search space for local relationships, and extending the widely used score-and-search approach to support modelling relationships between variables as Multivariate Adaptive Regression Splines (MARS). MARS are polynomial regression models represented as piecewise spline functions - this lets us model non-linear relationships without the risk of overfitting that a single polynomial regression model would bring. The combination allows us to learn relationships in all bnlearn benchmark instances within minutes and enables us to scale to networks of over a thousand nodes
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge