On Pruning for Score-Based Bayesian Network Structure Learning

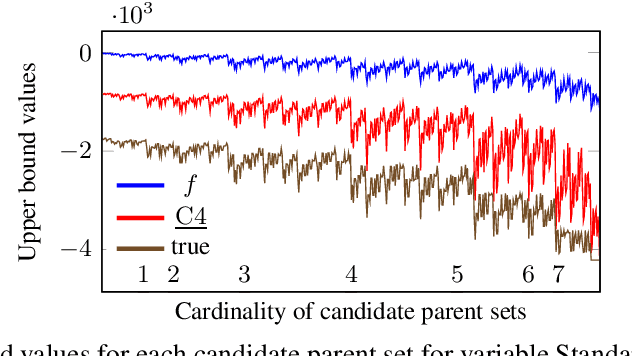
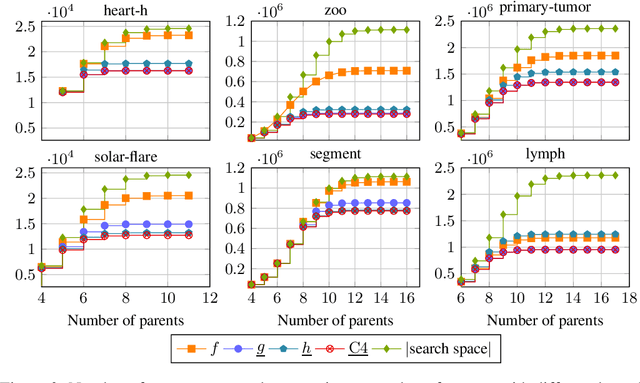
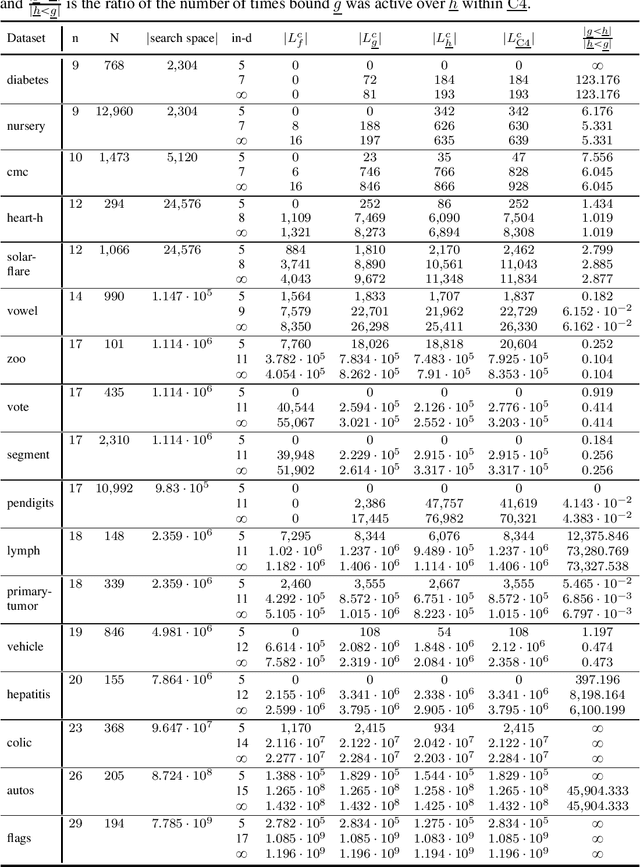
Many algorithms for score-based Bayesian network structure learning (BNSL) take as input a collection of potentially optimal parent sets for each variable in a data set. Constructing these collections naively is computationally intensive since the number of parent sets grows exponentially with the number of variables. Therefore, pruning techniques are not only desirable but essential. While effective pruning exists for the Bayesian Information Criterion (BIC), current results for the Bayesian Dirichlet equivalent uniform (BDeu) score reduce the search space very modestly, hampering the use of (the often preferred) BDeu. We derive new non-trivial theoretical upper bounds for the BDeu score that considerably improve on the state of the art. Since the new bounds are efficient and easy to implement, they can be promptly integrated into many BNSL methods. We show that gains can be significant in multiple UCI data sets so as to highlight practical implications of the theoretical advances.