Alvaro H. C. Correia
Fundamental bounds on efficiency-confidence trade-off for transductive conformal prediction
Sep 04, 2025Abstract:Transductive conformal prediction addresses the simultaneous prediction for multiple data points. Given a desired confidence level, the objective is to construct a prediction set that includes the true outcomes with the prescribed confidence. We demonstrate a fundamental trade-off between confidence and efficiency in transductive methods, where efficiency is measured by the size of the prediction sets. Specifically, we derive a strict finite-sample bound showing that any non-trivial confidence level leads to exponential growth in prediction set size for data with inherent uncertainty. The exponent scales linearly with the number of samples and is proportional to the conditional entropy of the data. Additionally, the bound includes a second-order term, dispersion, defined as the variance of the log conditional probability distribution. We show that this bound is achievable in an idealized setting. Finally, we examine a special case of transductive prediction where all test data points share the same label. We show that this scenario reduces to the hypothesis testing problem with empirically observed statistics and provide an asymptotically optimal confidence predictor, along with an analysis of the error exponent.
Approximating Full Conformal Prediction for Neural Network Regression with Gauss-Newton Influence
Jul 27, 2025Abstract:Uncertainty quantification is an important prerequisite for the deployment of deep learning models in safety-critical areas. Yet, this hinges on the uncertainty estimates being useful to the extent the prediction intervals are well-calibrated and sharp. In the absence of inherent uncertainty estimates (e.g. pretrained models predicting only point estimates), popular approaches that operate post-hoc include Laplace's method and split conformal prediction (split-CP). However, Laplace's method can be miscalibrated when the model is misspecified and split-CP requires sample splitting, and thus comes at the expense of statistical efficiency. In this work, we construct prediction intervals for neural network regressors post-hoc without held-out data. This is achieved by approximating the full conformal prediction method (full-CP). Whilst full-CP nominally requires retraining the model for every test point and candidate label, we propose to train just once and locally perturb model parameters using Gauss-Newton influence to approximate the effect of retraining. Coupled with linearization of the network, we express the absolute residual nonconformity score as a piecewise linear function of the candidate label allowing for an efficient procedure that avoids the exhaustive search over the output space. On standard regression benchmarks and bounding box localization, we show the resulting prediction intervals are locally-adaptive and often tighter than those of split-CP.
Continuous Mixtures of Tractable Probabilistic Models
Sep 21, 2022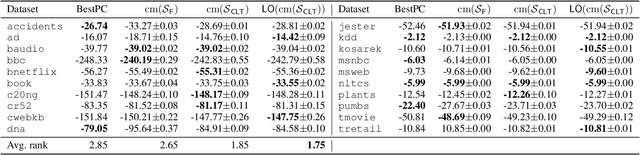
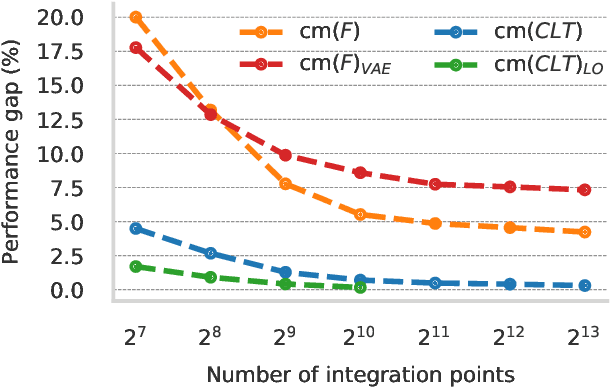


Abstract:Probabilistic models based on continuous latent spaces, such as variational autoencoders, can be understood as uncountable mixture models where components depend continuously on the latent code. They have proven expressive tools for generative and probabilistic modelling, but are at odds with tractable probabilistic inference, that is, computing marginals and conditionals of the represented probability distribution. Meanwhile, tractable probabilistic models such as probabilistic circuits (PCs) can be understood as hierarchical discrete mixture models, which allows them to perform exact inference, but often they show subpar performance in comparison to continuous latent-space models. In this paper, we investigate a hybrid approach, namely continuous mixtures of tractable models with a small latent dimension. While these models are analytically intractable, they are well amenable to numerical integration schemes based on a finite set of integration points. With a large enough number of integration points the approximation becomes de-facto exact. Moreover, using a finite set of integration points, the approximation method can be compiled into a PC performing `exact inference in an approximate model'. In experiments, we show that this simple scheme proves remarkably effective, as PCs learned this way set new state-of-the-art for tractable models on many standard density estimation benchmarks.
Neural Simulated Annealing
Mar 04, 2022



Abstract:Simulated annealing (SA) is a stochastic global optimisation technique applicable to a wide range of discrete and continuous variable problems. Despite its simplicity, the development of an effective SA optimiser for a given problem hinges on a handful of carefully handpicked components; namely, neighbour proposal distribution and temperature annealing schedule. In this work, we view SA from a reinforcement learning perspective and frame the proposal distribution as a policy, which can be optimised for higher solution quality given a fixed computational budget. We demonstrate that this Neural SA with such a learnt proposal distribution, parametrised by small equivariant neural networks, outperforms SA baselines on a number of problems: Rosenbrock's function, the Knapsack problem, the Bin Packing problem, and the Travelling Salesperson problem. We also show that Neural SA scales well to large problems - generalising to significantly larger problems than the ones seen during training - while achieving comparable performance to popular off-the-shelf solvers and other machine learning methods in terms of solution quality and wall-clock time.
Joints in Random Forests
Jul 11, 2020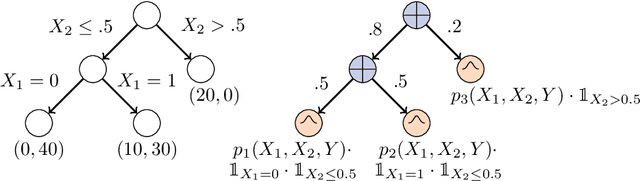
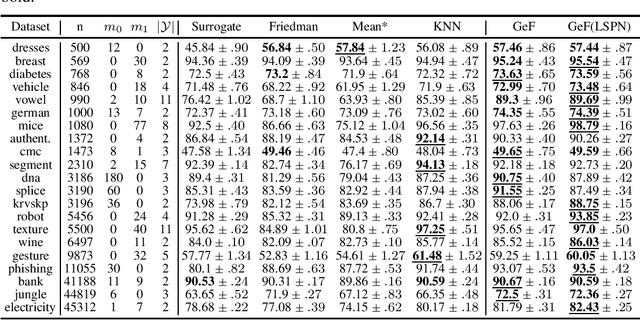
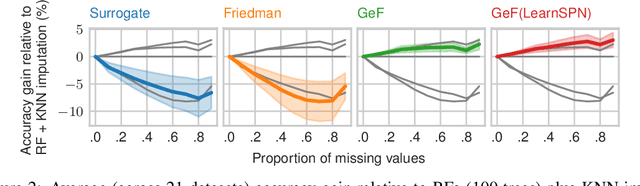
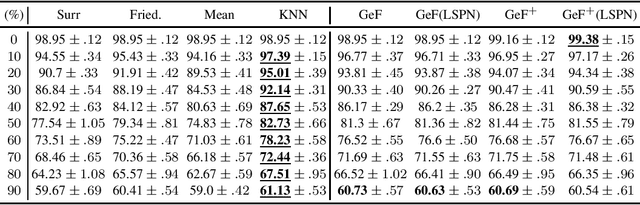
Abstract:Decision Trees (DTs) and Random Forests (RFs) are powerful discriminative learners and tools of central importance to the everyday machine learning practitioner and data scientist. Due to their discriminative nature, however, they lack principled methods to process inputs with missing features or to detect outliers, which requires pairing them with imputation techniques or a separate generative model. In this paper, we demonstrate that DTs and RFs can naturally be interpreted as generative models, by drawing a connection to Probabilistic Circuits, a prominent class of tractable probabilistic models. This reinterpretation equips them with a full joint distribution over the feature space and leads to Generative Decision Trees (GeDTs) and Generative Forests (GeFs), a family of novel hybrid generative-discriminative models. This family of models retains the overall characteristics of DTs and RFs while additionally being able to handle missing features by means of marginalisation. Under certain assumptions, frequently made for Bayes consistency results, we show that consistency in GeDTs and GeFs extend to any pattern of missing input features, if missing at random. Empirically, we show that our models often outperform common routines to treat missing data, such as K-nearest neighbour imputation, and moreover, that our models can naturally detect outliers by monitoring the marginal probability of input features.
Towards Robust Classification with Deep Generative Forests
Jul 11, 2020



Abstract:Decision Trees and Random Forests are among the most widely used machine learning models, and often achieve state-of-the-art performance in tabular, domain-agnostic datasets. Nonetheless, being primarily discriminative models they lack principled methods to manipulate the uncertainty of predictions. In this paper, we exploit Generative Forests (GeFs), a recent class of deep probabilistic models that addresses these issues by extending Random Forests to generative models representing the full joint distribution over the feature space. We demonstrate that GeFs are uncertainty-aware classifiers, capable of measuring the robustness of each prediction as well as detecting out-of-distribution samples.
On Pruning for Score-Based Bayesian Network Structure Learning
May 23, 2019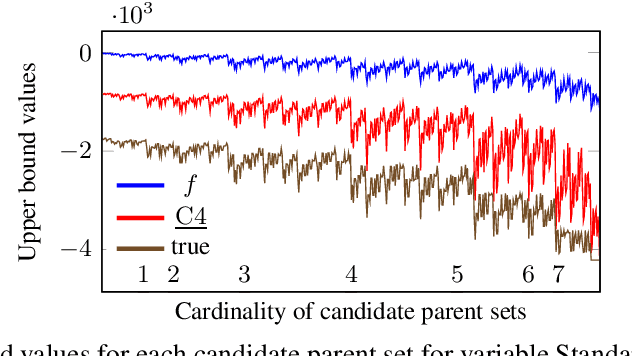
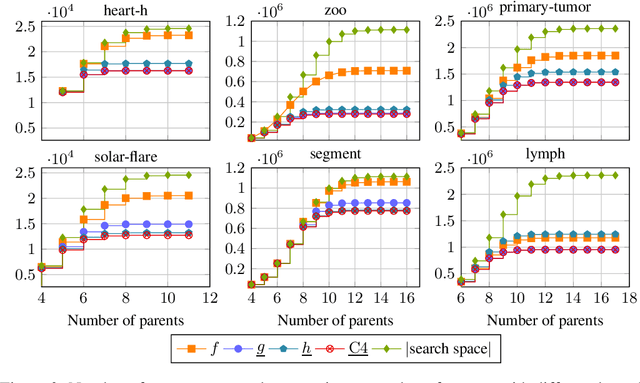
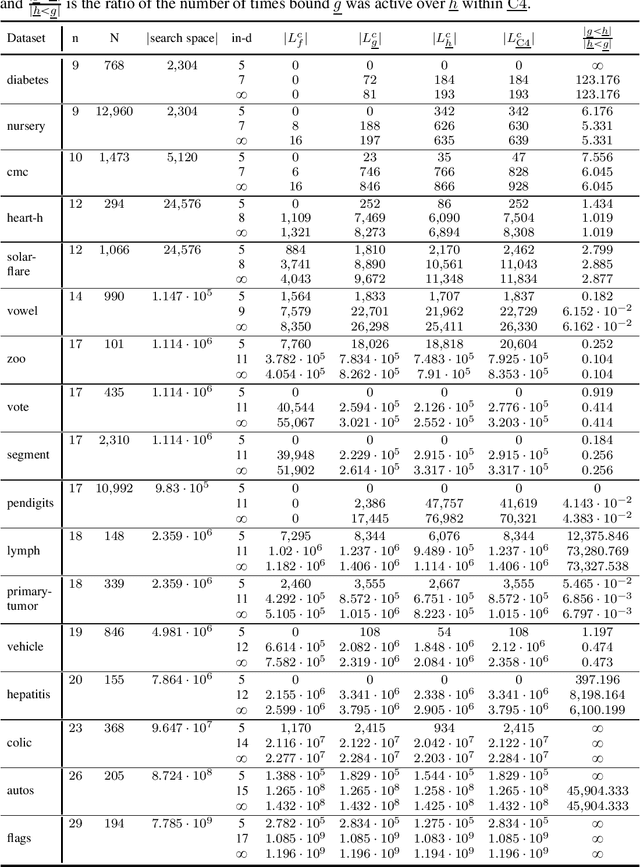
Abstract:Many algorithms for score-based Bayesian network structure learning (BNSL) take as input a collection of potentially optimal parent sets for each variable in a data set. Constructing these collections naively is computationally intensive since the number of parent sets grows exponentially with the number of variables. Therefore, pruning techniques are not only desirable but essential. While effective pruning exists for the Bayesian Information Criterion (BIC), current results for the Bayesian Dirichlet equivalent uniform (BDeu) score reduce the search space very modestly, hampering the use of (the often preferred) BDeu. We derive new non-trivial theoretical upper bounds for the BDeu score that considerably improve on the state of the art. Since the new bounds are efficient and easy to implement, they can be promptly integrated into many BNSL methods. We show that gains can be significant in multiple UCI data sets so as to highlight practical implications of the theoretical advances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge