Improved Communication Lower Bounds for Distributed Optimisation

Motivated by the interest in communication-efficient methods for distributed machine learning, we consider the communication complexity of minimising a sum of $d$-dimensional functions $\sum_{i = 1}^N f_i (x)$, where each function $f_i$ is held by a one of the $N$ different machines. Such tasks arise naturally in large-scale optimisation, where a standard solution is to apply variants of (stochastic) gradient descent. As our main result, we show that $\Omega( Nd \log d / \varepsilon)$ bits in total need to be communicated between the machines to find an additive $\epsilon$-approximation to the minimum of $\sum_{i = 1}^N f_i (x)$. The results holds for deterministic algorithms, and randomised algorithms under some restrictions on the parameter values. Importantly, our lower bounds require no assumptions on the structure of the algorithm, and are matched within constant factors for strongly convex objectives by a new variant of quantised gradient descent. The lower bounds are obtained by bringing over tools from communication complexity to distributed optimisation, an approach we hope will find further use in future.

Relaxed Scheduling for Scalable Belief Propagation

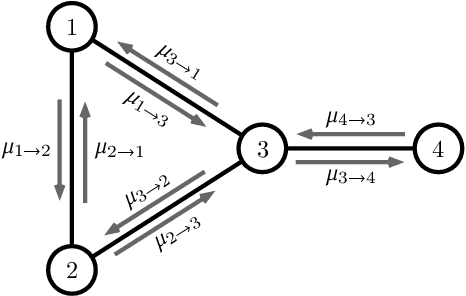
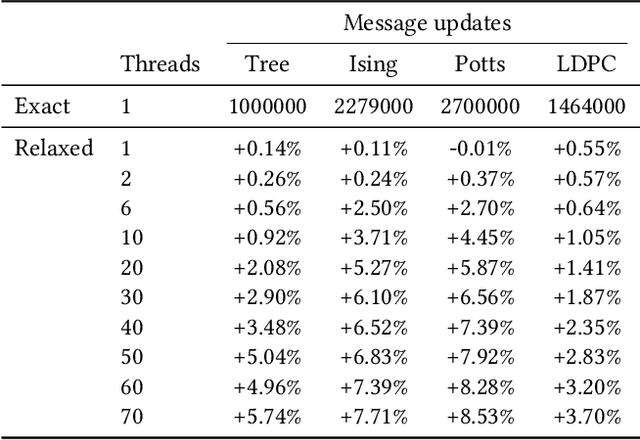
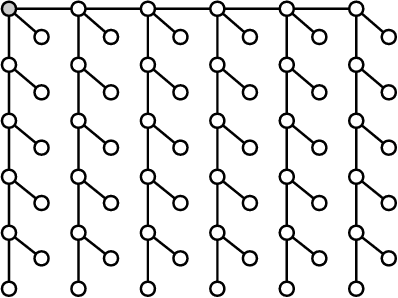
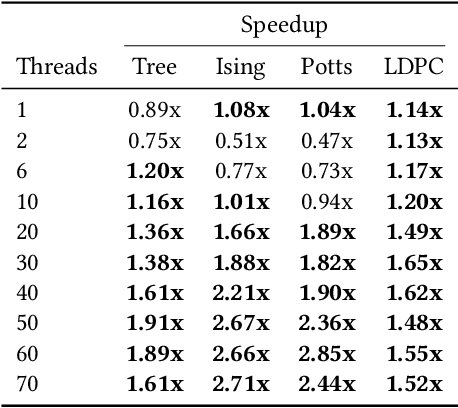
The ability to leverage large-scale hardware parallelism has been one of the key enablers of the accelerated recent progress in machine learning. Consequently, there has been considerable effort invested into developing efficient parallel variants of classic machine learning algorithms. However, despite the wealth of knowledge on parallelization, some classic machine learning algorithms often prove hard to parallelize efficiently while maintaining convergence. In this paper, we focus on efficient parallel algorithms for the key machine learning task of inference on graphical models, in particular on the fundamental belief propagation algorithm. We address the challenge of efficiently parallelizing this classic paradigm by showing how to leverage scalable relaxed schedulers in this context. We present an extensive empirical study, showing that our approach outperforms previous parallel belief propagation implementations both in terms of scalability and in terms of wall-clock convergence time, on a range of practical applications.

Bayesian Network Structure Learning with Integer Programming: Polytopes, Facets, and Complexity

The challenging task of learning structures of probabilistic graphical models is an important problem within modern AI research. Recent years have witnessed several major algorithmic advances in structure learning for Bayesian networks---arguably the most central class of graphical models---especially in what is known as the score-based setting. A successful generic approach to optimal Bayesian network structure learning (BNSL), based on integer programming (IP), is implemented in the GOBNILP system. Despite the recent algorithmic advances, current understanding of foundational aspects underlying the IP based approach to BNSL is still somewhat lacking. Understanding fundamental aspects of cutting planes and the related separation problem( is important not only from a purely theoretical perspective, but also since it holds out the promise of further improving the efficiency of state-of-the-art approaches to solving BNSL exactly. In this paper, we make several theoretical contributions towards these goals: (i) we study the computational complexity of the separation problem, proving that the problem is NP-hard; (ii) we formalise and analyse the relationship between three key polytopes underlying the IP-based approach to BNSL; (iii) we study the facets of the three polytopes both from the theoretical and practical perspective, providing, via exhaustive computation, a complete enumeration of facets for low-dimensional family-variable polytopes; and, furthermore, (iv) we establish a tight connection of the BNSL problem to the acyclic subgraph problem.