Derivative-based regularization for regression

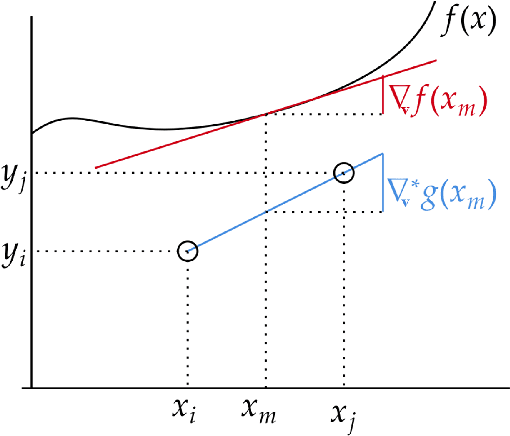
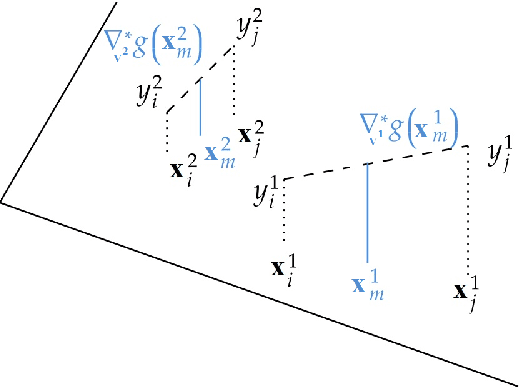
In this work, we introduce a novel approach to regularization in multivariable regression problems. Our regularizer, called DLoss, penalises differences between the model's derivatives and derivatives of the data generating function as estimated from the training data. We call these estimated derivatives data derivatives. The goal of our method is to align the model to the data, not only in terms of target values but also in terms of the derivatives involved. To estimate data derivatives, we select (from the training data) 2-tuples of input-value pairs, using either nearest neighbour or random, selection. On synthetic and real datasets, we evaluate the effectiveness of adding DLoss, with different weights, to the standard mean squared error loss. The experimental results show that with DLoss (using nearest neighbour selection) we obtain, on average, the best rank with respect to MSE on validation data sets, compared to no regularization, L2 regularization, and Dropout.

Relaxed Scheduling for Scalable Belief Propagation

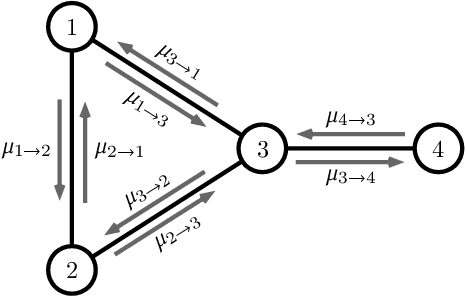
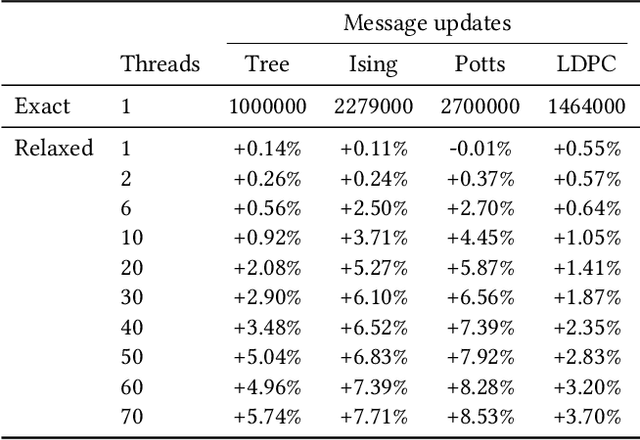
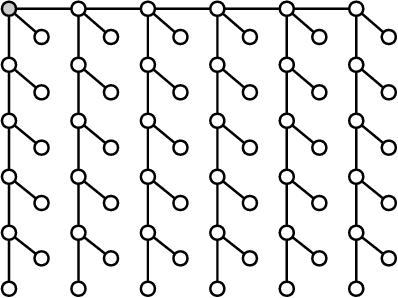
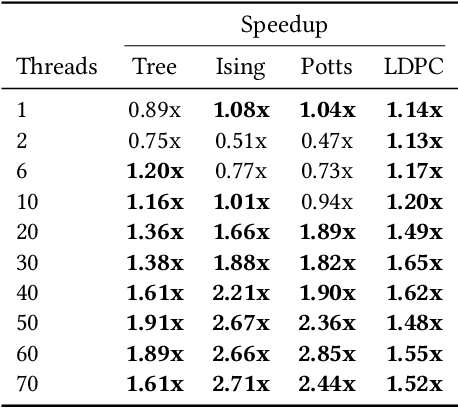
The ability to leverage large-scale hardware parallelism has been one of the key enablers of the accelerated recent progress in machine learning. Consequently, there has been considerable effort invested into developing efficient parallel variants of classic machine learning algorithms. However, despite the wealth of knowledge on parallelization, some classic machine learning algorithms often prove hard to parallelize efficiently while maintaining convergence. In this paper, we focus on efficient parallel algorithms for the key machine learning task of inference on graphical models, in particular on the fundamental belief propagation algorithm. We address the challenge of efficiently parallelizing this classic paradigm by showing how to leverage scalable relaxed schedulers in this context. We present an extensive empirical study, showing that our approach outperforms previous parallel belief propagation implementations both in terms of scalability and in terms of wall-clock convergence time, on a range of practical applications.

PopSGD: Decentralized Stochastic Gradient Descent in the Population Model

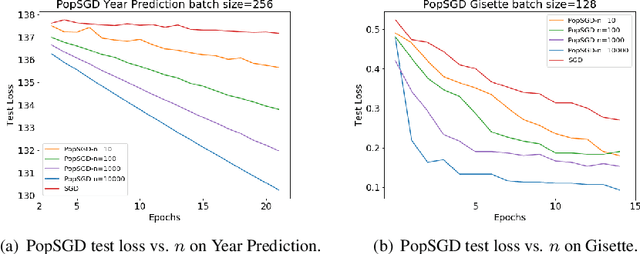
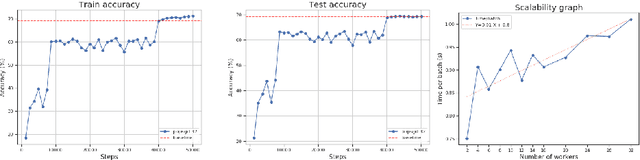
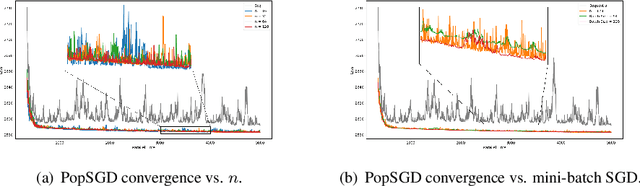
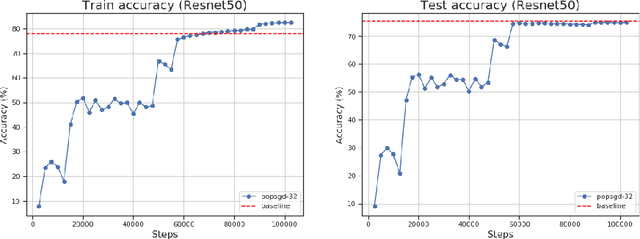
The population model is a standard way to represent large-scale decentralized distributed systems, in which agents with limited computational power interact in randomly chosen pairs, in order to collectively solve global computational tasks. In contrast with synchronous gossip models, nodes are anonymous, lack a common notion of time, and have no control over their scheduling. In this paper, we examine whether large-scale distributed optimization can be performed in this extremely restrictive setting. We introduce and analyze a natural decentralized variant of stochastic gradient descent (SGD), called PopSGD, in which every node maintains a local parameter, and is able to compute stochastic gradients with respect to this parameter. Every pair-wise node interaction performs a stochastic gradient step at each agent, followed by averaging of the two models. We prove that, under standard assumptions, SGD can converge even in this extremely loose, decentralized setting, for both convex and non-convex objectives. Moreover, surprisingly, in the former case, the algorithm can achieve linear speedup in the number of nodes $n$. Our analysis leverages a new technical connection between decentralized SGD and randomized load-balancing, which enables us to tightly bound the concentration of node parameters. We validate our analysis through experiments, showing that PopSGD can achieve convergence and speedup for large-scale distributed learning tasks in a supercomputing environment.