Hybrid Decentralized Optimization: First- and Zeroth-Order Optimizers Can Be Jointly Leveraged For Faster Convergence

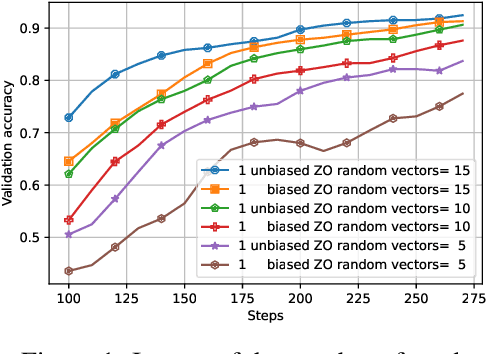
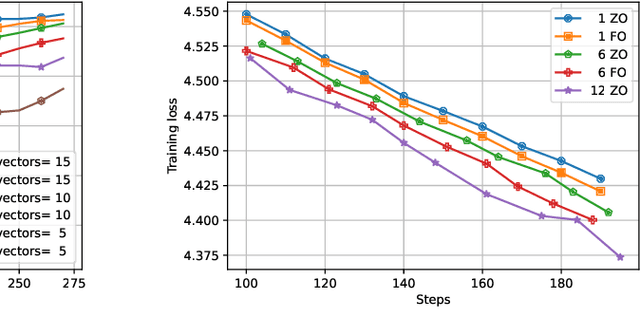
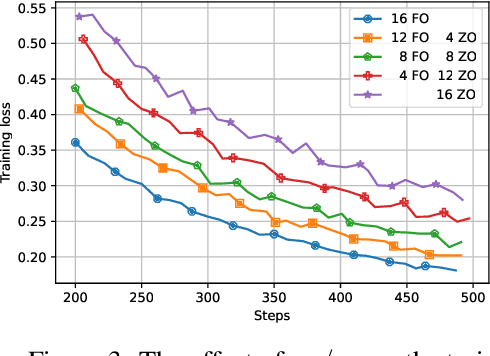
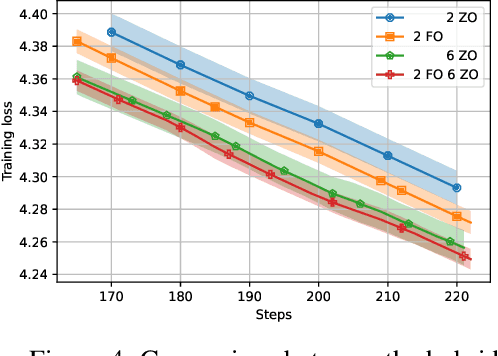
Distributed optimization has become one of the standard ways of speeding up machine learning training, and most of the research in the area focuses on distributed first-order, gradient-based methods. Yet, there are settings where some computationally-bounded nodes may not be able to implement first-order, gradient-based optimization, while they could still contribute to joint optimization tasks. In this paper, we initiate the study of hybrid decentralized optimization, studying settings where nodes with zeroth-order and first-order optimization capabilities co-exist in a distributed system, and attempt to jointly solve an optimization task over some data distribution. We essentially show that, under reasonable parameter settings, such a system can not only withstand noisier zeroth-order agents but can even benefit from integrating such agents into the optimization process, rather than ignoring their information. At the core of our approach is a new analysis of distributed optimization with noisy and possibly-biased gradient estimators, which may be of independent interest. Experimental results on standard optimization tasks confirm our analysis, showing that hybrid first-zeroth order optimization can be practical.

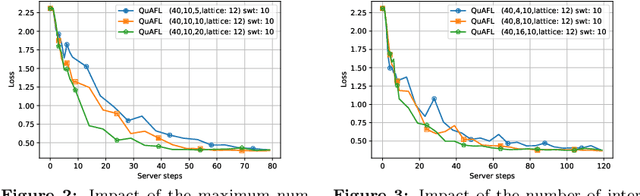
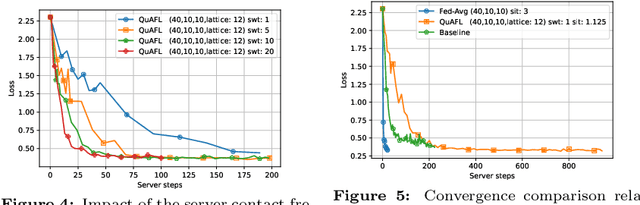
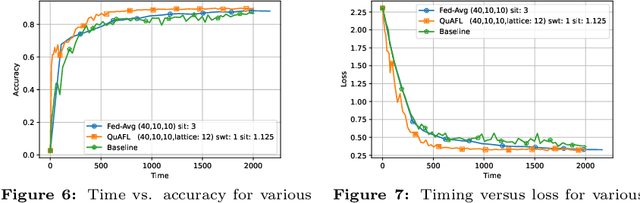
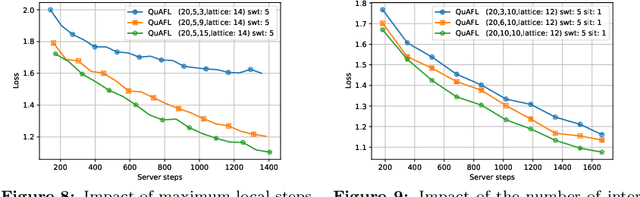
QuAFL: Federated Averaging Can Be Both Asynchronous and Communication-Efficient

Federated Learning (FL) is an emerging paradigm to enable the large-scale distributed training of machine learning models, while still providing privacy guarantees. In this work, we jointly address two of the main practical challenges when scaling federated optimization to large node counts: the need for tight synchronization between the central authority and individual computing nodes, and the large communication cost of transmissions between the central server and clients. Specifically, we present a new variant of the classic federated averaging (FedAvg) algorithm, which supports both asynchronous communication and communication compression. We provide a new analysis technique showing that, in spite of these system relaxations, our algorithm essentially matches the best known bounds for FedAvg, under reasonable parameter settings. On the experimental side, we show that our algorithm ensures fast practical convergence for standard federated tasks.

PopSGD: Decentralized Stochastic Gradient Descent in the Population Model

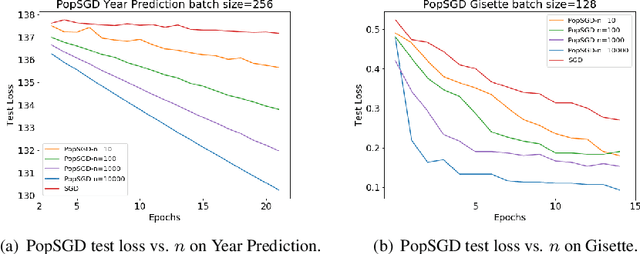
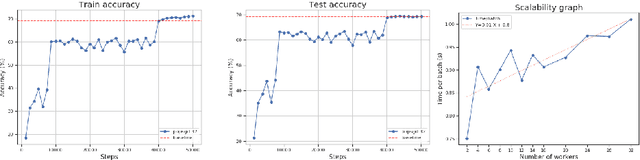
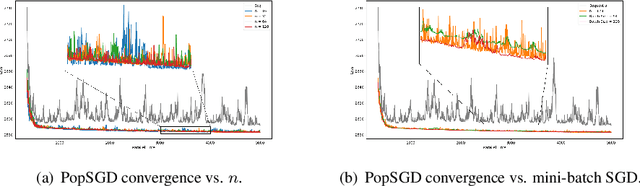
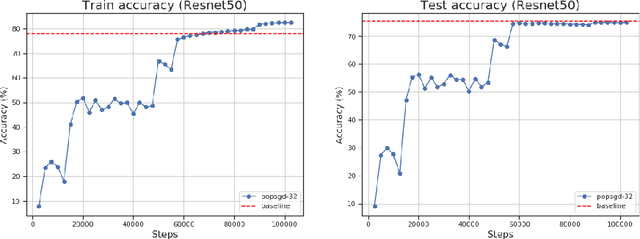
The population model is a standard way to represent large-scale decentralized distributed systems, in which agents with limited computational power interact in randomly chosen pairs, in order to collectively solve global computational tasks. In contrast with synchronous gossip models, nodes are anonymous, lack a common notion of time, and have no control over their scheduling. In this paper, we examine whether large-scale distributed optimization can be performed in this extremely restrictive setting. We introduce and analyze a natural decentralized variant of stochastic gradient descent (SGD), called PopSGD, in which every node maintains a local parameter, and is able to compute stochastic gradients with respect to this parameter. Every pair-wise node interaction performs a stochastic gradient step at each agent, followed by averaging of the two models. We prove that, under standard assumptions, SGD can converge even in this extremely loose, decentralized setting, for both convex and non-convex objectives. Moreover, surprisingly, in the former case, the algorithm can achieve linear speedup in the number of nodes $n$. Our analysis leverages a new technical connection between decentralized SGD and randomized load-balancing, which enables us to tightly bound the concentration of node parameters. We validate our analysis through experiments, showing that PopSGD can achieve convergence and speedup for large-scale distributed learning tasks in a supercomputing environment.