Hybrid Decentralized Optimization: First- and Zeroth-Order Optimizers Can Be Jointly Leveraged For Faster Convergence

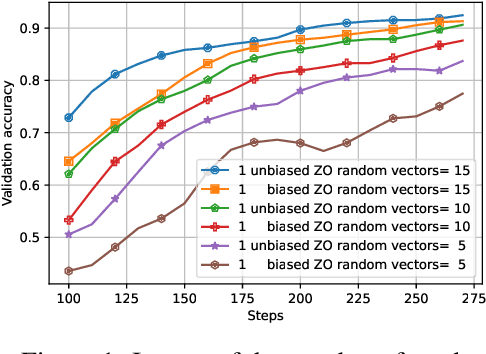
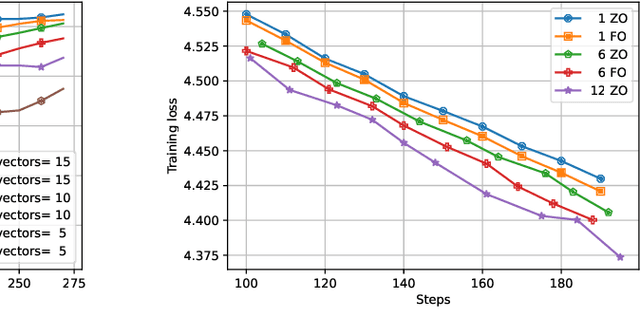
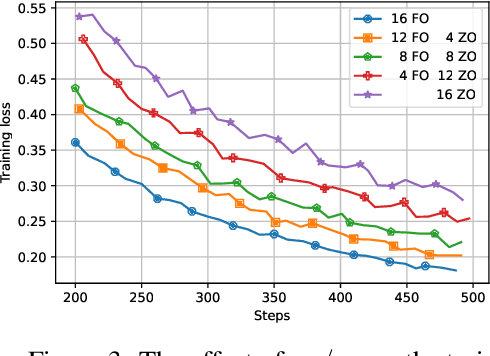
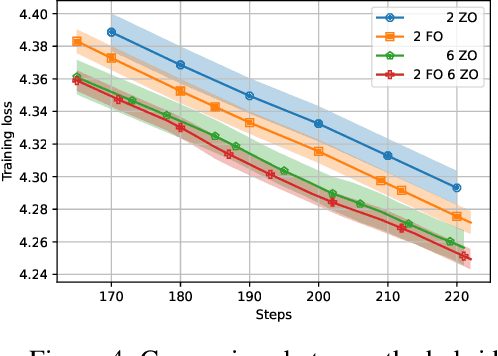
Distributed optimization has become one of the standard ways of speeding up machine learning training, and most of the research in the area focuses on distributed first-order, gradient-based methods. Yet, there are settings where some computationally-bounded nodes may not be able to implement first-order, gradient-based optimization, while they could still contribute to joint optimization tasks. In this paper, we initiate the study of hybrid decentralized optimization, studying settings where nodes with zeroth-order and first-order optimization capabilities co-exist in a distributed system, and attempt to jointly solve an optimization task over some data distribution. We essentially show that, under reasonable parameter settings, such a system can not only withstand noisier zeroth-order agents but can even benefit from integrating such agents into the optimization process, rather than ignoring their information. At the core of our approach is a new analysis of distributed optimization with noisy and possibly-biased gradient estimators, which may be of independent interest. Experimental results on standard optimization tasks confirm our analysis, showing that hybrid first-zeroth order optimization can be practical.