Align Your Flow: Scaling Continuous-Time Flow Map Distillation

Diffusion- and flow-based models have emerged as state-of-the-art generative modeling approaches, but they require many sampling steps. Consistency models can distill these models into efficient one-step generators; however, unlike flow- and diffusion-based methods, their performance inevitably degrades when increasing the number of steps, which we show both analytically and empirically. Flow maps generalize these approaches by connecting any two noise levels in a single step and remain effective across all step counts. In this paper, we introduce two new continuous-time objectives for training flow maps, along with additional novel training techniques, generalizing existing consistency and flow matching objectives. We further demonstrate that autoguidance can improve performance, using a low-quality model for guidance during distillation, and an additional boost can be achieved by adversarial finetuning, with minimal loss in sample diversity. We extensively validate our flow map models, called Align Your Flow, on challenging image generation benchmarks and achieve state-of-the-art few-step generation performance on both ImageNet 64x64 and 512x512, using small and efficient neural networks. Finally, we show text-to-image flow map models that outperform all existing non-adversarially trained few-step samplers in text-conditioned synthesis.

Cosmos-Drive-Dreams: Scalable Synthetic Driving Data Generation with World Foundation Models

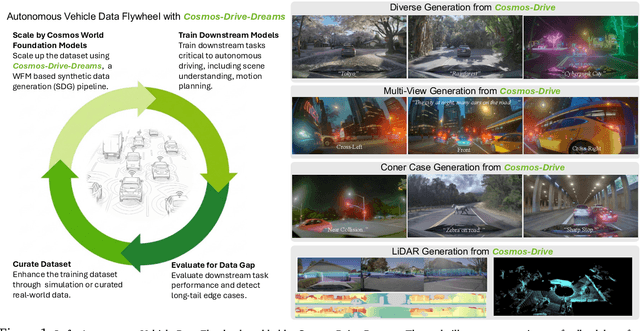
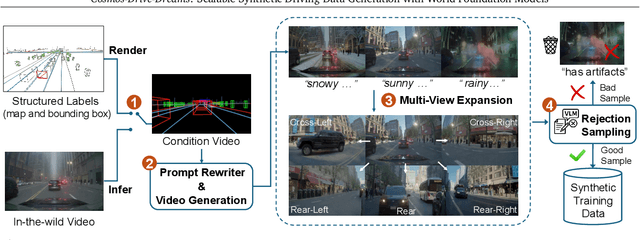
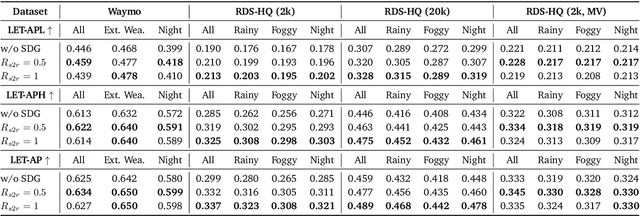
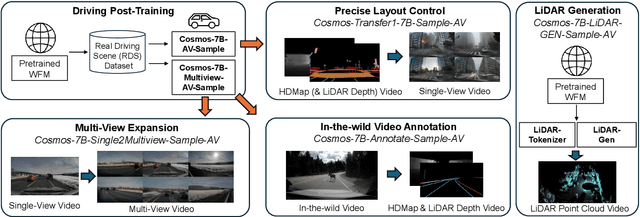
Collecting and annotating real-world data for safety-critical physical AI systems, such as Autonomous Vehicle (AV), is time-consuming and costly. It is especially challenging to capture rare edge cases, which play a critical role in training and testing of an AV system. To address this challenge, we introduce the Cosmos-Drive-Dreams - a synthetic data generation (SDG) pipeline that aims to generate challenging scenarios to facilitate downstream tasks such as perception and driving policy training. Powering this pipeline is Cosmos-Drive, a suite of models specialized from NVIDIA Cosmos world foundation model for the driving domain and are capable of controllable, high-fidelity, multi-view, and spatiotemporally consistent driving video generation. We showcase the utility of these models by applying Cosmos-Drive-Dreams to scale the quantity and diversity of driving datasets with high-fidelity and challenging scenarios. Experimentally, we demonstrate that our generated data helps in mitigating long-tail distribution problems and enhances generalization in downstream tasks such as 3D lane detection, 3D object detection and driving policy learning. We open source our pipeline toolkit, dataset and model weights through the NVIDIA's Cosmos platform. Project page: https://research.nvidia.com/labs/toronto-ai/cosmos_drive_dreams

VideoPanda: Video Panoramic Diffusion with Multi-view Attention

High resolution panoramic video content is paramount for immersive experiences in Virtual Reality, but is non-trivial to collect as it requires specialized equipment and intricate camera setups. In this work, we introduce VideoPanda, a novel approach for synthesizing 360$^\circ$ videos conditioned on text or single-view video data. VideoPanda leverages multi-view attention layers to augment a video diffusion model, enabling it to generate consistent multi-view videos that can be combined into immersive panoramic content. VideoPanda is trained jointly using two conditions: text-only and single-view video, and supports autoregressive generation of long-videos. To overcome the computational burden of multi-view video generation, we randomly subsample the duration and camera views used during training and show that the model is able to gracefully generalize to generating more frames during inference. Extensive evaluations on both real-world and synthetic video datasets demonstrate that VideoPanda generates more realistic and coherent 360$^\circ$ panoramas across all input conditions compared to existing methods. Visit the project website at https://research-staging.nvidia.com/labs/toronto-ai/VideoPanda/ for results.

Align Your Steps: Optimizing Sampling Schedules in Diffusion Models

Diffusion models (DMs) have established themselves as the state-of-the-art generative modeling approach in the visual domain and beyond. A crucial drawback of DMs is their slow sampling speed, relying on many sequential function evaluations through large neural networks. Sampling from DMs can be seen as solving a differential equation through a discretized set of noise levels known as the sampling schedule. While past works primarily focused on deriving efficient solvers, little attention has been given to finding optimal sampling schedules, and the entire literature relies on hand-crafted heuristics. In this work, for the first time, we propose a general and principled approach to optimizing the sampling schedules of DMs for high-quality outputs, called $\textit{Align Your Steps}$. We leverage methods from stochastic calculus and find optimal schedules specific to different solvers, trained DMs and datasets. We evaluate our novel approach on several image, video as well as 2D toy data synthesis benchmarks, using a variety of different samplers, and observe that our optimized schedules outperform previous hand-crafted schedules in almost all experiments. Our method demonstrates the untapped potential of sampling schedule optimization, especially in the few-step synthesis regime.

EmerDiff: Emerging Pixel-level Semantic Knowledge in Diffusion Models

Diffusion models have recently received increasing research attention for their remarkable transfer abilities in semantic segmentation tasks. However, generating fine-grained segmentation masks with diffusion models often requires additional training on annotated datasets, leaving it unclear to what extent pre-trained diffusion models alone understand the semantic relations of their generated images. To address this question, we leverage the semantic knowledge extracted from Stable Diffusion (SD) and aim to develop an image segmentor capable of generating fine-grained segmentation maps without any additional training. The primary difficulty stems from the fact that semantically meaningful feature maps typically exist only in the spatially lower-dimensional layers, which poses a challenge in directly extracting pixel-level semantic relations from these feature maps. To overcome this issue, our framework identifies semantic correspondences between image pixels and spatial locations of low-dimensional feature maps by exploiting SD's generation process and utilizes them for constructing image-resolution segmentation maps. In extensive experiments, the produced segmentation maps are demonstrated to be well delineated and capture detailed parts of the images, indicating the existence of highly accurate pixel-level semantic knowledge in diffusion models.

CCGG: A Deep Autoregressive Model for Class-Conditional Graph Generation

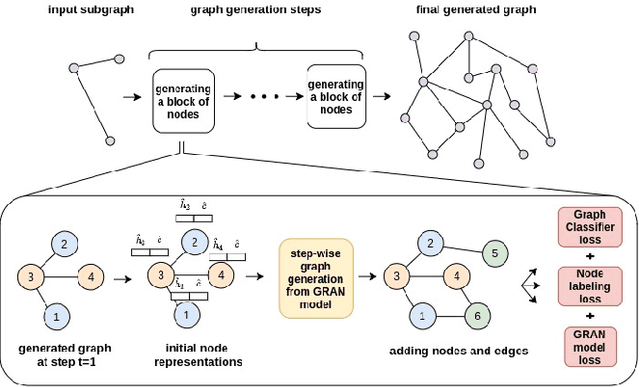
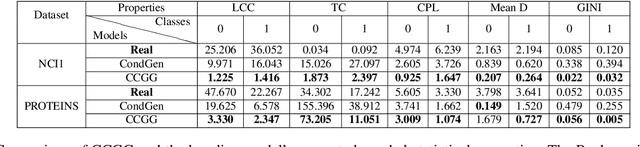
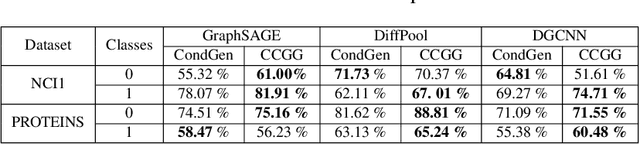
Graph data structures are fundamental for studying connected entities. With an increase in the number of applications where data is represented as graphs, the problem of graph generation has recently become a hot topic in many signal processing areas. However, despite its significance, conditional graph generation that creates graphs with desired features is relatively less explored in previous studies. This paper addresses the problem of class-conditional graph generation that uses class labels as generation constraints by introducing the Class Conditioned Graph Generator (CCGG). We built CCGG by adding the class information as an additional input to a graph generator model and including a classification loss in its total loss along with a gradient passing trick. Our experiments show that CCGG outperforms existing conditional graph generation methods on various datasets. It also manages to maintain the quality of the generated graphs in terms of distribution-based evaluation metrics.

PopSGD: Decentralized Stochastic Gradient Descent in the Population Model

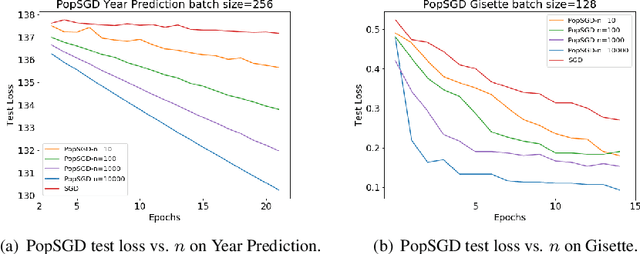
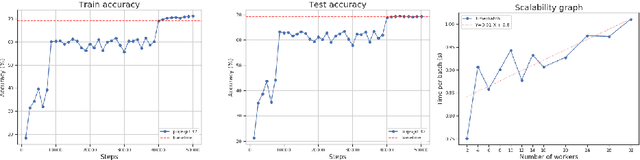
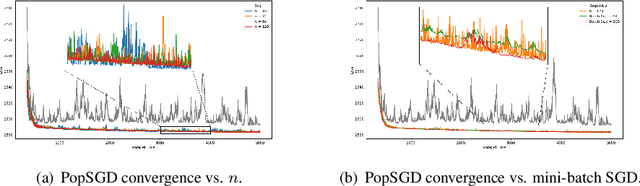
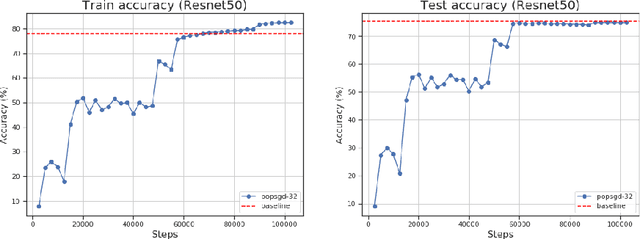
The population model is a standard way to represent large-scale decentralized distributed systems, in which agents with limited computational power interact in randomly chosen pairs, in order to collectively solve global computational tasks. In contrast with synchronous gossip models, nodes are anonymous, lack a common notion of time, and have no control over their scheduling. In this paper, we examine whether large-scale distributed optimization can be performed in this extremely restrictive setting. We introduce and analyze a natural decentralized variant of stochastic gradient descent (SGD), called PopSGD, in which every node maintains a local parameter, and is able to compute stochastic gradients with respect to this parameter. Every pair-wise node interaction performs a stochastic gradient step at each agent, followed by averaging of the two models. We prove that, under standard assumptions, SGD can converge even in this extremely loose, decentralized setting, for both convex and non-convex objectives. Moreover, surprisingly, in the former case, the algorithm can achieve linear speedup in the number of nodes $n$. Our analysis leverages a new technical connection between decentralized SGD and randomized load-balancing, which enables us to tightly bound the concentration of node parameters. We validate our analysis through experiments, showing that PopSGD can achieve convergence and speedup for large-scale distributed learning tasks in a supercomputing environment.