Derivative-based regularization for regression
Paper and Code
May 01, 2024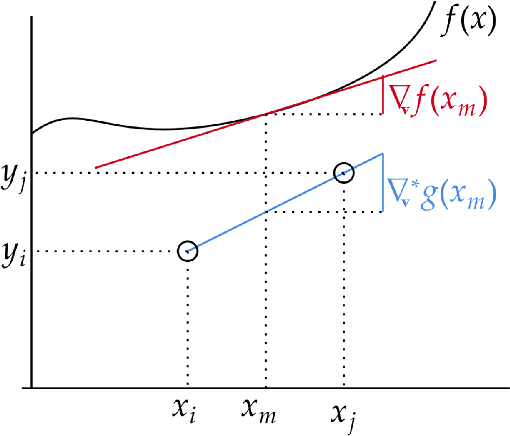
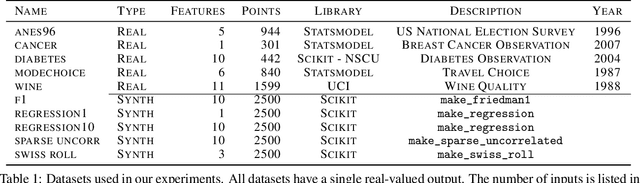
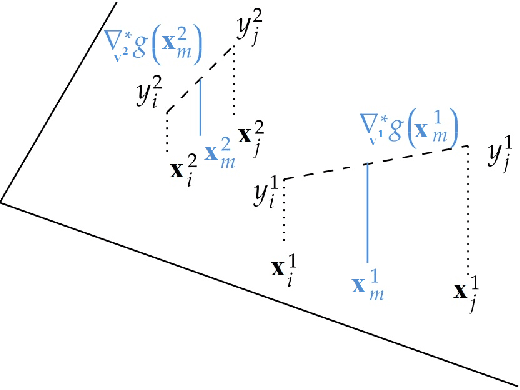

In this work, we introduce a novel approach to regularization in multivariable regression problems. Our regularizer, called DLoss, penalises differences between the model's derivatives and derivatives of the data generating function as estimated from the training data. We call these estimated derivatives data derivatives. The goal of our method is to align the model to the data, not only in terms of target values but also in terms of the derivatives involved. To estimate data derivatives, we select (from the training data) 2-tuples of input-value pairs, using either nearest neighbour or random, selection. On synthetic and real datasets, we evaluate the effectiveness of adding DLoss, with different weights, to the standard mean squared error loss. The experimental results show that with DLoss (using nearest neighbour selection) we obtain, on average, the best rank with respect to MSE on validation data sets, compared to no regularization, L2 regularization, and Dropout.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge