Learning big logical rules by joining small rules

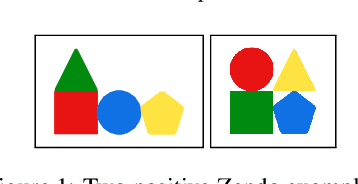
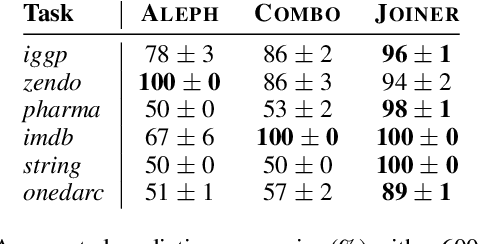
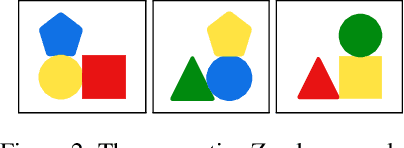
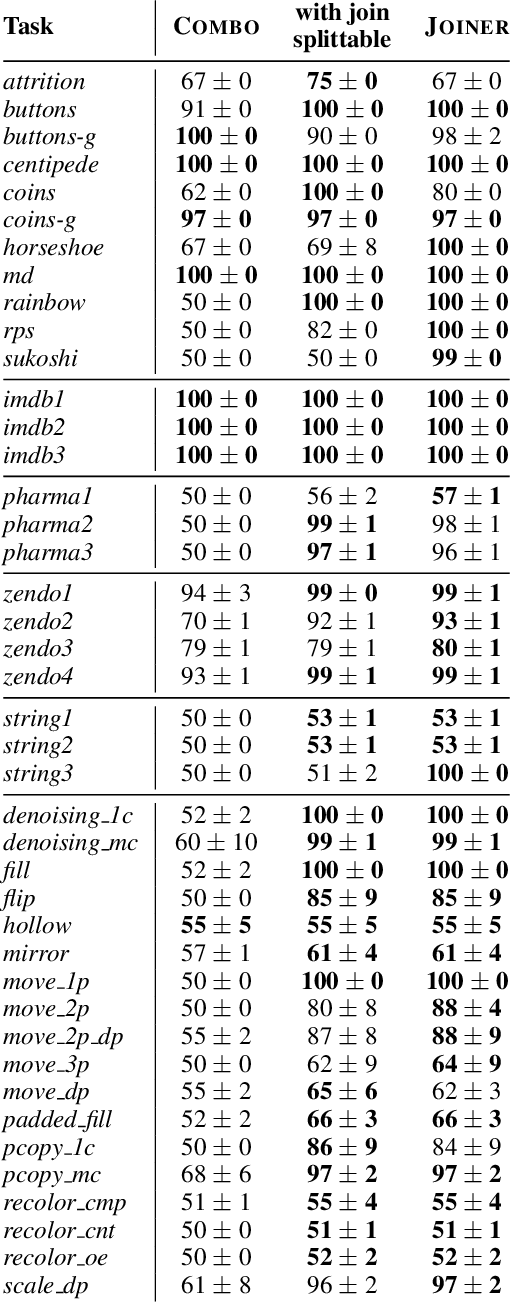
A major challenge in inductive logic programming is learning big rules. To address this challenge, we introduce an approach where we join small rules to learn big rules. We implement our approach in a constraint-driven system and use constraint solvers to efficiently join rules. Our experiments on many domains, including game playing and drug design, show that our approach can (i) learn rules with more than 100 literals, and (ii) drastically outperform existing approaches in terms of predictive accuracies.

Parallel Constraint-Driven Inductive Logic Programming

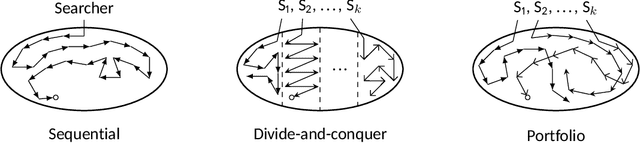
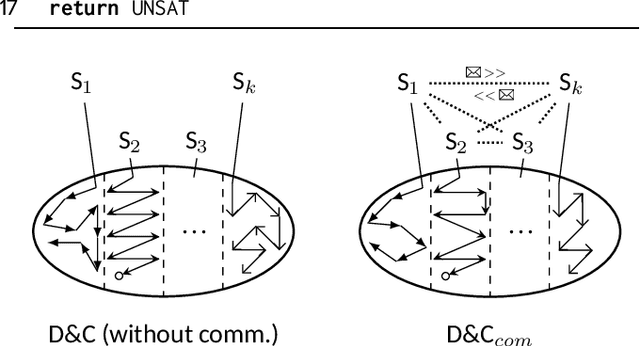
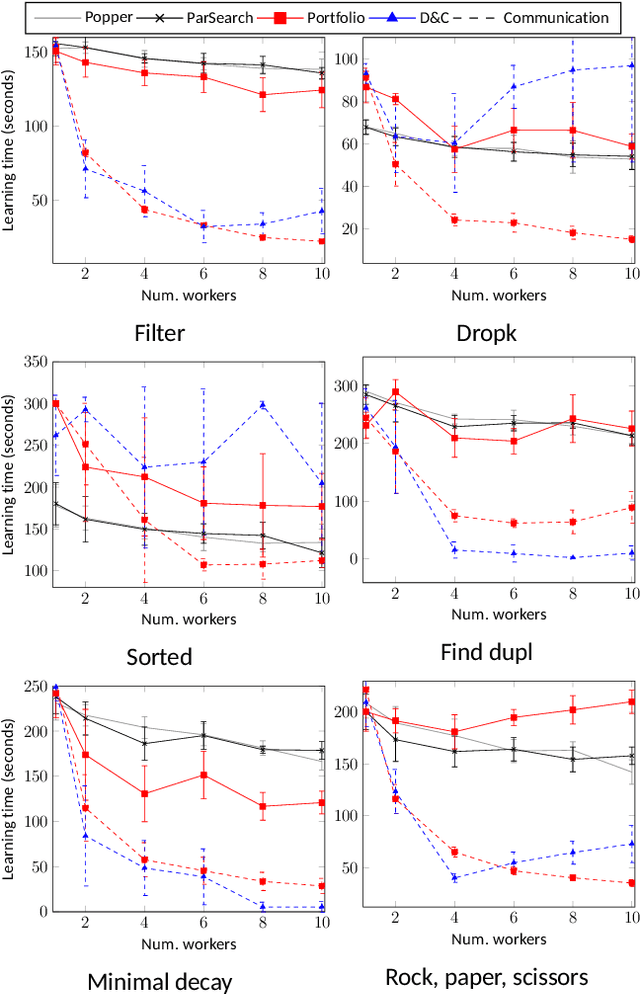
Multi-core machines are ubiquitous. However, most inductive logic programming (ILP) approaches use only a single core, which severely limits their scalability. To address this limitation, we introduce parallel techniques based on constraint-driven ILP where the goal is to accumulate constraints to restrict the hypothesis space. Our experiments on two domains (program synthesis and inductive general game playing) show that (i) parallelisation can substantially reduce learning times, and (ii) worker communication (i.e. sharing constraints) is important for good performance.

Predicate Invention by Learning From Failures

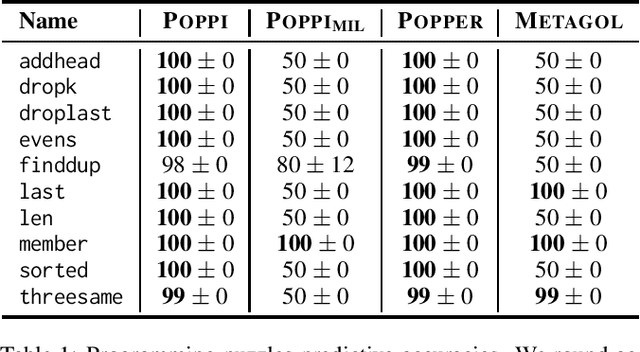
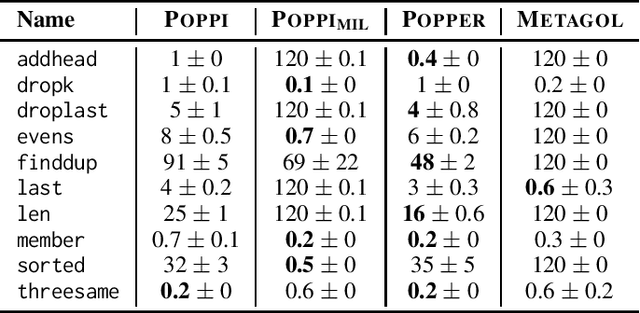
Discovering novel high-level concepts is one of the most important steps needed for human-level AI. In inductive logic programming (ILP), discovering novel high-level concepts is known as predicate invention (PI). Although seen as crucial since the founding of ILP, PI is notoriously difficult and most ILP systems do not support it. In this paper, we introduce POPPI, an ILP system that formulates the PI problem as an answer set programming problem. Our experiments show that (i) PI can drastically improve learning performance when useful, (ii) PI is not too costly when unnecessary, and (iii) POPPI can substantially outperform existing ILP systems.

Learning Logic Programs by Explaining Failures

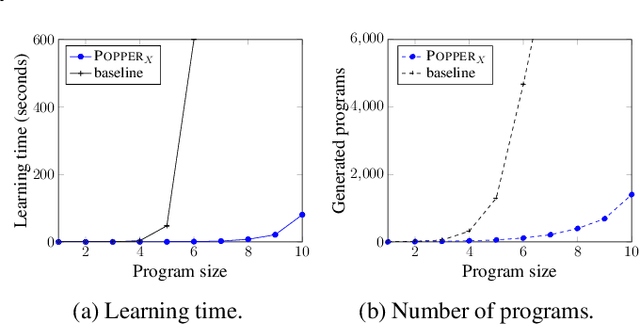
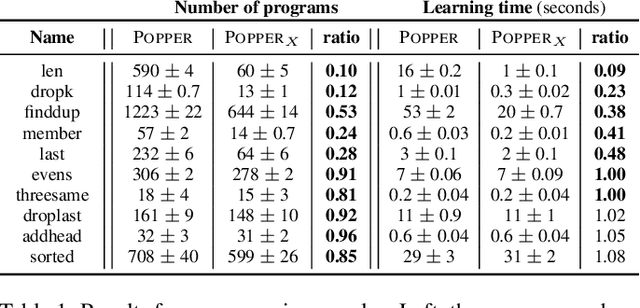
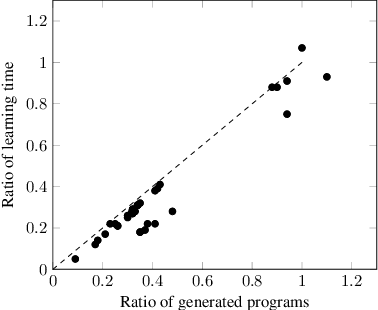
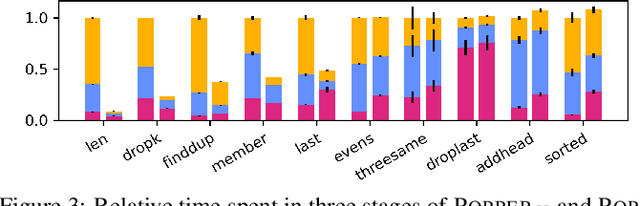
Scientists form hypotheses and experimentally test them. If a hypothesis fails (is refuted), scientists try to explain the failure to eliminate other hypotheses. We introduce similar explanation techniques for inductive logic programming (ILP). We build on the ILP approach learning from failures. Given a hypothesis represented as a logic program, we test it on examples. If a hypothesis fails, we identify clauses and literals responsible for the failure. By explaining failures, we can eliminate other hypotheses that will provably fail. We introduce a technique for failure explanation based on analysing SLD-trees. We experimentally evaluate failure explanation in the Popper ILP system. Our results show that explaining failures can drastically reduce learning times.

Refinement Type Directed Search for Meta-Interpretive-Learning of Higher-Order Logic Programs

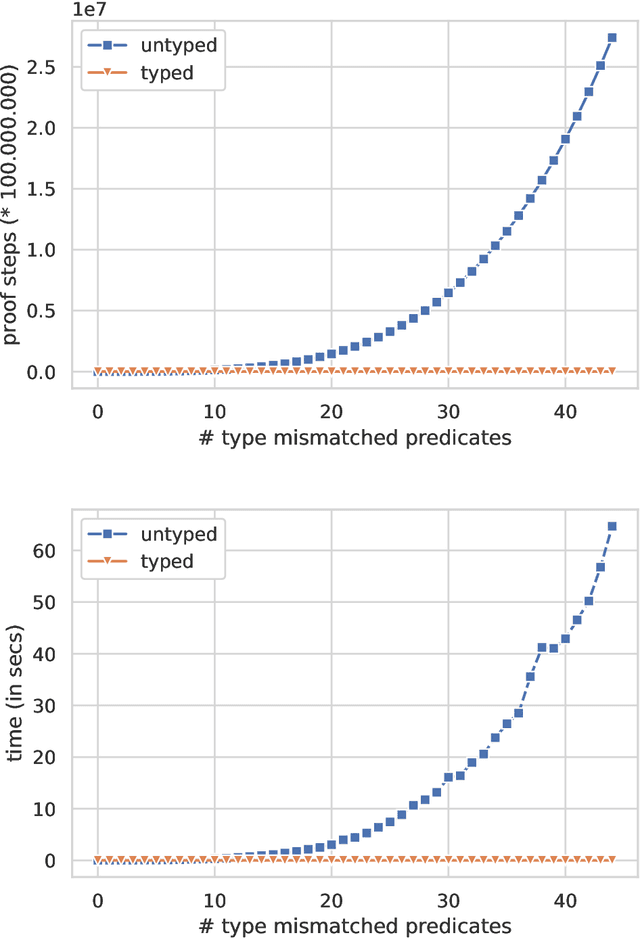
The program synthesis problem within the Inductive Logic Programming (ILP) community has typically been seen as untyped. We consider the benefits of user provided types on background knowledge. Building on the Meta-Interpretive Learning (MIL) framework, we show that type checking is able to prune large parts of the hypothesis space of programs. The introduction of polymorphic type checking to the MIL approach to logic program synthesis is validated by strong theoretical and experimental results, showing a cubic reduction in the size of the search space and synthesis time, in terms of the number of typed background predicates. Additionally we are able to infer polymorphic types of synthesized clauses and of entire programs. The other advancement is in developing an approach to leveraging refinement types in ILP. Here we show that further pruning of the search space can be achieved, though the SMT solving used for refinement type checking comes

Learning programs by learning from failures

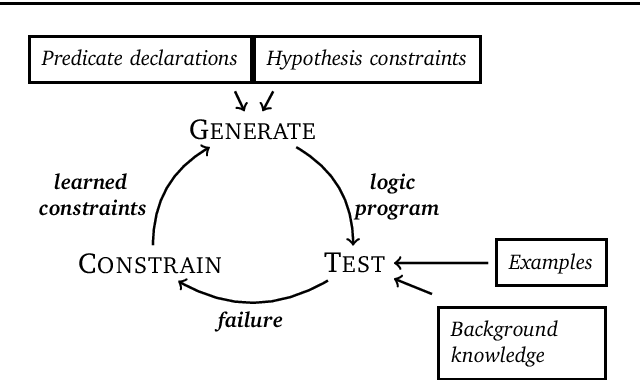
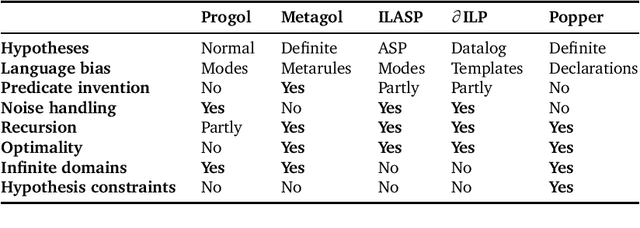
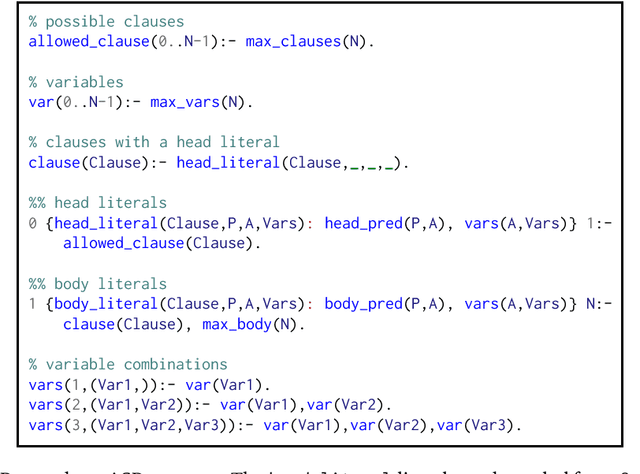
We introduce learning programs by learning from failures. In this approach, an inductive logic programming (ILP) system (the learner) decomposes the learning problem into three separate stages: generate, test, and constrain. In the generate stage, the learner generates a hypothesis (a logic program) that satisfies a set of hypothesis constraints (constraints on the syntactic form of hypotheses). In the test stage, the learner tests the hypothesis against training examples. A hypothesis fails when it does not entail all the positive examples or entails a negative example. If a hypothesis fails, then, in the constrain stage, the learner learns constraints from the failed hypothesis to prune the hypothesis space, i.e. to constrain subsequent hypothesis generation. For instance, if a hypothesis is too general (entails a negative example), the constraints prune generalisations of the hypothesis. If a hypothesis is too specific (does not entail all the positive examples), the constraints prune specialisations of the hypothesis. This loop repeats until (1) the learner finds a hypothesis that entails all the positive and none of the negative examples, or (2) there are no more hypotheses to test. We implement our idea in Popper, an ILP system which combines answer set programming and Prolog. Popper supports infinite domains, reasoning about lists and numbers, learning optimal (textually minimal) programs, and learning recursive programs. Our experimental results on three diverse domains (number theory problems, robot strategies, and list transformations) show that (1) constraints drastically improve learning performance, and (2) Popper can substantially outperform state-of-the-art ILP systems, both in terms of predictive accuracies and learning times.

Learning higher-order logic programs

A key feature of inductive logic programming (ILP) is its ability to learn first-order programs, which are intrinsically more expressive than propositional programs. In this paper, we introduce techniques to learn higher-order programs. Specifically, we extend meta-interpretive learning (MIL) to support learning higher-order programs by allowing for \emph{higher-order definitions} to be used as background knowledge. Our theoretical results show that learning higher-order programs, rather than first-order programs, can reduce the textual complexity required to express programs which in turn reduces the size of the hypothesis space and sample complexity. We implement our idea in two new MIL systems: the Prolog system \namea{} and the ASP system \nameb{}. Both systems support learning higher-order programs and higher-order predicate invention, such as inventing functions for \tw{map/3} and conditions for \tw{filter/3}. We conduct experiments on four domains (robot strategies, chess playing, list transformations, and string decryption) that compare learning first-order and higher-order programs. Our experimental results support our theoretical claims and show that, compared to learning first-order programs, learning higher-order programs can significantly improve predictive accuracies and reduce learning times.