Relational decomposition for program synthesis

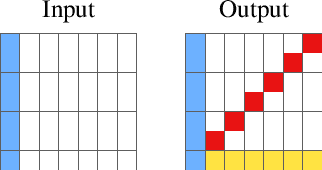
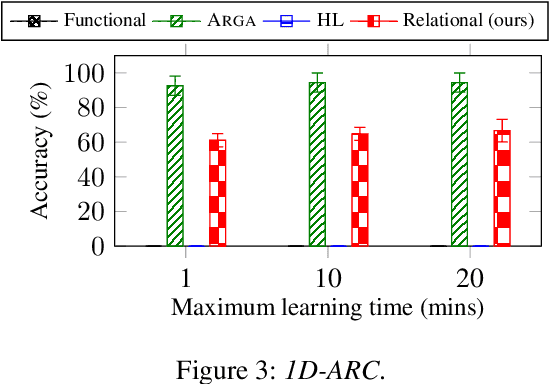
We introduce a novel approach to program synthesis that decomposes complex functional tasks into simpler relational synthesis sub-tasks. We demonstrate the effectiveness of our approach using an off-the-shelf inductive logic programming (ILP) system on three challenging datasets. Our results show that (i) a relational representation can outperform a functional one, and (ii) an off-the-shelf ILP system with a relational encoding can outperform domain-specific approaches.

Can humans teach machines to code?

The goal of inductive program synthesis is for a machine to automatically generate a program from user-supplied examples of the desired behaviour of the program. A key underlying assumption is that humans can provide examples of sufficient quality to teach a concept to a machine. However, as far as we are aware, this assumption lacks both empirical and theoretical support. To address this limitation, we explore the question `Can humans teach machines to code?'. To answer this question, we conduct a study where we ask humans to generate examples for six programming tasks, such as finding the maximum element of a list. We compare the performance of a program synthesis system trained on (i) human-provided examples, (ii) randomly sampled examples, and (iii) expert-provided examples. Our results show that, on most of the tasks, non-expert participants did not provide sufficient examples for a program synthesis system to learn an accurate program. Our results also show that non-experts need to provide more examples than both randomly sampled and expert-provided examples.

Learning logic programs by finding minimal unsatisfiable subprograms

The goal of inductive logic programming (ILP) is to search for a logic program that generalises training examples and background knowledge. We introduce an ILP approach that identifies minimal unsatisfiable subprograms (MUSPs). We show that finding MUSPs allows us to efficiently and soundly prune the search space. Our experiments on multiple domains, including program synthesis and game playing, show that our approach can reduce learning times by 99%.

Learning big logical rules by joining small rules

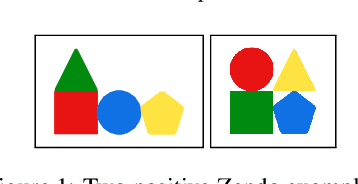
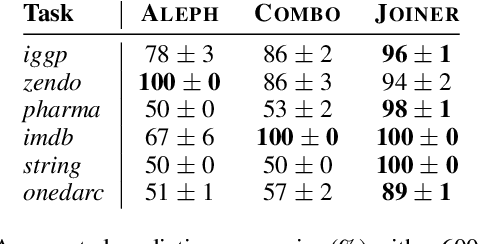
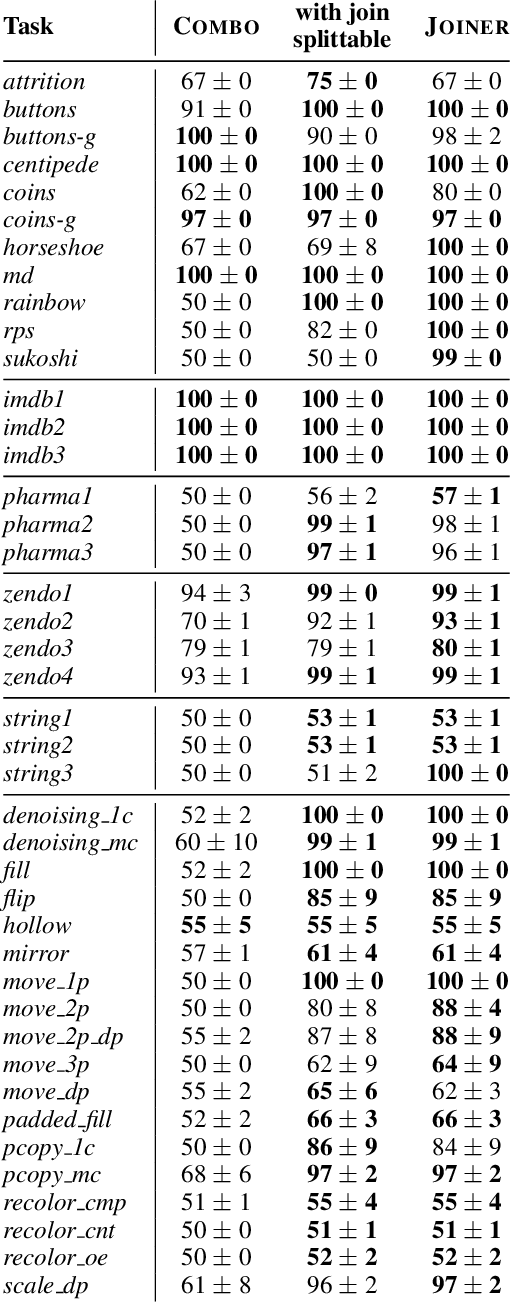
A major challenge in inductive logic programming is learning big rules. To address this challenge, we introduce an approach where we join small rules to learn big rules. We implement our approach in a constraint-driven system and use constraint solvers to efficiently join rules. Our experiments on many domains, including game playing and drug design, show that our approach can (i) learn rules with more than 100 literals, and (ii) drastically outperform existing approaches in terms of predictive accuracies.

Learning MDL logic programs from noisy data

Many inductive logic programming approaches struggle to learn programs from noisy data. To overcome this limitation, we introduce an approach that learns minimal description length programs from noisy data, including recursive programs. Our experiments on several domains, including drug design, game playing, and program synthesis, show that our approach can outperform existing approaches in terms of predictive accuracies and scale to moderate amounts of noise.

Learning Logic Programs by Discovering Higher-Order Abstractions

Discovering novel abstractions is important for human-level AI. We introduce an approach to discover higher-order abstractions, such as map, filter, and fold. We focus on inductive logic programming, which induces logic programs from examples and background knowledge. We introduce the higher-order refactoring problem, where the goal is to compress a logic program by introducing higher-order abstractions. We implement our approach in STEVIE, which formulates the higher-order refactoring problem as a constraint optimisation problem. Our experimental results on multiple domains, including program synthesis and visual reasoning, show that, compared to no refactoring, STEVIE can improve predictive accuracies by 27% and reduce learning times by 47%. We also show that STEVIE can discover abstractions that transfer to different domains

Relational program synthesis with numerical reasoning

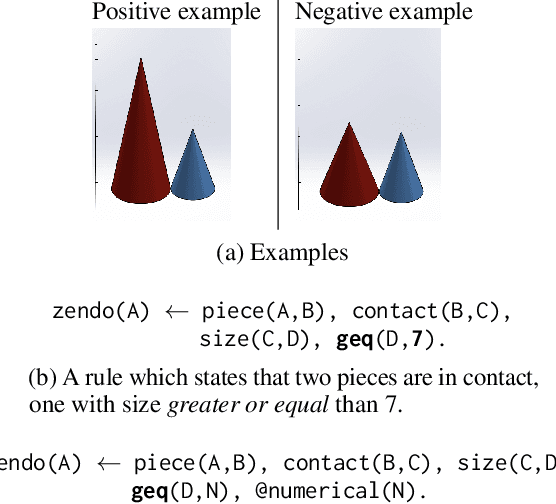
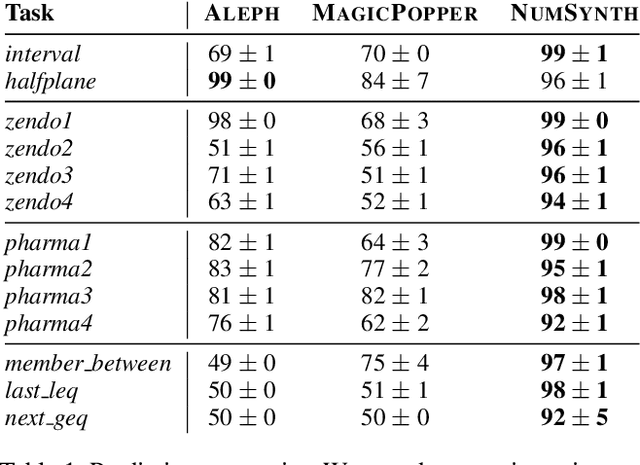
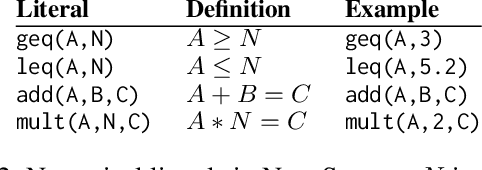
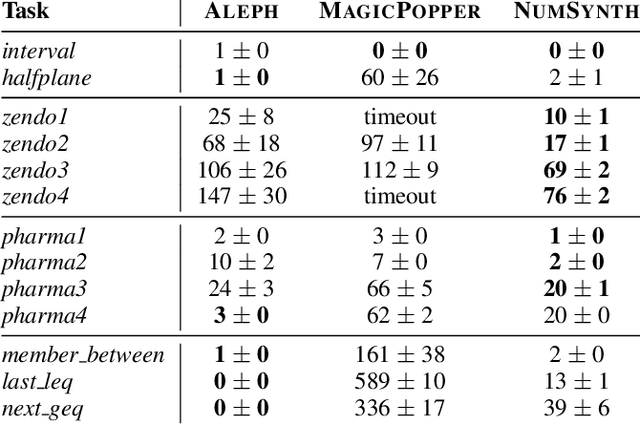
Program synthesis approaches struggle to learn programs with numerical values. An especially difficult problem is learning continuous values over multiple examples, such as intervals. To overcome this limitation, we introduce an inductive logic programming approach which combines relational learning with numerical reasoning. Our approach, which we call NUMSYNTH, uses satisfiability modulo theories solvers to efficiently learn programs with numerical values. Our approach can identify numerical values in linear arithmetic fragments, such as real difference logic, and from infinite domains, such as real numbers or integers. Our experiments on four diverse domains, including game playing and program synthesis, show that our approach can (i) learn programs with numerical values from linear arithmetical reasoning, and (ii) outperform existing approaches in terms of predictive accuracies and learning times.

Learning programs with magic values

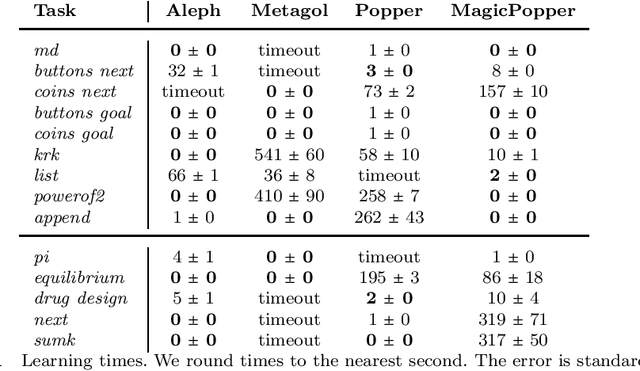
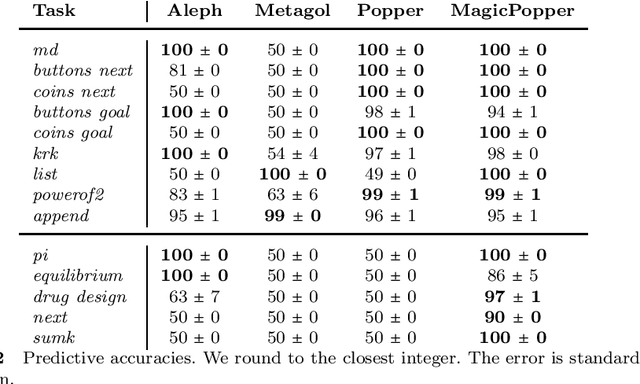
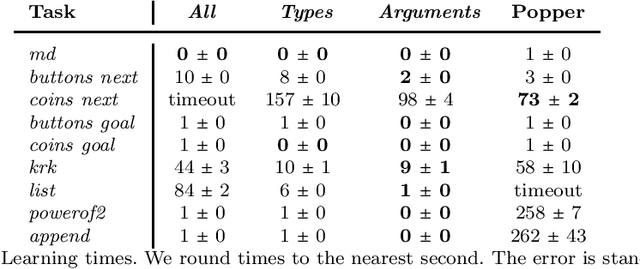
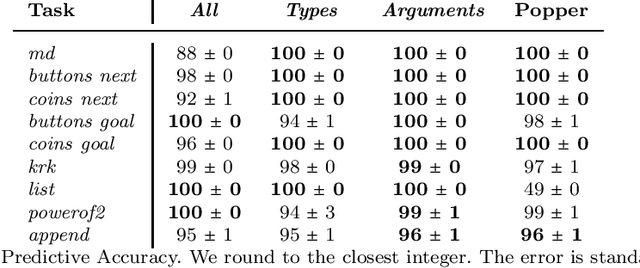
A magic value in a program is a constant symbol that is essential for the execution of the program but has no clear explanation for its choice. Learning programs with magic values is difficult for existing program synthesis approaches. To overcome this limitation, we introduce an inductive logic programming approach to efficiently learn programs with magic values. Our experiments on diverse domains, including program synthesis, drug design, and game playing, show that our approach can (i) outperform existing approaches in terms of predictive accuracies and learning times, (ii) learn magic values from infinite domains, such as the value of pi, and (iii) scale to domains with millions of constant symbols.

Learning logic programs by discovering where not to search

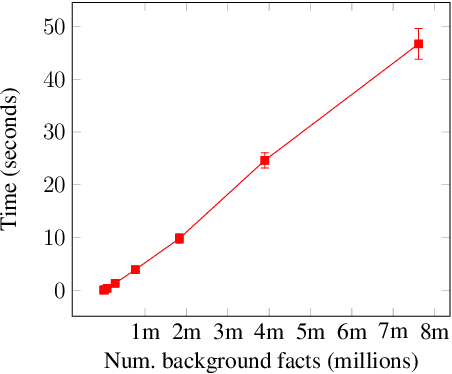
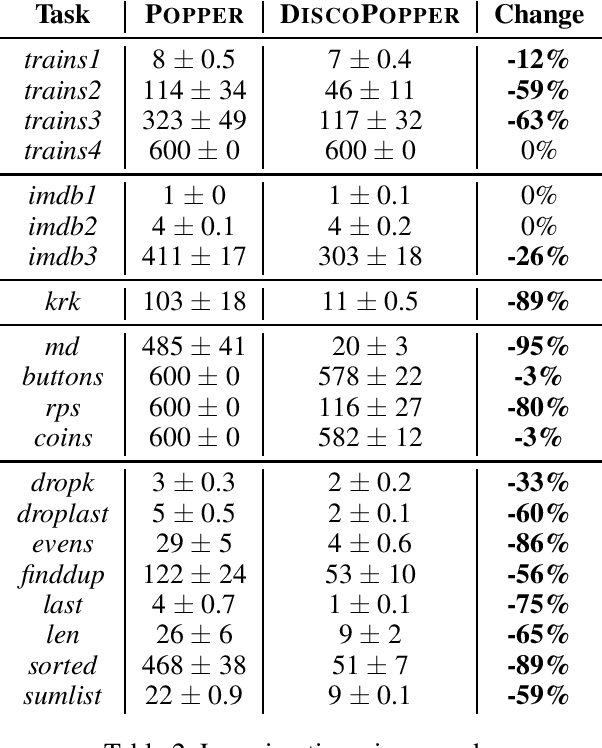
The goal of inductive logic programming (ILP) is to search for a hypothesis that generalises training examples and background knowledge (BK). To improve performance, we introduce an approach that, before searching for a hypothesis, first discovers `where not to search'. We use given BK to discover constraints on hypotheses, such as that a number cannot be both even and odd. We use the constraints to bootstrap a constraint-driven ILP system. Our experiments on multiple domains (including program synthesis and inductive general game playing) show that our approach can substantially reduce learning times.

Beneficial and Harmful Explanatory Machine Learning

Given the recent successes of Deep Learning in AI there has been increased interest in the role and need for explanations in machine learned theories. A distinct notion in this context is that of Michie's definition of Ultra-Strong Machine Learning (USML). USML is demonstrated by a measurable increase in human performance of a task following provision to the human of a symbolic machine learned theory for task performance. A recent paper demonstrates the beneficial effect of a machine learned logic theory for a classification task, yet no existing work has examined the potential harmfulness of machine's involvement in human learning. This paper investigates the explanatory effects of a machine learned theory in the context of simple two person games and proposes a framework for identifying the harmfulness of machine explanations based on the Cognitive Science literature. The approach involves a cognitive window consisting of two quantifiable bounds and it is supported by empirical evidence collected from human trials. Our quantitative and qualitative results indicate that human learning aided by a symbolic machine learned theory which satisfies a cognitive window has achieved significantly higher performance than human self learning. Results also demonstrate that human learning aided by a symbolic machine learned theory that fails to satisfy this window leads to significantly worse performance than unaided human learning.