Relational program synthesis with numerical reasoning
Paper and Code
Oct 04, 2022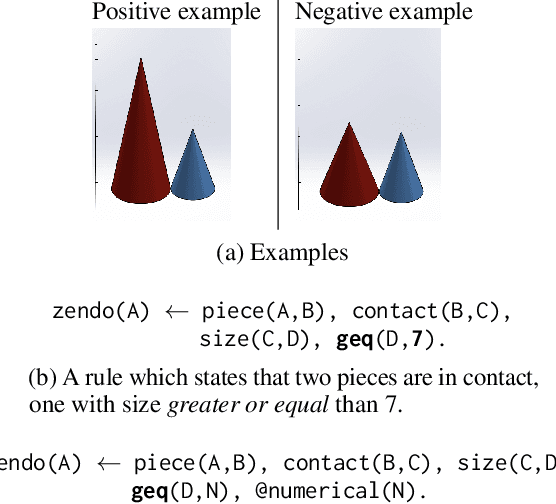
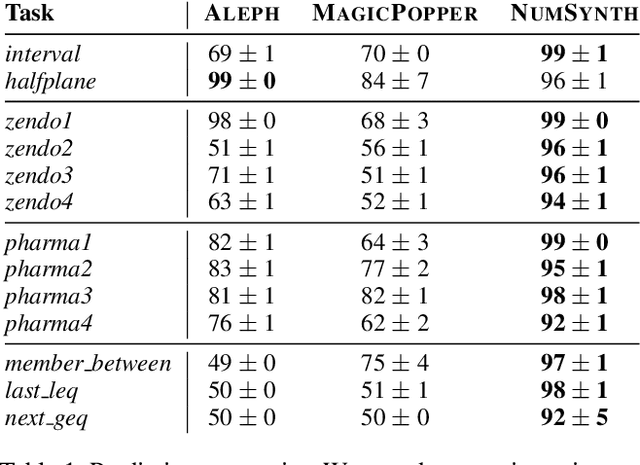
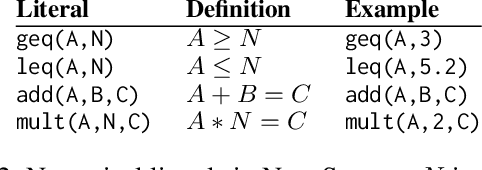
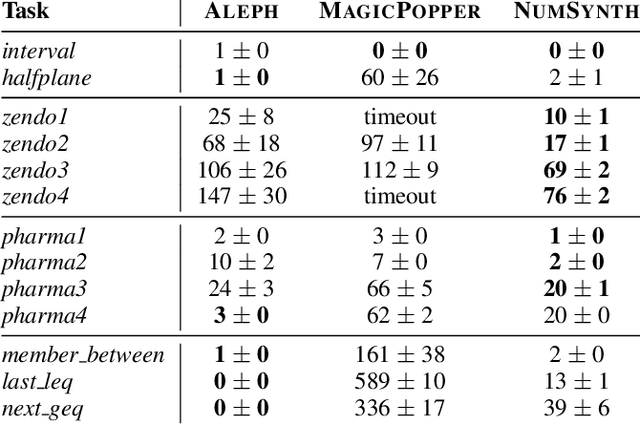
Program synthesis approaches struggle to learn programs with numerical values. An especially difficult problem is learning continuous values over multiple examples, such as intervals. To overcome this limitation, we introduce an inductive logic programming approach which combines relational learning with numerical reasoning. Our approach, which we call NUMSYNTH, uses satisfiability modulo theories solvers to efficiently learn programs with numerical values. Our approach can identify numerical values in linear arithmetic fragments, such as real difference logic, and from infinite domains, such as real numbers or integers. Our experiments on four diverse domains, including game playing and program synthesis, show that our approach can (i) learn programs with numerical values from linear arithmetical reasoning, and (ii) outperform existing approaches in terms of predictive accuracies and learning times.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge