Marijn Heule
Symbiosis of Search and Heuristics for Random 3-SAT
Feb 18, 2014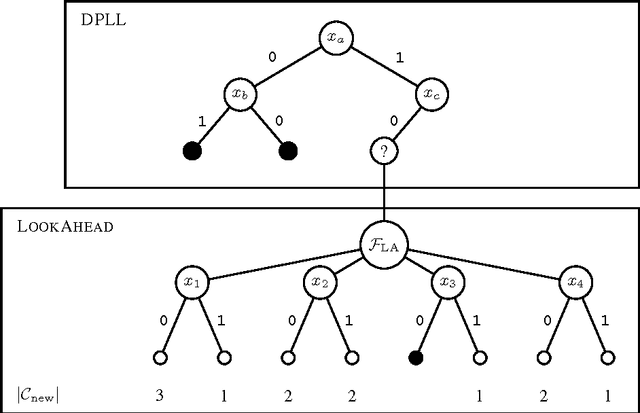
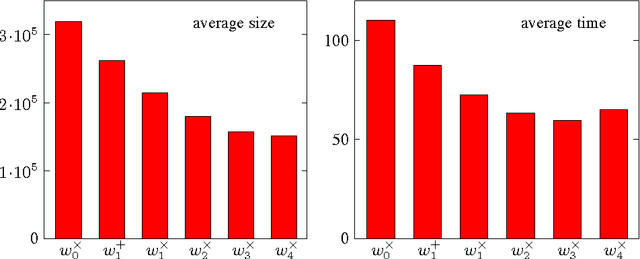
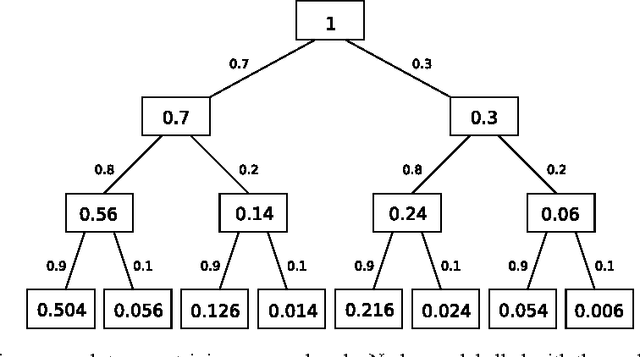
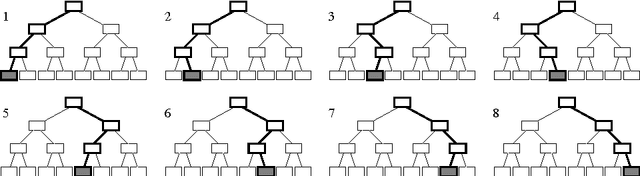
Abstract:When combined properly, search techniques can reveal the full potential of sophisticated branching heuristics. We demonstrate this observation on the well-known class of random 3-SAT formulae. First, a new branching heuristic is presented, which generalizes existing work on this class. Much smaller search trees can be constructed by using this heuristic. Second, we introduce a variant of discrepancy search, called ALDS. Theoretical and practical evidence support that ALDS traverses the search tree in a near-optimal order when combined with the new heuristic. Both techniques, search and heuristic, have been implemented in the look-ahead solver march. The SAT 2009 competition results show that march is by far the strongest complete solver on random k-SAT formulae.
Towards Ultra Rapid Restarts
Feb 18, 2014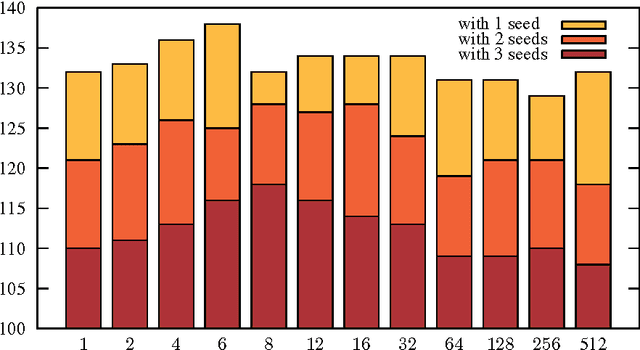
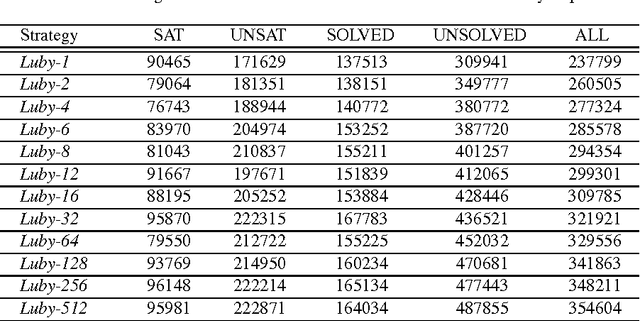
Abstract:We observe a trend regarding restart strategies used in SAT solvers. A few years ago, most state-of-the-art solvers restarted on average after a few thousands of backtracks. Currently, restarting after a dozen backtracks results in much better performance. The main reason for this trend is that heuristics and data structures have become more restart-friendly. We expect further continuation of this trend, so future SAT solvers will restart even more rapidly. Additionally, we present experimental results to support our observations.
Covered Clause Elimination
Nov 23, 2010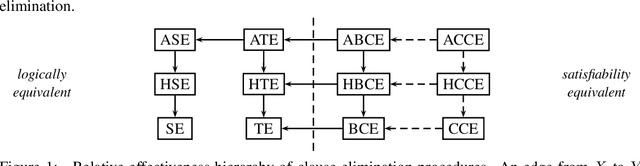
Abstract:Generalizing the novel clause elimination procedures developed in [M. Heule, M. J\"arvisalo, and A. Biere. Clause elimination procedures for CNF formulas. In Proc. LPAR-17, volume 6397 of LNCS, pages 357-371. Springer, 2010.], we introduce explicit (CCE), hidden (HCCE), and asymmetric (ACCE) variants of a procedure that eliminates covered clauses from CNF formulas. We show that these procedures are more effective in reducing CNF formulas than the respective variants of blocked clause elimination, and may hence be interesting as new preprocessing/simplification techniques for SAT solving.
* 5 pages
Symmetry within Solutions
Apr 15, 2010Abstract:We define the concept of an internal symmetry. This is a symmety within a solution of a constraint satisfaction problem. We compare this to solution symmetry, which is a mapping between different solutions of the same problem. We argue that we may be able to exploit both types of symmetry when finding solutions. We illustrate the potential of exploiting internal symmetries on two benchmark domains: Van der Waerden numbers and graceful graphs. By identifying internal symmetries we are able to extend the state of the art in both cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge