Pseudo-Boolean Proof Logging for Optimal Classical Planning

We introduce lower-bound certificates for classical planning tasks, which can be used to prove the unsolvability of a task or the optimality of a plan in a way that can be verified by an independent third party. We describe a general framework for generating lower-bound certificates based on pseudo-Boolean constraints, which is agnostic to the planning algorithm used. As a case study, we show how to modify the $A^{*}$ algorithm to produce proofs of optimality with modest overhead, using pattern database heuristics and $h^\textit{max}$ as concrete examples. The same proof logging approach works for any heuristic whose inferences can be efficiently expressed as reasoning over pseudo-Boolean constraints.

Certified MaxSAT Preprocessing

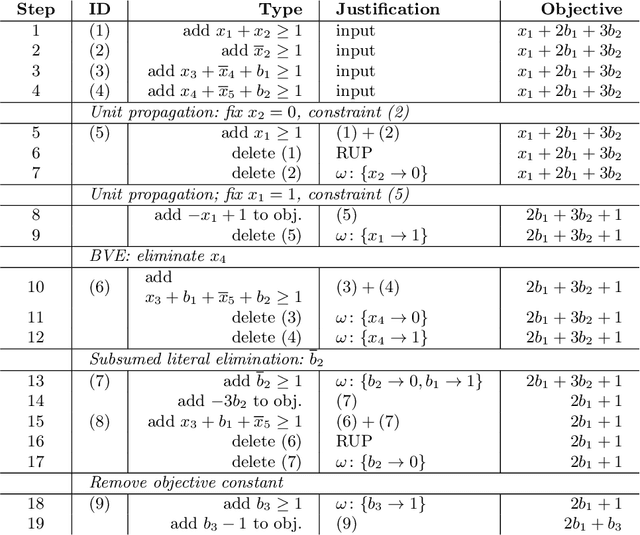
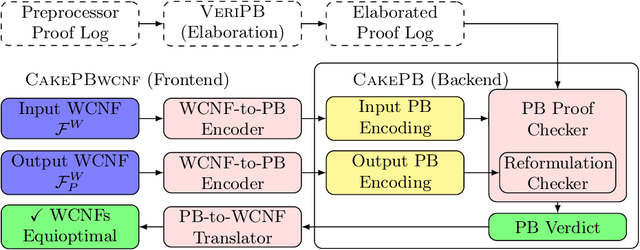
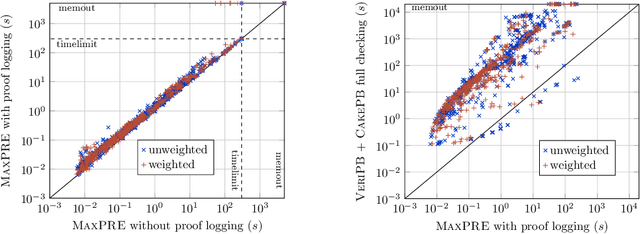
Building on the progress in Boolean satisfiability (SAT) solving over the last decades, maximum satisfiability (MaxSAT) has become a viable approach for solving NP-hard optimization problems, but ensuring correctness of MaxSAT solvers has remained an important concern. For SAT, this is largely a solved problem thanks to the use of proof logging, meaning that solvers emit machine-verifiable proofs of (un)satisfiability to certify correctness. However, for MaxSAT, proof logging solvers have started being developed only very recently. Moreover, these nascent efforts have only targeted the core solving process, ignoring the preprocessing phase where input problem instances can be substantially reformulated before being passed on to the solver proper. In this work, we demonstrate how pseudo-Boolean proof logging can be used to certify the correctness of a wide range of modern MaxSAT preprocessing techniques. By combining and extending the VeriPB and CakePB tools, we provide formally verified, end-to-end proof checking that the input and preprocessed output MaxSAT problem instances have the same optimal value. An extensive evaluation on applied MaxSAT benchmarks shows that our approach is feasible in practice.

Certified Symmetry and Dominance Breaking for Combinatorial Optimisation

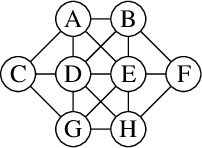
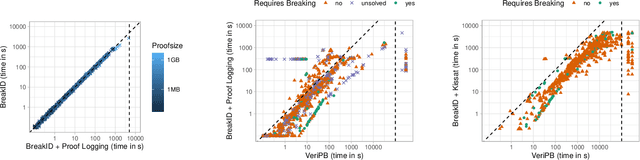
Symmetry and dominance breaking can be crucial for solving hard combinatorial search and optimisation problems, but the correctness of these techniques sometimes relies on subtle arguments. For this reason, it is desirable to produce efficient, machine-verifiable certificates that solutions have been computed correctly. Building on the cutting planes proof system, we develop a certification method for optimisation problems in which symmetry and dominance breaking are easily expressible. Our experimental evaluation demonstrates that we can efficiently verify fully general symmetry breaking in Boolean satisfiability (SAT) solving, thus providing, for the first time, a unified method to certify a range of advanced SAT techniques that also includes XOR and cardinality reasoning. In addition, we apply our method to maximum clique solving and constraint programming as a proof of concept that the approach applies to a wider range of combinatorial problems.

Planning with Learned Binarized Neural Networks Benchmarks for MaxSAT Evaluation 2021

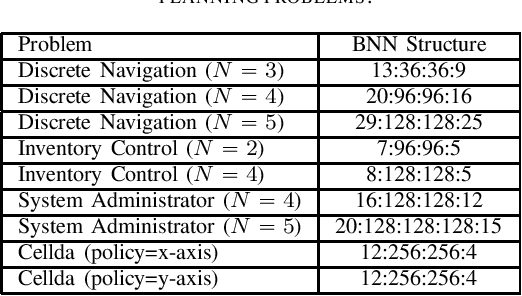
This document provides a brief introduction to learned automated planning problem where the state transition function is in the form of a binarized neural network (BNN), presents a general MaxSAT encoding for this problem, and describes the four domains, namely: Navigation, Inventory Control, System Administrator and Cellda, that are submitted as benchmarks for MaxSAT Evaluation 2021.